[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters
[单位]:浙大fastlab
[作者]:汪哲培、周鑫、许超、高飞
[期刊]:2022TRO
摘要:我们提出了一个基于优化的多旋翼飞行器轨迹规划框架,该框架受几何空间约束和用户定义的动力学约束。该框架的基础是一个新的轨迹表示,它建立在我们新的无约束控制代价最小化的最优性条件之上。我们在这种轨迹表示上设计了线性复杂度运算,以便在各种规划要求下进行时空变形。平滑映射用于以轻量级的方式精确消除几何约束。通过解耦稠密约束评估和稀疏参量化,以及平坦映射的后向微分,可以支持大范围的状态输入约束。因此,该框架将一个普遍受限的多旋翼规划问题转化为一个可以可靠高效地求解的无约束优化问题。对于资源和机动能力有限的多旋翼飞行器,我们的框架弥补了解决方案质量、规划频率和约束保真度之间的差距。其通用性和鲁棒性在不同任务的应用和实验中得到了验证。还进行了大量的仿真和基准测试,以展示其生成高质量解决方案的能力,同时保证有与其他专用方法相比的快上一个数量级的计算速度。
关键词:非完整运动规划,空中机器人,自主智能体
目录
1.引言:
2.相关工作:
2.1 微分平坦多旋翼
2.2 基于采样的运动规划
2.3 基于优化的运动规划
3.准备条件:
3.1 微分平坦
3.2 在平坦输出空间中直接优化
3.3 问题列出
4.多阶段Multistage控制代价最小化:
4.1 无约束控制代价最小化
4.2 优化条件
4.3 无代价函数最小化
4.4 带时空变形的MINCO轨迹
5.几何约束飞行轨迹优化:
5.1 时间约束消除
5.2 空间约束消除
5.3 时间曲线惩罚函数
5.4 无约束非线性规划--轨迹优化
6.应用:
6.1 大规模无约束控制代价最小化
6.2 基于安全飞行走廊的轨迹生成
6.3 在商空间(Quotient Space)的SE(3)运动规划
编辑
7.讨论和总结:
7.1 扩展
7.2 限制
7.3 总结
8 附录
1.引言:
多旋翼飞行器依靠稳健高效的轨迹规划,在复杂环境中实现安全灵活的自主导航(Bry et al. 2015; Oleynikova et al. 2020; Zhang et al. 2020; Zhou et al. 2021)。 对于机器人来说,精确地结合动态、平滑性和安全性对于生成高质量的运动至关重要。 此外,轻量级机器人,如 SWaP(尺寸、重量和功率)约束下的多旋翼飞行器,对使用有限板载资源的实时计算提出了更高的要求。 尽管已经提出了各种成功的通用运动动力学规划或最优控制工具,但其中很少有人能保证高频在线规划,同时还考虑了对多旋翼动力学的一般约束。 因此,现有应用程序通常对轨迹过度简化以提高计算效率,从而限制了对机器能力的充分利用。
对于高性能规划,上面所提到的,拥有四个主要算法的挑战。
1)确保运动安全通常涉及与大量离散环境数据的频繁交互,这些数据具有广泛的非平滑性。
2)当多旋翼飞机在其能力极限飞行时,设备动力学的非线性给直接强制执行物理可接受的状态和输入带来了困难。
3)高质量的运动通常需要动力学过程的精细离散化,使得对任务资源的要求往往不切实际。
4)使用稀疏表示轨迹的方法缺乏一种有效的方法在满足连续时间约束的同时优化时间曲线。
在本文中,我们通过设计一个轻量级且灵活的优化框架来克服所有这些挑战,以满足基于新颖轨迹类的各种运动要求。
作为所提出框架的理论基础,我们以无约束线性动力学的一般形式为相关的多阶段控制代价最小化问题提出了最优条件。 更重要的是,首次提供了必要性和充分性的证明。 最优性条件易于使用,因为可以在时间和空间方面直接构造具有线性复杂度的唯一最优解。 因此,与传统方案相比,计算效率提高了几个数量级(Mellinger 和 Kumar 2011;Bry 等人 2015;Burke 等人 2020)。 此外,这些条件的存在性和唯一性进一步为问题参数的敏感性平滑性提供了关键信息。
为了在不牺牲解决方案质量的情况下减轻轨迹规划中的计算负担,必须使用稀疏参数化在适合系统动力学的同时保持灵活性。因此,我们基于最优性条件设计了一个新的轨迹类。这个轨迹类中的任何元素都已经是一个无约束的控制代价最小化,因此我们将其命名为MINCO(最小控制)。这种新设计的轨迹类不同于传统的样条曲线,后者主要关注几何形状的平滑度,如B样条曲线和Bezier曲线。MINCO的稀疏参数被设计用于直接控制轨迹的空间和时间曲线,这在满足多旋翼飞机动力学可行性时具有同等的重要性。具体来说,MINCO将中间点和时间向量作为紧凑表示。此外,还设计了一种时空变形方案,使得MINCO中的轨迹可以在任何用户定义的目标函数下进行优化。为了提高变形计算的效率,还提出了一种具有线性复杂度的梯度传播方案。
我们的框架基于sample-based方法或search-based方法的结果,利用低维自由空间的几何近似。通过无障碍凸基元的并集形成的配置约束来保证安全性。提出了约束消除方案,使得MINCO可以通过无约束优化自由变形。该方案在不引入额外的局部极小值的情况下,精确地消除了直接定义在决策变量上的约束。
可靠的运动规划需要允许的状态和输入,而大多数现有的基于平坦度的方法仅支持差分约束。为了确保高保真的可行性,我们提出了一种系统的方法来为我们的稀疏参数化实施用户定义的状态输入约束,而无需诉诸轨迹的精细离散化。我们利用平坦映射的向后微分,以使约束违反可以反映在其稀疏参数的梯度中。此外,还提出了一种可微惩罚函数来强制执行一般的连续时间约束。
我们的框架侧重于计算高效但高质量的轨迹规划,其中存在复杂的安全约束、动力学的关键限制以及多旋翼飞行器的特定任务要求。 为了验证其有效性,我们针对各种尖端的多旋翼轨迹规划方法进行了广泛的基准测试。 结果表明,我们的方法在效率上超过了现有方法几个数量级,并且与通用最优控制求解器保持了可比的解决方案质量。 我们还进行了多功能仿真和真实世界的实验,以展示所提出方法的实际性能。 例如,实时 SE(3) 规划使得多旋翼飞行器安全、敏捷地依次通过几个狭窄的倾斜间隙。 我们框架的稳定性和鲁棒性也通过与任意放置的gap的持久实时交互来验证。
总结本文的贡献如下:
(1):首次提出了多阶段控制代价最小化的一般形式的最优条件,并证明了必要性和充分性。(4.2部分阐述)
(2):设计了一种新的轨迹类来满足用户定义的目标,同时通过相应的形式良好的线性复杂度运算来保持局部光滑性。(4.4部分阐述)
(3):针对具有用户定义状态输入约束的多旋翼系统,提出了一种灵活的轨迹规划框架,该框架同时利用了约束消除和约束转移。(第5节阐述)
(4):一组验证我们方法的仿真和实验在效率、最优性、鲁棒性和通用性方面显著优于现有技术。(第6节阐述)
2.相关工作:
尽管现有文献中有各种多旋翼轨迹规划方法,但尚未出现一个完整的框架来完成高频大规模的规划,同时结合用户定义的在状态和控制上的连续时间约束。 对这种框架的强烈需求来自这样一个事实,即受复杂动力学约束的高质量运动需要足够的计算时间和资源。 这一要求很难满足,尤其是在轻型多旋翼飞行器的时间要求严格的飞行中。 为了弥补这一差距,我们提出了一个专门用于多旋翼飞行器的高效计算框架,同时探索和利用最优控制和运动规划的不同能力。
2.1 微分平坦多旋翼
Fliess 等人介绍了非线性系统的微分平坦度的概念。(1995 年)并在机器人轨迹规划中引起了极大的关注(Van Nieuwstadt 和 Murray 1998 年;Martin 等人 2003 年;Ryu 和 Agrawal 2011 年)。 这一特性使得从平坦空间中输出的有限阶导数中恢复平面系统的完整状态和输入成为可能。 至于多旋翼飞行器,Mellinger 和 Kumar (2011) 证明了带有对齐螺旋桨的常规四旋翼飞行器的微分平坦,它以三维扭矩和推力作为输入。 他们利用平坦空间来生成满足微分约束的轨迹并计算跟踪控制器的前馈项。 穆勒等人 (2015) 表明简化动力学的平坦度足以生成四轴飞行器轨迹,其中以机身角速率和推力作为输入。 费林等人 (2011) 显示了六轴飞行器的平面度,其输入是所需的方向和总推力。它们利用线性二次型调节器 (LQR) 线性化系统时的公称状态和输入。费斯勒等人(2018年)考虑更复杂的系统动力学和空气动力学效应,设计高速轻型控制器。线性旋翼阻力效应通过线性加速度和角加速度并入平移部分和旋转部分。他们进一步展示了受旋翼阻力影响的多旋翼系统的平坦度。 此外,Mu 和 Chirarattananon (2019) 研究了带有倾斜螺旋桨的欠驱动多旋翼飞行器。 他们证明,只要满足输入秩条件,平坦度适用于各种三轴飞行器、四轴飞行器和六轴飞行器。
多旋翼系统的平坦空间(如果成立)有利于轨迹生成和跟踪,因为可以以代数方法来计算参考状态和输入。 基于这一性质,上述文献直接消除了系统动力学中的微分约束。 然而,常用的微分约束仅被认为在具有可接受控制输入的状态空间的特定区域中有效。 因此,对状态和控制的约束对于确保考虑真实物理系统的可行性很重要。 本文提出的框架也是基于多旋翼飞行器的平坦空间,但与以前的工作不同,正式考虑了通用形式的状态输入约束并灵活处理。
2.2 基于采样的运动规划
基于采样的运动规划具有在解空间中探索和开发的性质。它非常适合于寻求非凸问题的全局解,而非凸问题的复杂性主要来源于配置空间。概率路线图(PRM)(Kavraki et al.1996)从静态配置空间中随机抽样的可行顶点构造一个无障碍图,用于多个最短路径查询。Rapidlyexploring随机树(RRT)(LaValle 1998)通过基于单个查询信息的在线采样,以增量方式构建树。它们都是概率完全的(Kavraki et al.1998;Frazzoli et al.2002),因为随着样本数趋于无穷大,它们的失效概率呈指数衰减为零。一个里程碑是Karaman和Frazzoli(2011)分析了基于采样的算法的渐近最优性条件。他们还提出了PRM和RRT的渐近最优变体,称为PRM*和RRT*。当样本数趋于无穷大时,这些变量确保收敛到全局最优解。如果提供基于系统动力学的转向功能,它们在运动动力学规划(或轨迹规划)问题中也有成功的应用(LaValle and Kuffner Jr 2001;Frazzoli et al.2002;Karaman and Frazzoli 2010)。还有一些算法(Janson等人2015;Li等人2016;Gammell等人2018)进一步探索了随机运动规划的效率或适用性。
当机器人具有许多自由度 (DoF) 并且配置空间高度非凸时,基于最佳采样的规划器是有希望的,尽管很耗时。 所提出的框架不会同时面临来自配置空间和多旋翼动力学的困难。 它利用基于采样的能力来克服环境的复杂性。对于局部自由空间的几何近似,仅需要低维无碰撞路径。然后,我们的框架完成了与路径同调的运动的优化。它旨在明确地结合系统状态输入约束,这不是基于采样的方法的优势。通过这种方式,环境和动力学的复杂性分别在前端和后端进行划分和解决。(也就是说,前端解决环境的复杂性,后端解决动力学的复杂性)。
2.3 基于优化的运动规划
基于优化的规划器通常专注于运动规划问题的局部解决方案,其中指定了目标或最优标准。 因此,它们通常建立在特定的环境预处理方法上,以便将障碍物信息作为目标或约束编码到优化中。
轨迹优化被认为是一个最优控制问题,在控制界对一般动力学系统进行了广泛的研究(Betts 1998)。有多种通用解算器能够计算出高质量的解,例如基于shooting的解算器ACADO(Houska等人,2011年)和基于配置的解算器one GPOPS-II(Patterson和Rao,2014年)。通过这些方法,最初的优化通常被离散化,并转化为非线性规划(NLP),然后通过完善的NLP方法进行求解,如SNOPT(Gill et al.2005)或IPOPT(W¨achter and Biegler 2006)。然而,机器人运动规划可能会施加难以建模的约束、非光滑性,甚至整数变量。此外,通用方法通常需要较长的计算时间,因此不适合时间关键型应用。例如,Bry等人(2015年)报告称,对于在圆柱形障碍物中飞行的12状态飞机,使用SNOPT的直接配置(DC)需要几分钟来优化4.5m的轨迹(Barry等人,2014年)。因此,需要专门的方法来克服这些困难。
对于微分平坦多旋翼飞行器,在足够平滑的前提下,运动规划实际上可以转化为低维优化。Mellinger和Kumar【11】使用固定时间的样条曲线来表示四旋翼直升机的轨迹。二次规划(QP)由snap的二次成本和安全的线性约束组成。 然而,需要解决扰动问题,以便可以通过有限差分来估计时间分配的梯度,并且执行器约束也被过度简化。 布赖等人 (2015)推导出由平方导数积分形成的无约束 QP 的封闭形式解。 他们启发式地从 RRT* 的可行路径添加航路点以计算解决方案,直到满足安全性。 这种方法无疑是有效的,但不能保证在障碍物丰富的环境中获得高质量的解决方案。 此外,该方法需要对矩阵求逆,但未讨论矩阵的非奇异性。 Deits 和 Tedrake (2015b) 使用多面体来近似自由空间。 如果每条轨迹完全位于多面体内部,则每条轨迹的安全性等同于平方和 (SOS) 条件。 由于区间分配,他们通过混合整数二阶锥规划 (MISOCP) 求解轨迹。 该方法在计算时间不可接受的情况下生成全局最优轨迹。 高等人(2020)也使用多面体形自由空间表示。 它们交替优化轨迹的几何和时间分布。 安全性由贝塞尔曲线的凸包属性强制执行,动态曲线通过时间最优路径参数化 (TOPP) 进行优化。 还有一些变体提出了对上述方法的改进。 例如,Tordesillas 等人(2019 年)通过以保守性为代价(Tordesillas 和 How 2020)用对 Bezier 曲线具有线性约束的多项式替换 SOS 条件来提高该方法的效率(Deits 和 Tedrake 2015b)。 孙等人(2020)通过优化时间分配来进一步消除其整数变量,其中梯度是根据双层优化的敏感性估计的。
上述针对多旋翼的专门方法利用连续时间参数化,例如样条曲线或贝塞尔曲线,来克服精细离散化带来的计算负担。 然而,这种参数化提出了现有方法中未解决的其他问题。 首先,表示的时间分配或区间分配都缺乏针对不同场景的有效且灵活的优化方案。 其次,对于现有的轨迹表示,强制执行连续时间的可行性要么是昂贵的,要么是保守的。 第三,非线性多旋翼系统的动态限制只能通过限制轨迹导数的范数来启发式地实现。 相比之下,结合高保真动力学的方法没有这些问题(Ryou et al. 2020; Foehn and Scaramuzza 2020),而它们的高质量解决方案需要大量的计算资源并且只能离线应用。 在本文中,也提出了稀疏轨迹表示,它通过引入统一的技术有效地解决了这些先前存在的缺点。此外,轨迹质量与通用最优控制求解器的轨迹质量相当。
3.准备条件:
3.1 微分平坦
其中![]() :
:![]() ,
,![]() :
:![]() ,状态
,状态![]() 假设映射
假设映射![]() 的秩为 m。 如果存在由 x 和 u 的有限导数确定的平坦输出
的秩为 m。 如果存在由 x 和 u 的有限导数确定的平坦输出![]() ,则称该系统是微分平坦的 [7],这样 x 和 u 都可以通过 z 的有限导数进行参数化:
,则称该系统是微分平坦的 [7],这样 x 和 u 都可以通过 z 的有限导数进行参数化:
其中 Ψx:![]() 和Ψu:
和Ψu:![]() 都是由
都是由![]() 和
和![]() 导出。直观地说,状态和控制可以从 z 确定,而无需显式结合系统动力学 (1)。
导出。直观地说,状态和控制可以从 z 确定,而无需显式结合系统动力学 (1)。
利用系统的平坦度,当(1)中只有微分约束时,轨迹生成很方便。 如果我们引入一个新的控制变量![]() 并且定义
并且定义![]() 为:
为:
输入![]() 然后将原始平面系统精确地线性化为 m 个解耦的 s 积分器链。 让
然后将原始平面系统精确地线性化为 m 个解耦的 s 积分器链。 让![]() 表示 z 中的第 i 个,
表示 z 中的第 i 个,![]() 表示 v 中的第 i 个。第i阶积分链表示为
表示 v 中的第 i 个。第i阶积分链表示为
其中![]() 和
和![]() 分别是具有适当size的全零矩阵和单位矩阵。提供初始状态和目标状态,可以代数计算每个积分器链(7)的边界值。满足边界条件,从这些 m阶积分器链集成的任何轨迹都可以通过以下变换 (2) 和 (3) 转换为原始平面系统的可行轨迹 (Van Nieuwstadt 和 Murray 1998)。
分别是具有适当size的全零矩阵和单位矩阵。提供初始状态和目标状态,可以代数计算每个积分器链(7)的边界值。满足边界条件,从这些 m阶积分器链集成的任何轨迹都可以通过以下变换 (2) 和 (3) 转换为原始平面系统的可行轨迹 (Van Nieuwstadt 和 Murray 1998)。
对于具有较小 m 的动力学,平坦映射 Ψx 和 Ψu 进一步减小了轨迹维度并消除了微分约束 (1),如图 2 所示。作为副作用,当原始系统的 x 和 u 上存在约束时,来自 Ψx 和 Ψu 的非线性会给 z 的轨迹生成带来额外的困难。 然而,如果平坦输出空间与相关规划问题的配置空间一致,这种影响就会大大减轻。
图2.平坦系统的变换 Ψu 和 Ψx 消除了状态输入空间(左坐标)中动态的微分约束(蓝色表面)。原始状态输入约束 D(红色区域)也被转换为平面输出空间(右坐标)中的新约束 (蓝色体积)。
3.2 在平坦输出空间中直接优化
幸运的是,对多旋翼机的微分性进行了很好的研究,结果表明它具有与相关配置空间重叠的物理意义上的输出空间。由Mellinger和Kumar研究(2011);费斯勒等人 (2018);Mu和Chirarattananon(2019年),许多欠驱动多旋翼具有以下输出:
其中(Px,Py,Pz)是重心的平移,![]() 是yaw角。 平坦输出z,尤其是其平动部分,对具有复杂空间约束的平坦空间中多旋翼飞行器的运动规划提供了很多方便。
是yaw角。 平坦输出z,尤其是其平动部分,对具有复杂空间约束的平坦空间中多旋翼飞行器的运动规划提供了很多方便。
为了给多旋翼飞行器生成可行的运动,我们优化了平坦输出空间中的轨迹 z(t):[0, T]→![]() ,以便直接强制执行大多数空间约束。然后,平坦映射
,以便直接强制执行大多数空间约束。然后,平坦映射![]() 和
和![]() 被用于变换z(t)到状态输入轨迹
被用于变换z(t)到状态输入轨迹![]() 和
和![]() 。
。
对于轨迹平滑度,我们采用时间正则化的二次控制代价 (Verriest and Lewis 1991) 作为 z(t) 上的代价函数。 为了可行性,我们将多旋翼系统的一般约束分为两部分。 第一部分由来自配置空间的空间约束组成。 通常,无碰撞运动意味着:
其中 F 是配置空间中有关的无障碍区域。 第二部分包括对状态和系统动力学控制的任何其他约束,例如作动器限制或特定任务的约束。 第二部分中的所有这些用户定义的约束都表示为
显然,通过平坦性,对x和u的约束在 z(t) 的有限导数上具有等价形式。 为简单起见,我们将 式(9) 表示为 ![]()
其中包含![]() 个等效约束。
个等效约束。
值得注意的是,我们没有对多旋翼动力学和平坦映射做进一步的假设。 换句话说,所提出的框架支持广泛的多旋翼飞行器,包括但不限于[11]-[15]中的多旋翼飞行器。
3.3 问题列出
总结上述描述会给出以下问题:
![]()
其中![]() 是具有正元素的对角矩阵。
是具有正元素的对角矩阵。![]() 是时间正则化项。
是时间正则化项。![]() 是起始条件,
是起始条件,![]() 是终止条件。积分器链的控制量
是终止条件。积分器链的控制量![]() 允许在有限数量的时刻不连续,正如现有文献 (Bertsekas 1995) 中通常假设的那样。
允许在有限数量的时刻不连续,正如现有文献 (Bertsekas 1995) 中通常假设的那样。
因为连续时间非线性约束和非凸集约束F,在(11)中的轨迹优化是非平凡的。我们指定了一些合理的条件,使其成为一个定义良好的问题。至于时间正则化ρ,它在控制代价和总时间期望之间进行权衡,
![]()
其中![]() 是正值,通常情况是
是正值,通常情况是![]() 或
或![]() 带着期望的时间
带着期望的时间![]() 。此外,还可以定义 ρ 来严格固定总时间
。此外,还可以定义 ρ 来严格固定总时间
对于非线性约束 ,要求其为![]() ,即两次连续可微。对于配置空间中的可行域F,我们用
,即两次连续可微。对于配置空间中的可行域F,我们用![]() 闭凸集的并作为几何近似
闭凸集的并作为几何近似
为简单起见,在这些凸集上假设局部顺序连接:
其中 Int(·) 表示集合的内部。 ![]() 和
和![]() 的平移分别记在
的平移分别记在 ![]() 和
和 ![]() 中。对于
中。对于 ![]() ,我们考虑每个 Pi 是一个封闭的 m 维球的情况
,我们考虑每个 Pi 是一个封闭的 m 维球的情况
或者,更一般地,由其 H 表示 [37] 描述的有界凸多面体具有潜在的冗余约束:
对于(11)中的优化问题,我们的目标是构造一个计算效率高的解算器,同时保留处理(8)中不同任务特定约束D的灵活性。
4.多阶段Multistage控制代价最小化:
在本节中,我们分析了没有函数约束的多阶段控制代价最小化问题。 对于这个问题,我们在一般情况下提出了易于使用的最优性条件,这些条件被证明是必要的和充分的。 利用我们的条件,最优轨迹直接在时间和空间的线性复杂度中构建,无需显式或隐式评估代价函数。 基于这些条件,设计了一种新的轨迹类以及线性复杂度的时空变形,以满足各种轨迹规划场景中的用户定义目标。
4.1 无约束控制代价最小化
当约束 F 存在时,调整航路点 [28] 或控制点 [33] 有助于确保安全。 当约束 存在时,调整时间分配也有助于实施物理限制 [38]。 因此,空间和时间参数对于灵活的轨迹表示都是至关重要的。 一个自然的问题是根据这些参数生成平滑的轨迹。 我们解决线性二次最小时间 (Linear Quadratic Minimum Time) 问题,以根据时空参数生成轨迹。 尽管 LQMT 问题有广泛的研究和应用,但文献 [39]-[41] 中只考虑了单阶段问题。 我们研究了多段轨迹的中间点和时间向量预先固定的多阶段问题。 考虑没有 F 和 的 M阶段stage 控制代价最小化问题表示如下:
时间间隔 [![]() ,
, ![]() ] 通过 M+1 个固定时间戳分为 M 个阶段,具有恒定的边界条件
] 通过 M+1 个固定时间戳分为 M 个阶段,具有恒定的边界条件![]() ,
, ![]() ∈
∈ ![]() 。 中间条件
。 中间条件![]() ∈
∈ ![]() 且
且![]() 对于
对于![]() ,其中 di 是固定在 ti 处的导数。 例如,如果 z(t) 只需要通过
,其中 di 是固定在 ti 处的导数。 例如,如果 z(t) 只需要通过 ![]() 时刻的给定位置,则
时刻的给定位置,则 ![]() = 1,因为
= 1,因为![]() 包含 0 阶导数而没有其他内容。
包含 0 阶导数而没有其他内容。
现有的工作侧重于(18)的特殊情况的必要条件。 在空中机器人领域,QP 公式 [11] 和闭式解 [28] 隐式或显式优化未知节点导数,将参数化作为先验。 这种额外的计算实际上降低了它们的效率。 在控制领域,![]() = 1的特殊情况也在 [42] 和 [43] 中通过可控性 Gramian (controllability Gramian)进行了研究。 结果适用于可能具有非多项式解的一般线性系统,而考虑到计算方面则不太直观。 如果需要对时空参数进行进一步的参数优化,这些必要条件可能会导致轨迹表示和灵敏度的潜在退化。
= 1的特殊情况也在 [42] 和 [43] 中通过可控性 Gramian (controllability Gramian)进行了研究。 结果适用于可能具有非多项式解的一般线性系统,而考虑到计算方面则不太直观。 如果需要对时空参数进行进一步的参数优化,这些必要条件可能会导致轨迹表示和灵敏度的潜在退化。
4.2 最优性条件
我们为带有所有可能的参数的![]() 的式(18) 提出了必要且充分的最优性条件。 因此,可以直接从时空参数构建最佳轨迹。 此外,始终保证最优轨迹的存在性和唯一性。
的式(18) 提出了必要且充分的最优性条件。 因此,可以直接从时空参数构建最佳轨迹。 此外,始终保证最优轨迹的存在性和唯一性。
我们将 (18) 转换为 Mayer 形式 [23],其中由![]() 增强的新状态
增强的新状态![]() 定义为
定义为
我们设计了一个M阶段的增强系统运行过程,其中第i段是![]() 。值得注意的是,状态切换发生在这个运行过程中。严格地说,状态切换只在每个阶段开始时在
。值得注意的是,状态切换发生在这个运行过程中。严格地说,状态切换只在每个阶段开始时在![]() 上发生。定义
上发生。定义![]() 第 i 阶段的增强状态轨迹,由
第 i 阶段的增强状态轨迹,由 ![]() 和
和![]() 两部分组成。在每个时间戳
两部分组成。在每个时间戳![]() ,状态从 y[i] 转移到 y[i+1],并且部分
,状态从 y[i] 转移到 y[i+1],并且部分![]() 被重置为:
被重置为:
从而将部分状态从![]() 切换到 0。
切换到 0。![]() 部分在阶段之间保持连续,这意味着
部分在阶段之间保持连续,这意味着
(18c)和(18d)中的条件仍然满足,即
在这个过程中,式(18) 中的成本函数被转换为用于增强系统的每个阶段的terminal成本的总和,即,![\sum ^M_{i=1}\widetilde{y}_{[i]}(t_i)](http://img.e-com-net.com/image/info8/0370759116044eeea2a3ed2f49302888.gif) 。因此,增强系统和原始系统的最佳轨迹在中
。因此,增强系统和原始系统的最佳轨迹在中![]() 相同。
相同。
我们利用混合最大值原理 [44] 来推导最优解的必要条件。
定理1:混合极大值定理
让![]() 均为实数,且
均为实数,且![]() .对于任何绝对连续函数
.对于任何绝对连续函数![]() 的集合
的集合![]() , 定义一个向量
, 定义一个向量
![]()
在时间区间![]() 考虑问题:
考虑问题:
通过![]() 定义式(27)的优化过程。然后,存在一个集合
定义式(27)的优化过程。然后,存在一个集合![]() ,其中
,其中![]() 是Lipschitz连续。它产生了M个庞特里亚金函数。
是Lipschitz连续。它产生了M个庞特里亚金函数。
![]()
接下来的条件对所有k从1到M都满足:
(1):非平凡条件:![]()
(2):伴随方程![]()
(3):截断条件:![]()
证明:该证明可以直接改编自 Dmitruk 和 Kaganovich [44] 的定理 4。这里我们只考虑每个系统![]() 是时不变的,并且所有的间隔 Δk 都是固定的。此外,没有在
是时不变的,并且所有的间隔 Δk 都是固定的。此外,没有在![]() 上指定不等式约束。
上指定不等式约束。
根据定理1,协态![]() 在第i段状态中被定义为:
在第i段状态中被定义为:
![]()
其中![]() 。
。![]() 是
是![]() 中的第j段映射。式(20)的第i段庞特里亚金函数是:
中的第j段映射。式(20)的第i段庞特里亚金函数是:
![]()
通过应用![]() 的伴随方程(30),我们得到
的伴随方程(30),我们得到![]() ,这意味着
,这意味着![]() 是
是![]() 中的常数、 因此,
中的常数、 因此,![]() 始终是
始终是![]() 的二次函数:
的二次函数:
可以扩展为:
显然![]() 是
是![]() 阶多项式。
阶多项式。
根据最大化条件,在![]() 中
中![]() 的上边界总是0。
的上边界总是0。![]() 的正定性意味着
的正定性意味着![]() 。如果
。如果![]() ,然后式(35)变成
,然后式(35)变成![]() 的线性函数。零上边界意味着在
的线性函数。零上边界意味着在![]() 中
中![]() 。作为式(36)的结果,
。作为式(36)的结果,![]() 对所有在
对所有在![]() 的区间的t都成立。在这种情况下,发生了不能同时满足非奇异性条件(29)和横向性条件(31)的矛盾。 因此,
的区间的t都成立。在这种情况下,发生了不能同时满足非奇异性条件(29)和横向性条件(31)的矛盾。 因此,![]() 始终在整个️i中保持不变。 最优控制
始终在整个️i中保持不变。 最优控制![]() 可由下式获得:
可由下式获得:
![]()
然后,![]() 由s阶积分器
由s阶积分器![]() 推导出,是2s-1阶多项式。
推导出,是2s-1阶多项式。
为了进一步探索解的结构,我们利用增广系统的代价以及(23)、(24)和(25)中的所有约束条件来生成拉格朗日函数。 我们有
其中![]() 都是相应约束的常数系数。
都是相应约束的常数系数。![]() 给出了协态
给出了协态![]() 的边界值。
的边界值。
最后,通过替换式(36),(41),(43)到(39)中,我们得到了两个连续阶段的最优控制满足:
我们最终知道问题(18)的最优控制实际上是在时间戳![]() 处
处![]() 次连续可微。 因此,由m个2s-1次多项式组成的最优状态轨迹在ti处确实是
次连续可微。 因此,由m个2s-1次多项式组成的最优状态轨迹在ti处确实是![]() 次连续可微的。
次连续可微的。
现在我们将由(39)和(44)两个定理导出的条件归纳为式(18)的最优性的充要条件。
定理2:最优性条件
一条轨迹,由![]() 定义,是问题(18)的最优解,当且仅当以下条件被满足:
定义,是问题(18)的最优解,当且仅当以下条件被满足:
因此,对于这些条件,存在唯一的轨迹。
证明:从定理1直接得出的 (33) 到 (44) 的分析中,必要性的证明是显而易见的。充分性的证明如下所示 :
( a) 对于任何di序列,第一个和第四个条件始终确定维度为 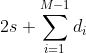 的线性样条空间;
的线性样条空间;
(b) 第二个和第三个条件显示为在样条空间的基础上形成一个平方系数矩阵;
(c) 矩阵被证明是非奇异的,因为对每个i来说![]() ,这意味着解的存在和唯一性;
,这意味着解的存在和唯一性;
(d) 必要条件的存在和唯一性产生了它们的充分性。充分性的证明细节在附录A中详述。
为了进一步解释最优性条件,我们以多阶段jerk最小化为例。在本例中,位置、速度和加速度是jerk控制系统的状态(s=3)。有一些中间点(![]() ),轨迹应该在特定的时间戳通过。状态的连续性只要求最小jerk轨迹的加速度的连续性,而最优轨迹的jerk和snap也处处连续。因此,如果我们强制所有这些连续性条件,那么定理2保证只存在一条轨迹,这正是最优轨迹。
),轨迹应该在特定的时间戳通过。状态的连续性只要求最小jerk轨迹的加速度的连续性,而最优轨迹的jerk和snap也处处连续。因此,如果我们强制所有这些连续性条件,那么定理2保证只存在一条轨迹,这正是最优轨迹。
4.3 无代价函数最小化
定理2提供了构造唯一最优轨迹的直接方法。计算在时间和空间上具有线性复杂性。它甚至不需要对成本函数或其梯度进行显式或隐式计算。
其中![]() 是基函数,
是基函数,![]() 是系数矩阵。为简单起见,我们使用相对于
是系数矩阵。为简单起见,我们使用相对于![]() = 0的时间线。轨迹由系数矩阵描述
= 0的时间线。轨迹由系数矩阵描述![]() 和一个时间向量定义为
和一个时间向量定义为![]() :
:
其中![]() 代表第i段的时间间隔。然后我们有时间戳
代表第i段的时间间隔。然后我们有时间戳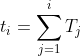 和总时间间隔
和总时间间隔![]() 。第M段轨迹
。第M段轨迹![]() 被定义为:
被定义为:
![]()
为了计算式 (18) 的唯一解,我们直接在系数矩阵 c 上强制执行最优条件。分别定义![]() 边界处的指定导数和中间时间戳
边界处的指定导数和中间时间戳![]() 。
。![]() 的每一列都与一个维度相关。然后,在
的每一列都与一个维度相关。然后,在![]() 时刻条件由
时刻条件由![]() :
:
特别地,定义![]() :
:
![]()
线性系统的最优系数矩阵是:
定理 2 中的唯一性必须确保 M 对于任何时间向量![]() 的非奇异性。因此,唯一解
的非奇异性。因此,唯一解![]() 可以通过具有带状矩阵 M 的线性方程组 (53) 获得,即带状系统。对于非奇异带状系统,其带状 PLU 分解始终存在 [45],可用于计算具有 O(M) 时间和空间复杂度的解 [46]。因此,在不需要代价函数的情况下,通过直接应用我们的最优条件,以最低复杂度获得问题 (18) 的唯一解。
可以通过具有带状矩阵 M 的线性方程组 (53) 获得,即带状系统。对于非奇异带状系统,其带状 PLU 分解始终存在 [45],可用于计算具有 O(M) 时间和空间复杂度的解 [46]。因此,在不需要代价函数的情况下,通过直接应用我们的最优条件,以最低复杂度获得问题 (18) 的唯一解。
4.4 带时空变形的MINCO轨迹
对于多旋翼飞行器,除了可行性之外,通常还有特定任务的要求,例如主动 SLAM [47] 中的感知质量或航空摄像中的遮挡率 [48]。这些用户定义的需求主要需要灵活和自适应地变形轨迹的空间和时间分布。因此,我们选择中间点和时间向量作为(18)中的两个重要参数。幸运的是,解的存在性和唯一性保证了它们的灵敏度平滑性。然后设计一个迭代程序,以每次迭代的最低计算复杂度进行时空变形
我们用![]() 表示中间点,其中
表示中间点,其中![]() 是ti时刻指定的0阶导数。用
是ti时刻指定的0阶导数。用![]() 表示
表示![]() 的时间向量。对于任何一对
的时间向量。对于任何一对![]() 和
和![]() ,定理2自然确定了属于一类控制代价最小化器的轨迹,称为MINCO
,定理2自然确定了属于一类控制代价最小化器的轨迹,称为MINCO
为简洁起见,此处省略了维度 m、系统阶数、初始条件和终止条件。直观地说,![]() 中的所有轨迹都仅由
中的所有轨迹都仅由![]() 和
和![]() 紧凑地参数化。评估
紧凑地参数化。评估 ![]() 中的元素直接遵循我们的线性复杂度公式。
中的元素直接遵循我们的线性复杂度公式。
我们将轨迹上的任何用户定义的目标(或约束)表示为![]() 函数
函数![]() ,
,![]() 上的目标值可被计算为:
上的目标值可被计算为:
![]()
为了完成![]() 的变形,高级优化器需要函数
的变形,高级优化器需要函数![]() 及其梯度
及其梯度![]() 和
和 ![]() 来优化目标。显然,评估W与评估
来优化目标。显然,评估W与评估![]() 中的任何轨迹具有相同的复杂性。关键过程是计算梯度。现在,我们给出了一个线性复杂度方案,以从给定的
中的任何轨迹具有相同的复杂性。关键过程是计算梯度。现在,我们给出了一个线性复杂度方案,以从给定的![]() 和
和 ![]() 中计算
中计算![]() 和
和 ![]() 。我们首先将线性方程组 (53) 重写为
。我们首先将线性方程组 (53) 重写为
为了不造成歧义,暂时为简单起见我们省略参数![]() 。任何为
。任何为![]() 的符号被解释
的符号被解释![]() 。定义
。定义![]() 为
为![]() 的第j个元素。
的第j个元素。
至于对![]() 求梯度,我们首先对式 (57)的两边求梯度,给出下式:
求梯度,我们首先对式 (57)的两边求梯度,给出下式:
其中 Tr (·) 是迹。 式(55) 中 b(q) 的定义意味着![]() 在其 (2i - 1)s + 1 行和 j 列只有一个非零条目 1。因此,堆叠所有结果标量给出:
在其 (2i - 1)s + 1 行和 j 列只有一个非零条目 1。因此,堆叠所有结果标量给出:
![]()
其中![]() 是
是![]() 的第j列。现在我们已经在计算
的第j列。现在我们已经在计算![]() 时对
时对![]() 进行了带状PLU因式分解。我们可以重复使用因式分解来避免对
进行了带状PLU因式分解。我们可以重复使用因式分解来避免对![]() 求逆。定义矩阵
求逆。定义矩阵![]() 为:
为:
![]()
我们只需要计算一次![]() 就可以得到
就可以得到![]() 中的所有
中的所有![]() 。表示
。表示![]() 的因式分解为
的因式分解为![]() 。具体地说,
。具体地说,![]() 是一个上带宽为零且对角线项均为1的带状矩阵。,由于
是一个上带宽为零且对角线项均为1的带状矩阵。,由于![]() 的非奇异性,
的非奇异性, ![]() 是一个下半部为0的带状矩阵,它具有非零对角线项。旋转矩阵P只是改变操作数的行顺序,满足
是一个下半部为0的带状矩阵,它具有非零对角线项。旋转矩阵P只是改变操作数的行顺序,满足![]() 。因此,转置也具有带状LUP因式分解[45]。具体而言,
。因此,转置也具有带状LUP因式分解[45]。具体而言,![]() ,其中
,其中
![]()
其中仅对 对角矩阵和 Hadamard 乘积进行逆运算。 然后,![]() 也可以通过这种分解以线性复杂度计算。 为方便起见,我们将
也可以通过这种分解以线性复杂度计算。 为方便起见,我们将 ![]() 划分为
划分为
对所有![]() ,
,![]() 之后,
之后,![]() 对
对![]() 的导数被确定为:
的导数被确定为:
其中![]() 是
是![]() 的第一列。此操作取出
的第一列。此操作取出 ![]() 中M− 1的特定列。两侧同时对
中M− 1的特定列。两侧同时对![]() 求导:
求导:
然后我们得到对![]() 求的梯度:
求的梯度:
![]()
其中,可以从 (49) 中解析得出。计算 (68) 对于每![]() ,就会得到
,就会得到![]() 。
。
最后,我们完成了![]() 和
和![]() 的计算。从式 (64) 和 式(68) 都可以验证,梯度传播也是在O(M) 复杂度下完成的。至于
的计算。从式 (64) 和 式(68) 都可以验证,梯度传播也是在O(M) 复杂度下完成的。至于![]() ,我们对它的具体形式不做任何假设。实际上,如果
,我们对它的具体形式不做任何假设。实际上,如果![]() 为
为![]() ,则甚至不需要
,则甚至不需要![]() 的平滑度。换句话说,线性复杂度梯度传播既具有效率又具有灵活性。通过将其合并到常见的优化器中,我们可以为广泛的规划目标完成
的平滑度。换句话说,线性复杂度梯度传播既具有效率又具有灵活性。通过将其合并到常见的优化器中,我们可以为广泛的规划目标完成![]() 的时空变形,同时保持轨迹的局部平滑度。
的时空变形,同时保持轨迹的局部平滑度。
5.几何约束飞行轨迹优化
在本节中,我们为飞行轨迹优化提供了一个统一的框架,具有不同的时间正则化 ρ(T)、空间约束![]() 和连续时间约束 。这个框架确实将原始问题放宽为
和连续时间约束 。这个框架确实将原始问题放宽为![]() 。 利用时空变形来满足各种可行性要求。 轻量级方案专门设计用于消除几何约束,使轨迹可以自由变形。 对于连续时间约束,提出了时间积分惩罚函数来确保可行性而不牺牲可扩展性。 最后,我们的框架将约束轨迹优化转换为可以可靠解决的稀疏无约束轨迹优化。
。 利用时空变形来满足各种可行性要求。 轻量级方案专门设计用于消除几何约束,使轨迹可以自由变形。 对于连续时间约束,提出了时间积分惩罚函数来确保可行性而不牺牲可扩展性。 最后,我们的框架将约束轨迹优化转换为可以可靠解决的稀疏无约束轨迹优化。
5.1 时间约束消除
变形MINCO需要标准的优化器,这些优化器通常是为欧几里德空间设计的。 然而,轨迹定义和代价泛函(11)都将T的域限制在简单流形上,在优化过程中需要在其上频繁地缩回。 我们给出了T的显式微分同胚,使得代理变量在欧几里德空间中。 因此,可以方便地应用常用的高效优化器。
对于多项式样条,(11)中的控制代价是c和T的函数,用![]() 表示。
表示。 ![]() 、
、![]() 和
和![]() 的解析表达式可在文献[28]中得到。 既然
的解析表达式可在文献[28]中得到。 既然![]() MINCO是系数由
MINCO是系数由![]() 决定的多项式样条,(11)的代价泛函可以写成
决定的多项式样条,(11)的代价泛函可以写成
![]()
其中![]() 定义为
定义为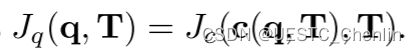 。显然地,能从任何提供的
。显然地,能从任何提供的![]() 在
在![]() 时间复杂度内计算出
时间复杂度内计算出![]() ,如
,如![]() 的变形所示。
的变形所示。
通过 ∂J/∂T 优化 T 是很自然的。然而,![]() 在
在![]() 上有其定义。当任何 Ti 接近零并且 q 中没有连续重复点出现时,它变得无界。此外,(13)中定义的
上有其定义。当任何 Ti 接近零并且 q 中没有连续重复点出现时,它变得无界。此外,(13)中定义的![]() 进一步将 J 的定义域限制为
进一步将 J 的定义域限制为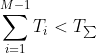 ,如图 3 所示。
,如图 3 所示。
图3:左图:总时间固定为![]() 的 M 段轨迹上的 J 的定义域上。该域确实是
的 M 段轨迹上的 J 的定义域上。该域确实是![]() 中 (M-1)-单纯形的相对内部。右图:ln J 的轮廓,M = 3。函数在
中 (M-1)-单纯形的相对内部。右图:ln J 的轮廓,M = 3。函数在![]() 时趋于无穷大。时间向量接近开放域的边界
时趋于无穷大。时间向量接近开放域的边界
我们使用微分同胚消除![]() 和
和 ![]() 的约束。考虑 (13) 中
的约束。考虑 (13) 中![]() 的定义域,
的定义域,
很明显,对于非平凡的![]() ,
,![]() 是有限的当且仅当
是有限的当且仅当![]() ,即
,即 ![]() 的相对内部。
的相对内部。
推论1:![]() 由(70)式定义,
由(70)式定义,
![]()
通过利用显式微分同胚(71),我们通过![]() 直接最小化
直接最小化![]() 上的代价函数
上的代价函数![]() ,因为默认情况下满足定义域约束。
,因为默认情况下满足定义域约束。
优化τ需要梯度传播。我们划分![]() ,其中
,其中![]() 和
和![]() 。 对式(71)中的层进行微分得到J关于
。 对式(71)中的层进行微分得到J关于![]() 的梯度,
的梯度,
其中![]() 是入口指数映射,
是入口指数映射,![]() 是全一向量。如果指定了初始值
是全一向量。如果指定了初始值![]() ,则可以通过给出的
,则可以通过给出的![]()
![]() 的微分同胚逆映射计算相应的
的微分同胚逆映射计算相应的![]() 。对于(12)中的
。对于(12)中的![]() ,只需要确保
,只需要确保![]() 。使用
。使用![]() 作为
作为![]() 和
和![]() 之间的微分同胚就足够了。
之间的微分同胚就足够了。
对于 ![]() 或
或 ![]() ,我们用
,我们用![]() 表示微分同胚。可以直接对
表示微分同胚。可以直接对![]() 进行无约束优化以最小化
进行无约束优化以最小化![]() 。尽管
。尽管![]() 不保持凸性,但原始成本
不保持凸性,但原始成本![]() 已经是非凸的,如 (57) 中给出的。因此,唯一的问题是
已经是非凸的,如 (57) 中给出的。因此,唯一的问题是![]() 是在
是在![]() 的空间中带来新的局部最小值还是在T的空间中消除局部最小值。
的空间中带来新的局部最小值还是在T的空间中消除局部最小值。
推论2:定义![]() 任何
任何![]() 函数带有凸开集定义域
函数带有凸开集定义域![]() ,给定任意
,给定任意![]() 微分同胚
微分同胚![]() ,定义
,定义![]() ,
,![]() ,其中
,其中![]() 。对任意
。对任意![]() 满足
满足![]() 或者等价地
或者等价地![]() ,以下陈述总是满足:
,以下陈述总是满足:
证明:见附录B
推论 2 证实了![]() 保留了一阶/二阶必要最优性条件和二阶充分最优性条件 [49]。 它也适用于用从
保留了一阶/二阶必要最优性条件和二阶充分最优性条件 [49]。 它也适用于用从![]() 到
到 ![]() 的任何
的任何 ![]() 微分同胚替换本小节中的指数映射,以获得更好的数值条件。 在常用的最优性条件的意义上,我们的约束消除不会产生额外的虚假局部最小值或取消任何现有的最小值。
微分同胚替换本小节中的指数映射,以获得更好的数值条件。 在常用的最优性条件的意义上,我们的约束消除不会产生额外的虚假局部最小值或取消任何现有的最小值。
5.2 空间约束消除
我们通过将轨迹限制在可行区域![]() 中来加强运动安全性。 尽管
中来加强运动安全性。 尽管![]() 是非凸的,但它是顺序连接的凸基元的并集。 如果所有轨迹段都被分配到这些基元中,则每条轨迹段的安全约束都是凸的,因此可以方便地用进行编码。由于MINCO的特性,每个基元的遍历时间可以直接优化。 因此,我们在优化之前固定了每条轨迹段的分配,而不是在优化过程中求助于整数变量[33]。 因此,中间点应该被原语之间的重叠所包含,从而形成不等式。 对于不等式约束问题(ICPs),一般的方法都是通过附加参数来逼近约束。 然而,我们的目标是直接有效地应用约束。 因此,我们提出空间约束消除,利用它们的几何性质来精确地执行它们。
是非凸的,但它是顺序连接的凸基元的并集。 如果所有轨迹段都被分配到这些基元中,则每条轨迹段的安全约束都是凸的,因此可以方便地用进行编码。由于MINCO的特性,每个基元的遍历时间可以直接优化。 因此,我们在优化之前固定了每条轨迹段的分配,而不是在优化过程中求助于整数变量[33]。 因此,中间点应该被原语之间的重叠所包含,从而形成不等式。 对于不等式约束问题(ICPs),一般的方法都是通过附加参数来逼近约束。 然而,我们的目标是直接有效地应用约束。 因此,我们提出空间约束消除,利用它们的几何性质来精确地执行它们。
考虑约束![]() ,其中P是闭球。 它的维数满足
,其中P是闭球。 它的维数满足![]() ,因为
,因为![]() 中还存在一个低维约束。 如果P是一个以点
中还存在一个低维约束。 如果P是一个以点![]() 为中心,半径为
为中心,半径为![]() 的闭球
的闭球![]()
我们利用平滑的满射将![]() 映射到
映射到![]() ,使得对
,使得对![]() 的优化隐含地满足约束
的优化隐含地满足约束![]() 。如图4所示,图是逆立体投影和正投影的组合。
。如图4所示,图是逆立体投影和正投影的组合。
图4:逆赤平投影![]() 将欧几里得空间
将欧几里得空间![]() 映射到一个没有北极
映射到一个没有北极![]() 的球体(n+1)维空间上。 在(n+1)维空间中。 正交投影
的球体(n+1)维空间上。 在(n+1)维空间中。 正交投影![]() 将
将![]() 映射到n维球
映射到n维球![]() 上。 变量ζ在Rn中自由移动,而变换后的变量Q停留在Bn中。 当q为球约束时,ζ的优化变为无约束 。
上。 变量ζ在Rn中自由移动,而变换后的变量Q停留在Bn中。 当q为球约束时,ζ的优化变为无约束 。
首先,我们利用逆立体投影将![]() 映射到
映射到![]() ,其中
,其中![]() 是一个没有北极的单位球体,即
是一个没有北极的单位球体,即
![]()
这确实是对![]() 的平滑投影。
的平滑投影。![]() 中除中心外的每个点都与
中除中心外的每个点都与![]() 中的两个点配对。
中的两个点配对。![]() 、
、![]() 和一个线性变换的合成,是一个光滑的满射
和一个线性变换的合成,是一个光滑的满射
![]()
映射![]() 引入了一个新的坐标,用 ξ 表示,使得在
引入了一个新的坐标,用 ξ 表示,使得在![]() 上优化 ξ 始终满足
上优化 ξ 始终满足![]() 描述的关于
描述的关于![]() 的约束。对于第i个中间点
的约束。对于第i个中间点![]() ,用
,用![]() 表示相应的新坐标。因此,用 ξ 表示
表示相应的新坐标。因此,用 ξ 表示![]() 的新坐标。优化 ξ 需要梯度传播。用
的新坐标。优化 ξ 需要梯度传播。用![]() 表示在
表示在![]() 中的第i个条目
中的第i个条目![]() 。微分
。微分![]() 给出梯度如下:
给出梯度如下:
![]()
如果优化需要从初始猜测![]() 开始,则可以通过使用
开始,则可以通过使用![]() 的局部逆来完成对 ξ 的反向评估,由
的局部逆来完成对 ξ 的反向评估,由![]() 给出,在1 ≤ i < M阶段:
给出,在1 ≤ i < M阶段:![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第28张图片](http://img.e-com-net.com/image/info8/9712c169c0f449cdb9b813c473133746.jpg)
同样,我们分析了平滑反射![]() 对
对![]() 中约束局部最小值的影响。尽管
中约束局部最小值的影响。尽管![]() 缺乏微分同胚所拥有的一一对应关系,但其组成部分都是良好形式的。首先,
缺乏微分同胚所拥有的一一对应关系,但其组成部分都是良好形式的。首先,![]() 只取一个点的前n个条目。此操作至少保留了
只取一个点的前n个条目。此操作至少保留了![]() 或
或![]() 中局部最小值的一阶必要条件。其次,
中局部最小值的一阶必要条件。其次,![]() 是
是![]() 和
和![]() 之间的微分同胚,从而满足推论2。因此,我们还可以确认
之间的微分同胚,从而满足推论2。因此,我们还可以确认![]() 不会产生额外的杂散局部最小值或取消任何现有的最小值。如图5所示,将2-D球内的约束最小值转换为无约束最小值。
不会产生额外的杂散局部最小值或取消任何现有的最小值。如图5所示,将2-D球内的约束最小值转换为无约束最小值。
图5。 二维球内凸函数![]() 的约束最小q*。 用
的约束最小q*。 用![]() 变换后,结函数
变换后,结函数![]() 变为非凸函数,但不引入额外的局部极小值
变为非凸函数,但不引入额外的局部极小值![]() ,保持了满足
,保持了满足![]() 的局部极小值ζ。
的局部极小值ζ。
5.3 多面体空间约束消除
现在我们考虑消除多面体约束。具体而言,P是一个闭凸多面体![]() ,定义如下:
,定义如下:
![]()
根据 (15)其中![]() 。常见的优化算法使用
。常见的优化算法使用![]() 的 H 表示作为线性不等式约束。 在我们的框架中,我们利用它们的几何特性来消除这些约束,以便
的 H 表示作为线性不等式约束。 在我们的框架中,我们利用它们的几何特性来消除这些约束,以便![]() 可以自由变形。为了实现这一点,我们使用
可以自由变形。为了实现这一点,我们使用![]() 的V表示,其中任何
的V表示,其中任何![]() 具有(一般)重心坐标,即顶点的凸组合。为了获得顶点,我们将高效的凸包算法【51】应用于基于赛德尔算法【52】计算的内点的
具有(一般)重心坐标,即顶点的凸组合。为了获得顶点,我们将高效的凸包算法【51】应用于基于赛德尔算法【52】计算的内点的![]() 对偶。注意,在我们的例子中,这个过程产生的开销可以忽略不计(n≤ 4) 。
对偶。注意,在我们的例子中,这个过程产生的开销可以忽略不计(n≤ 4) 。
消除多面体约束的过程如图 6 所示。我们将![]() 的所有
的所有![]() 个顶点表示为
个顶点表示为![]() ,其中每个 i 的 vi ∈ Rn。 点 q ∈ PH 的重心坐标由这些顶点的权重组成。 为了获得更紧凑的形式,定义
,其中每个 i 的 vi ∈ Rn。 点 q ∈ PH 的重心坐标由这些顶点的权重组成。 为了获得更紧凑的形式,定义![]() 和
和![]() ,则位置可以计算为:
,则位置可以计算为:
![]()
其中 ![]() 是重心坐标中的最后一个
是重心坐标中的最后一个![]() 项。凸组合中的坐标集也可以写成:
项。凸组合中的坐标集也可以写成:
图 6. 凸多面体上的变换。具有![]() 个顶点的凸多面体
个顶点的凸多面体![]() 实际上是重心坐标中的标准
实际上是重心坐标中的标准![]() -单纯形。那么单纯形
-单纯形。那么单纯形![]() 是具有球形域的入口方形图
是具有球形域的入口方形图![]() 的图像,可以如图 4 所示消除。
的图像,可以如图 4 所示消除。
文献 [37] 的多面体理论的主要定理证实了 (82) 下![]() 和
和![]() 的等价性。通过简单地添加辅助变量并将线性映射应用于q,多面体被精确地转换为标准
的等价性。通过简单地添加辅助变量并将线性映射应用于q,多面体被精确地转换为标准![]() -单形。该过程不会在优化问题中产生额外的非线性,除非增加决策变量的维数。因此,我们只考虑q上的决策变量作为相应的w。
-单形。该过程不会在优化问题中产生额外的非线性,除非增加决策变量的维数。因此,我们只考虑q上的决策变量作为相应的w。
单纯形 (83) 可以通过非线性变换消除。我们首先使用在(53)式中提出的入口方图![]()
![]() 去消除非负性限制使用
去消除非负性限制使用![]() 。然后
。然后![]() 上的约束
上的约束![]() 转换为在
转换为在![]() 上闭单位球体中
上闭单位球体中![]() 。
。
因此,我们可以再次利用 (78) 中的平滑满射![]() 。 式(82)、
。 式(82)、![]() 和
和![]() 的组合产生一个平滑的满射
的组合产生一个平滑的满射![]() 从
从![]() 到
到![]() :
:
![]()
![]() 引入了一个新的坐标 ξ,其中任何
引入了一个新的坐标 ξ,其中任何![]() 确保
确保![]() 。
。![]() 的边界也是可以达到的。
的边界也是可以达到的。
类似地,ξ 是 q 的新坐标。优化 ξ 需要梯度传播。用![]() 表示
表示![]() 中的第 i 个梯度
中的第 i 个梯度![]() ,然后对
,然后对![]() 进行微分得到:
进行微分得到:
如果指定了初始猜测![]() ,则可以通过
,则可以通过![]() 的局部逆计算相应的 ξ。 可以使用 Warren [54] 等人的分析方法获得每个
的局部逆计算相应的 ξ。 可以使用 Warren [54] 等人的分析方法获得每个![]() 的重心坐标。 之后,
的重心坐标。 之后,![]() 和
和 ![]() 的解析局部逆得到我们想要的
的解析局部逆得到我们想要的![]() 。 另一种灵活的方法是直接最小化
。 另一种灵活的方法是直接最小化 ![]() 和给定
和给定![]() 之间的平方距离。 这两种方法的时间消耗都可以忽略不计,但结果令人鼓舞。
之间的平方距离。 这两种方法的时间消耗都可以忽略不计,但结果令人鼓舞。
![]() 中的map
中的map![]() 为优化提供了额外的非线性。幸运的是,通过
为优化提供了额外的非线性。幸运的是,通过![]() 进行变量转换是不等式到等式转换的特例[55]。具体而言,不等式约束是
进行变量转换是不等式到等式转换的特例[55]。具体而言,不等式约束是![]() 。 通过引入附加变量
。 通过引入附加变量![]() ,等效等式约束为
,等效等式约束为![]() ,产生
,产生![]() 。Bertsekas证明,这种类型的约束转换能够保持[55]第4.3节中规定的ICP的一阶/二阶必要条件和二阶充分条件。我们证实,
。Bertsekas证明,这种类型的约束转换能够保持[55]第4.3节中规定的ICP的一阶/二阶必要条件和二阶充分条件。我们证实,![]() 中的附加非线性实际上并不排除期望的最小值或产生不期望的最小值。
中的附加非线性实际上并不排除期望的最小值或产生不期望的最小值。
对于![]() 或
或![]() ,使用平滑满射
,使用平滑满射![]() 消除了对 q 的直接约束。我们可以对 ξ 进行无约束优化,以最小化
消除了对 q 的直接约束。我们可以对 ξ 进行无约束优化,以最小化![]() 。
。
5.4 时间曲线惩罚函数
在消除直接约束后,![]() 可以自由变形以满足连续时间约束 。但是,在整个轨迹上强制 涉及无限多的不等式,这些不等式无法通过约束优化来解决。它还需要时间离散化,这通常会产生大量决策变量。为了保持轨迹参数化的稀疏性,我们将约束评估的分辨率与决策变量的数量分离。受约束转移[56]的启发,我们通过约束违反积分将转换为有限约束。
可以自由变形以满足连续时间约束 。但是,在整个轨迹上强制 涉及无限多的不等式,这些不等式无法通过约束优化来解决。它还需要时间离散化,这通常会产生大量决策变量。为了保持轨迹参数化的稀疏性,我们将约束评估的分辨率与决策变量的数量分离。受约束转移[56]的启发,我们通过约束违反积分将转换为有限约束。
对于一条轨迹![]() ,我们定义:
,我们定义:
其中![]() 和
和![]() 是入口最大值和入口幂函数的组合。 具体来说,如果
是入口最大值和入口幂函数的组合。 具体来说,如果![]() ,则需要进行平滑处理。函数型约束等价于等式约束
,则需要进行平滑处理。函数型约束等价于等式约束![]() 。实际上,
。实际上,![]() 是轨迹参数的函数,我们将其用作惩罚项。 如果 k = 1,它会形成一个非平滑但精确的惩罚。 如果 k > 1,则形成可微的严格凸惩罚项。 因此,可以采用
是轨迹参数的函数,我们将其用作惩罚项。 如果 k = 1,它会形成一个非平滑但精确的惩罚。 如果 k > 1,则形成可微的严格凸惩罚项。 因此,可以采用![]() 或
或![]() 的平滑近似。 为简单起见,除非另有说明,否则我们将在下文中使用
的平滑近似。 为简单起见,除非另有说明,否则我们将在下文中使用![]() 。 选择惩罚函数方法有两个原因。 首先,(87)中的积分只能用数值计算,使约束近似必然发生。其次,惩罚方法对构造不平凡的可行初始猜测没有要求。
。 选择惩罚函数方法有两个原因。 首先,(87)中的积分只能用数值计算,使约束近似必然发生。其次,惩罚方法对构造不平凡的可行初始猜测没有要求。
我们将 p(t) 的时间积分惩罚函数定义为:
![]()
其中![]() 是权重向量。通常,
是权重向量。通常,![]() 应该包含较大的常数。如果没有违反约束,则
应该包含较大的常数。如果没有违反约束,则![]() 保持为零。否则,如果 p(t) 上的任何部分违反中的任何约束,惩罚函数
保持为零。否则,如果 p(t) 上的任何部分违反中的任何约束,惩罚函数![]() 会迅速增长。通过将
会迅速增长。通过将![]() 并入代价函数,可以在可接受的容差内强制执行连续时间约束。
并入代价函数,可以在可接受的容差内强制执行连续时间约束。
实际上,![]() 只能通过求积来计算。 为了进行求积,我们首先定义一个采样函数
只能通过求积来计算。 为了进行求积,我们首先定义一个采样函数![]() :
:![]()
其中![]() ∈ [0, 1] 是一个归一化的标记。 然后
∈ [0, 1] 是一个归一化的标记。 然后![]() 的求积,表示为 I :
的求积,表示为 I : ![]() ,计算为采样惩罚的加权和,
,计算为采样惩罚的加权和,
其中![]() 控制分辨率。我们选择梯形规则
控制分辨率。我们选择梯形规则![]() ,因为它在我们的实践中具有可靠的性能。直观地,
,因为它在我们的实践中具有可靠的性能。直观地,![]() 是
是![]() 的可微近似,其精度可通过
的可微近似,其精度可通过![]() 调节。最多可以并行计算时间戳的值和梯度,然后直接组合为一个。
调节。最多可以并行计算时间戳的值和梯度,然后直接组合为一个。
5.5 无约束非线性规划--轨迹优化
由于(11)中的和 F,最优轨迹参数化通常很难知道。与通过大量变量近似解的传统方法[23]不同,我们建议通过无约束 NLP 解决轻量级松弛优化,其中应用了![]() 的时空变形。 (11)的松弛定义为:
的时空变形。 (11)的松弛定义为:
其中,J是![]() 的时间正则化控制力(69),I是惩罚函数(90)的求积。请注意,任何特定于任务的需求,无论是目标还是约束,都可以组合在(91)中,而不会影响其结构。
的时间正则化控制力(69),I是惩罚函数(90)的求积。请注意,任何特定于任务的需求,无论是目标还是约束,都可以组合在(91)中,而不会影响其结构。
为了生成平坦多旋翼飞行器的轨迹,我们首先将其平面输出轨迹参数化为 ![]() 。在将固定数量的片段分配给每个
。在将固定数量的片段分配给每个![]() 之后,应用变量变换来消除所有直接约束。用户定义的
之后,应用变量变换来消除所有直接约束。用户定义的![]() 也通过 Ψx 和 Ψu 转换为
也通过 Ψx 和 Ψu 转换为![]() 。最后,我们得到代价函数(91)。显然,梯度传播是针对除 Ψx 和 Ψu 之外的所有层得出的。可以将自动微分 (AD) [57] 应用于 Ψx 和 Ψu,或者通过遵循反向模式 AD 分析得出梯度传播。效率与 Baur-Strassen Theorem [58] 确保的平坦映射相同。对于给定的平坦动态,只需要一劳永逸地进行微分。使用可用的梯度,然后通过 L-BFGS 算法 [59] 求解松弛式 (91)。
。最后,我们得到代价函数(91)。显然,梯度传播是针对除 Ψx 和 Ψu 之外的所有层得出的。可以将自动微分 (AD) [57] 应用于 Ψx 和 Ψu,或者通过遵循反向模式 AD 分析得出梯度传播。效率与 Baur-Strassen Theorem [58] 确保的平坦映射相同。对于给定的平坦动态,只需要一劳永逸地进行微分。使用可用的梯度,然后通过 L-BFGS 算法 [59] 求解松弛式 (91)。
6.应用:
6.1 大规模无约束控制代价最小化
我们针对问题 (18) 对几种现有方案进行了基准测试,包括 Mellinger 和 Kumar [11] 的 QP 公式,Bry 等人 [28]的闭式求解方案。 以及 Burke 等人[60]的线性复杂度方案。我们在 C++11 中实现了所有这些方案,没有任何显式的硬件加速。 Mellinger 的方案是使用 OSQP [61] 实现的。 Bry 的解决方案由密集求解器和稀疏求解器评估 [62]。 为了公平起见,这里重新实现了 Burke 的方案,这比原来的方案要快 [60]。 基准测试是在 Linux 下的 Intel Core i7-8700 CPU 上进行的。 性能如图 7 所示。
jerk s = 3 和 snap s = 4 都按照 (18) 中的定义最小化。 Mellinger 的方案 [11] 在中等规模问题 (![]() ) 上的表现仅优于 Bry 的封闭式解决方案 [28] 的密集评估。 Burke 的方案 [60] 得益于其线性复杂性,因此它可以解决大规模问题(
) 上的表现仅优于 Bry 的封闭式解决方案 [28] 的密集评估。 Burke 的方案 [60] 得益于其线性复杂性,因此它可以解决大规模问题(![]() )。 我们的方案在任何问题规模上都将计算速度提高了几个数量级,同时保持了 O(M) 复杂度。
)。 我们的方案在任何问题规模上都将计算速度提高了几个数量级,同时保持了 O(M) 复杂度。
总之,我们的最优性条件为直接构造问题(18)的解决方案提供了一种实用的方法,它具有简单性、效率、稳定性和可扩展性。 轨迹类 ![]() 可以作为我们优化框架的可靠子模块。
可以作为我们优化框架的可靠子模块。
图7:计算时间![]() 。在不同的段数M下。顶部和中间数字分别给出了jerk最小化 (s = 3) 和snap最小化 (s = 4) 的性能。底部的图显示了针对非常大规模问题的两个线性复杂度方案的效率。
。在不同的段数M下。顶部和中间数字分别给出了jerk最小化 (s = 3) 和snap最小化 (s = 4) 的性能。底部的图显示了针对非常大规模问题的两个线性复杂度方案的效率。
6.2 基于安全飞行走廊的轨迹生成
作为问题 (11) 的一个特例,3-D 安全飞行走廊 (SFC) 内的轨迹生成已在 [31]、[63] 和 [64] 等实际应用中得到广泛采用。 SFC 通常由轨迹规划框架的前端生成,作为相关配置空间的抽象,例如平行凸簇膨胀 (PCCI) [31]、线搜索的区域膨胀 (RILS) [38]、安全区域 RRT* 扩展 [64] 或半定规划迭代区域通货膨胀 (IRIS) [65]。我们假设在 (14) 和 (15) 中已经获得了多面体形或球形的 SFC。在 SFC 中优化动态可行轨迹通常被视为此类框架的后端。
如图8所示,我们考虑两种SFC。每个凸基元分配有K个轨迹段,因此![]() 。第i个轨迹段
。第i个轨迹段![]() 分配给
分配给![]() . 还确定了
. 还确定了![]() 的中间点分配。应用约束消除,自动满足
的中间点分配。应用约束消除,自动满足![]() 和
和![]() 上的直接约束,例如
上的直接约束,例如![]() 表示
表示![]() ,对
,对![]() 而言
而言![]() ,以及对所有i而言
,以及对所有i而言![]() 。约束
。约束![]() 规定如下,以确保安全和动态极限:
规定如下,以确保安全和动态极限:
其中![]() 和
和![]() 是动力学限制。然后,可以通过求解 (91) 中的无约束NLP来完成 中的轨迹生成。我们在图9中显示了随机生成的sfc的一些优化结果。处理多面体和球形sfc。
是动力学限制。然后,可以通过求解 (91) 中的无约束NLP来完成 中的轨迹生成。我们在图9中显示了随机生成的sfc的一些优化结果。处理多面体和球形sfc。
图8.在![]() 中不同类型的安全飞行走廊内的轨迹碎片分配。 每个几何图元分配有 K 段轨迹。 中间点 qi 分配给
中不同类型的安全飞行走廊内的轨迹碎片分配。 每个几何图元分配有 K 段轨迹。 中间点 qi 分配给 ![]() 。 对于球形走廊,如果将一个点分配给两个 n 维球的交点,则该点将进一步锚定到 (n - 1) 维圆盘。
。 对于球形走廊,如果将一个点分配给两个 n 维球的交点,则该点将进一步锚定到 (n - 1) 维圆盘。
图9:不同种类的 3-D SFC 内的优化轨迹。 速度曲线根据其大小进行着色。 所提出的方法在随机生成的 SFC 内生成平滑的轨迹。 即使 SFC 狭窄和扭曲,速度也会持续达到最大值。
为了进一步评估我们方法的性能,我们对多面体形 SFC 的几种现有方法进行了基准测试。 所有方法的技术细节如下所示:
(1)本文提出的*:Jerk 能量最小化是通过线性时间正则化或固定总时间进行的。 式 (92) 中的约束被强制执行。
(2)Patterson[24]:使用高斯伪谱方法解决了加加速度控制系统的 LQMT 问题。 每个轨迹阶段都被限制在一个多面体中。 动态限制是通过路径约束来实施的。
(3)Gao*[31]:通过jerk能量消耗和线性安全约束形成的QP优化几何曲线贝塞尔曲线的控制点。然后在 (92) 下通过 SOCP 为 TOPP 优化其时间分布。
(4)Deits*[30]:通过MISOCP优化弹道的冲动能量和间隔分配。通过SOS条件,精确实施弹道导数L1范数的安全约束和动态限制。每个轨迹段是一个3次多项式。
(5)Deits:除了以启发式方式分配间隔之外,详细信息与deits*相同。不存在整数变量。
(6)Tordesillas*:细节与 Deits*相同,只是安全性由贝塞尔曲线控制点的线性约束来保证。而是解决了 MIQP。总时间由精心设计的算法确定。
(7)Mellinger:在QP中优化了轨迹,该QP由加加的二次成本和采样点的线性安全约束形成。它的时间分配是用梯形速度分布生成的。(92) 中的动态限制由时间缩放 [38] 强制执行。
(8)Sun*:在双层框架中优化轨迹。低级QP与Tordesillas完全相同,除了使用6次多项式。其时间分配在上层优化中利用下层优化的分析灵敏度进行优化。
如果方法支持优化时间分配或间隔分配,则该方法为星号。对于L1范数或L2范数,动力学限制被视为相同。因此,来自本文提出的,Gao*,Mellinger和patterson*的方法的约束确实要严格得多,这些方法限制了导数的L2范数。对于总时间,deits*和sun*需要预先分配值,因此,我们使用梯形速度曲线设置它们的总时间。Patterson∗直接处理原始问题,利用全局搭配的指数收敛性 [24]。因此,我们把它的轨迹作为地面真值。
基准测试是在随机生成的环境中进行的,其中之一如图 11 所示。走廊的大小![]() 的范围从 2 到 64,其中每个尺寸生成 10 个 SFC。
的范围从 2 到 64,其中每个尺寸生成 10 个 SFC。 ![]() 的分面数范围为 8 到 30。我们设置 K = 1,kρ = 1024.0,
的分面数范围为 8 到 30。我们设置 K = 1,kρ = 1024.0,![]() = 5.0m/s,
= 5.0m/s,![]() = 7.0
= 7.0![]() ,
,![]() = 16,超时时间为 3 分钟,相对容差 为
= 16,超时时间为 3 分钟,相对容差 为![]() 。 假定静态边界条件。 至于程序,本文方法 和 Mellinger 中的方法都是用 C++11 实现的,具有用于顺序计算的单线程。 Patterson*直接采用通用求解器[24]。 Deits*和 Deits 都采用了原始 MATLAB one [30] 的 C++11 重新实现。 Gao*、Tordesillas*和 Sun*的方法取自它们的开源实现。 此外,Deit*、Deits 和 Tordesillas*使用商业求解器 Gurobi [66],并启用了 6 个线程进行并行计算。 Gao*和 Sun*都使用商业求解器 MOSEK [67]。
。 假定静态边界条件。 至于程序,本文方法 和 Mellinger 中的方法都是用 C++11 实现的,具有用于顺序计算的单线程。 Patterson*直接采用通用求解器[24]。 Deits*和 Deits 都采用了原始 MATLAB one [30] 的 C++11 重新实现。 Gao*、Tordesillas*和 Sun*的方法取自它们的开源实现。 此外,Deit*、Deits 和 Tordesillas*使用商业求解器 Gurobi [66],并启用了 6 个线程进行并行计算。 Gao*和 Sun*都使用商业求解器 MOSEK [67]。
计算效率如图10所示。显然,Deits*和tordesillas*必须优化整数变量,因此随着![]() 的增长具有近似指数的复杂度。尽管如此,tordesilas*通过使用比deits*更保守的但更容易的约束来实现小型
的增长具有近似指数的复杂度。尽管如此,tordesilas*通过使用比deits*更保守的但更容易的约束来实现小型![]() 的可接受性能。Deits和Mellinger的方法通过启发式地处理时间分配或间隔分配来实现令人满意的性能。Gao*和sun*的方法在可扩展性方面表现良好,而小型
的可接受性能。Deits和Mellinger的方法通过启发式地处理时间分配或间隔分配来实现令人满意的性能。Gao*和sun*的方法在可扩展性方面表现良好,而小型![]() 的开销不适合实时应用。Patterson*的方法适用于计算时间远不如解决方案质量重要的离线场景。本文提出的方法将速度提高了一个数量级以上,同时保留了时间分配的优化。
的开销不适合实时应用。Patterson*的方法适用于计算时间远不如解决方案质量重要的离线场景。本文提出的方法将速度提高了一个数量级以上,同时保留了时间分配的优化。
图10:计算效率比较。本文提出的方法优于其他方法一个数量级。Tordesillas和deits的方法遭受组合爆炸,但在小规模问题上比patterson快。不支持时间或间隔优化的方法会牺牲质量而消耗更少的计算时间。
轨迹的几何曲线文件中如图11所示。不优化时间和间隔配置的方法更容易偏离地面真值。Deits*和 Tordesillas*方法产生的轨迹偏离了很多相比地面真值。因为间隔的分辨率有限。图12中给出了成功率、相对控制力和飞行持续时间。基于区间分配的方法的成功率相对较低。 所有的控制代价都被本文方法标准化,为了公平起见,它的总时间是相应的固定的。 显然,启发式时间或间隔分配会导致相对较高的控制代价。 此外,本文所提方法的飞行持续时间最接近真实情况。
![]()
图11:在随机环境中由不同方法生成的轨迹的几何曲线。 本文提出的轨迹比所有其他专业轨迹更接近 Patterson的基本真值。
图12:成功率、相对控制代价和飞行持续时间的基准比较。 Deits和 Tordesillas方法的成功率相对较低,因为它们优化了涉及整数变量的区间分配。 Deits 和 Mellinger 的方法具有相对较大的控制工作量,因为不支持时间或间隔分配的优化。 请注意,某些方法需要预先分配的总飞行时间。
为了探索时间曲线,我们还测试了如图13所示的长距离飞行中的四种完整方法。来自Gao*的轨迹没有其他的那么激进。由于使用了3次多项式,因此来自tordesillas*的轨迹具有不连续的jerk。本文方法的结果与基本真值的质量几乎相同。从惩罚函数的有效性中获利,我们的方法还可以持续实现最大速度。
在仿真中,我们的方法在几何和时间曲线上实现了与基于搭配的方法 [24] 相当的轨迹质量,同时具有优于所有基准测试的计算速度。
图13:具有大权重时间正则化的轨迹曲线。考虑到导数范数的连续时间约束,只有本文方法和来自 Patterson 的方法会产生持续紧密的轨迹。
我们通过在地下车库中实现多旋翼飞行器的高速自主飞行来对我们的框架进行实验验证。 所有计算均由具有 Intel Core i7-8550U CPU 的板载计算机执行,如图 14 所示。我们利用 FAST-LIO2 [68] 进行高度稳健的基于 LiDAR 的定位。 多面体形安全飞行走廊由以下[31]生成。 我们的方法在第一条轨迹中仅用 0.29 秒就生成了 343.57m 的全局轨迹。 规划结果如图 1(c) 所示。 我们相信这个计算时间验证了我们框架的效率,即使对于长距离轨迹规划也是如此。 在本实验中,飞行速度达到12.0m/s,同时保证了其在障碍物中的安全性,并保持了较低的推重比。 我们进一步比较了![]() 上不同参数的规划结果。 事实证明,如果 kρ 很大,我们的方法总是可以压缩
上不同参数的规划结果。 事实证明,如果 kρ 很大,我们的方法总是可以压缩![]() 和
和![]() 的能力。 关于这个实验的更多细节在附加的多媒体材料中给出。
的能力。 关于这个实验的更多细节在附加的多媒体材料中给出。
图14:左:我们的自主多旋翼飞行器配备了机载计算机和激光雷达。右图:我们在车库进行高速飞行实验时的第一人称视角快照。
6.3 在商空间(Quotient Space)的SE(3)运动规划
在密集的障碍物环境中,狭窄的空间通常不存在安全运动,除非多旋翼飞行器敏捷地调整其姿态以避免碰撞。 因此,我们在我们的框架中考虑 SE(3) 运动规划。 在 SE(3) 中规划为具有结构![]() ×SO(3) 的流形的一个重要属性是刚体的可行位姿至少包含无量纲点的可行平移的必要条件。 子空间
×SO(3) 的流形的一个重要属性是刚体的可行位姿至少包含无量纲点的可行平移的必要条件。 子空间![]() 被称为商空间 [69]。 利用这种商空间分解[70],我们考虑基于平移轨迹的旋转安全性,而不是联合处理它们。因此,我们可以放宽对 (14) 的假设,使得
被称为商空间 [69]。 利用这种商空间分解[70],我们考虑基于平移轨迹的旋转安全性,而不是联合处理它们。因此,我们可以放宽对 (14) 的假设,使得![]() 只是商空间中的一个自由区域而不去考虑多旋翼的实际尺寸。
只是商空间中的一个自由区域而不去考虑多旋翼的实际尺寸。
我们考虑简化的四轴飞行器动力学,其配置由其平移 p 和旋转 R 定义:
![]()
其中![]() 是
是![]() 的第i列,
的第i列,![]() 为重力加速度,
为重力加速度,![]() 推力,ω 为角速度输入,
推力,ω 为角速度输入,![]() 为设备质量。hat映射
为设备质量。hat映射 ![]() 对于所有的
对于所有的![]() 由
由![]() 定义。此外,我们将对称多旋翼飞机的几何形状建模为其外部所有者John ellipsoid [37],
定义。此外,我们将对称多旋翼飞机的几何形状建模为其外部所有者John ellipsoid [37],
![]()
其中![]() 。
。![]() 分别是多旋翼的半径和长度。
分别是多旋翼的半径和长度。
可行的运动满足安全和动力学限制。 安全性是指![]() , ∀t ∈ [0, T],其中 T 是运动的总时间。 然而,这种安全约束确实难以执行。 我们进一步对
, ∀t ∈ [0, T],其中 T 是运动的总时间。 然而,这种安全约束确实难以执行。 我们进一步对![]() 做出假设,即所有
做出假设,即所有![]() 或其交点都能够包含至少一个多旋翼的椭球。 当
或其交点都能够包含至少一个多旋翼的椭球。 当![]() 增量生成时,可以合理地满足这个假设。 因此,我们可以通过以下方式确保安全:
增量生成时,可以合理地满足这个假设。 因此,我们可以通过以下方式确保安全:
动力学极限是指速度、推力和角速度应该有合理的大小,
给定商空间轨迹 ![]() ,p、v、R 和 ω 的状态控制轨迹都由动力学的平坦度映射 Ψx 和 Ψu 代数计算 (93)。 代数映射的具体形式在 [11] 中有详细说明,其中固定了简单四轴飞行器的角速度 [14],因此这里省略。 因此,也获得了整个 SE(3) 轨迹。 用 R(t) 表示它的旋转部分。 为了在
,p、v、R 和 ω 的状态控制轨迹都由动力学的平坦度映射 Ψx 和 Ψu 代数计算 (93)。 代数映射的具体形式在 [11] 中有详细说明,其中固定了简单四轴飞行器的角速度 [14],因此这里省略。 因此,也获得了整个 SE(3) 轨迹。 用 R(t) 表示它的旋转部分。 为了在![]() 中生成 p(t),我们遵循之前实验的方法,但这里有不同的约束。
中生成 p(t),我们遵循之前实验的方法,但这里有不同的约束。
第i个轨迹段![]() 被分配给 (17) 中定义的多面体
被分配给 (17) 中定义的多面体![]() ,其中
,其中![]() 。我们
。我们![]() 表示由
表示由![]() 和 (94) 中定义的相应
和 (94) 中定义的相应![]() 诱导的椭球。正如Wu等人 [71] 提出的,通过将设备椭球限制在多面体中来确保安全性也具有分析形式。具体来说,
诱导的椭球。正如Wu等人 [71] 提出的,通过将设备椭球限制在多面体中来确保安全性也具有分析形式。具体来说,
等价于:
其中 ![]() 是具有适当长度的全一向量,
是具有适当长度的全一向量,![]() 和
和![]() 分别是入口平方和平方根。 最后,我们为(93)中考虑的动力学获得了(8)中的状态控制约束
分别是入口平方和平方根。 最后,我们为(93)中考虑的动力学获得了(8)中的状态控制约束![]() 。 我们选择最小化 s = 3,因为它是 (93) 平坦度的最高导数阶,并且也有助于平滑角速率。
。 我们选择最小化 s = 3,因为它是 (93) 平坦度的最高导数阶,并且也有助于平滑角速率。
我们在仿真中验证了我们的框架,其中需要相对较大的四轴飞行器飞过宽度小得多的狭窄间隙,如图 15 所示。设置为![]() = 0.5m,
= 0.5m,![]() = 0.1m,
= 0.1m,![]() = 5.0
= 5.0![]() ,
,![]() ,
,![]() = 6.5m/s,
= 6.5m/s,![]() = 5.2rad/s。 直观地说,四轴飞行器每秒只能达到不超过 1 转 (rps),这使得它的敏捷性低于可以达到 5 rps 的小型四轴飞行器 [72]。 不同
= 5.2rad/s。 直观地说,四轴飞行器每秒只能达到不超过 1 转 (rps),这使得它的敏捷性低于可以达到 5 rps 的小型四轴飞行器 [72]。 不同 ![]() 的计算时间、所需的滚动角和 SE(3) 运动如表 I 和图 15(b)-15(f) 所示。
的计算时间、所需的滚动角和 SE(3) 运动如表 I 和图 15(b)-15(f) 所示。
图15:窄间隙的 SFC 布局、不同间隙宽度下的 SE(3) 轨迹以及不同运动的控制输入。随着间隙变窄,安全飞行需要更大的角速率和更高的推力。所提出的方法在不同设置下持续对这些控制输入实施限制,同时保留毫秒级计算时间。
随着窄缝变得更窄,所需的滚转角变大的和可行的空间变得越来越小的动力学限制。我们的方法仍能发现所有可行的运动。优越的计算速度使得在高频(至少100Hz)下求解SE(3)规划成为可能。约束函数如图15(g)所示。速度和推力始终满足动态限制。在![]() 的连续时间中
的连续时间中![]() 显示了我们的惩罚函数的有效性。
显示了我们的惩罚函数的有效性。
我们在一个真实的实验中评估了我们的规划器的性能,在这个实验中,一架四旋翼直升机穿过几个狭窄的窗口。图16给出了四旋翼机和窗口的尺寸。这架四翼直升机重794.2克。短边的安全裕度只有5.4cm,这意味着可行的运动空间非常小。设定值为![]() =20.0cm,
=20.0cm,![]() =4.6cm,
=4.6cm,![]() =4.0m/s,
=4.0m/s,![]() ,
,![]() ,
,![]() ,K=2。飞行空间限制为6.5×6.0×2.0
,K=2。飞行空间限制为6.5×6.0×2.0![]() 。窄窗和四翼直升机的所有姿态都由一个以100hz运行的动捕系统提供。对于自由体积中的多个窄窗口,从几何角度计算无障碍区域F。规划器在offboard计算机上运行,其中操作员可以任意选择目标位置。我们采用Faessler等人[14]的控制算法进行机载SE(3)轨迹跟踪。
。窄窗和四翼直升机的所有姿态都由一个以100hz运行的动捕系统提供。对于自由体积中的多个窄窗口,从几何角度计算无障碍区域F。规划器在offboard计算机上运行,其中操作员可以任意选择目标位置。我们采用Faessler等人[14]的控制算法进行机载SE(3)轨迹跟踪。
图16:无人机和狭窄窗户的尺寸
第一个场景包含滚转角度范围为![]() 的连续窗口. 四旋翼直升机必须飞越它们,并达到随机选择的目标,如图17(b)-17(e)所示。第二种场景是交互式场景,其中,如图17(a)所示,人工操作员随机持有一个用于实时规划的窄窗口。第三种情况需要四架直升机在多个窗口中持续来回飞行很长时间,如图1(b)和图1(d)所示。我们的规划器引导四旋翼直升机在20.0秒左右的时间内在窗口来回飞行,同时始终确保安全和物理限制。有关此实验的更多详细信息,请参阅随附的多媒体资料。
的连续窗口. 四旋翼直升机必须飞越它们,并达到随机选择的目标,如图17(b)-17(e)所示。第二种场景是交互式场景,其中,如图17(a)所示,人工操作员随机持有一个用于实时规划的窄窗口。第三种情况需要四架直升机在多个窗口中持续来回飞行很长时间,如图1(b)和图1(d)所示。我们的规划器引导四旋翼直升机在20.0秒左右的时间内在窗口来回飞行,同时始终确保安全和物理限制。有关此实验的更多详细信息,请参阅随附的多媒体资料。
在这个实验中,连续窗户之间的短距离,小的加减速空间,以及有限的设备机动性是我们的规划器必须面对的挑战。我们认为这些结果为其约束逼真度、运动质量、计算效率和鲁棒性提供了有力的证据。然而,我们观察到了基于优化的方法的局限性。例如,如果两个90度的窗口不对称地放置,多路飞行器必须依次通过它们。每个窗口只允许两个滚动角 ±![]() 。组合是4个局部最优机动,但只有一个是全局最优的。因此,其他三个是局部方法不可避免的浅局部极小值。
。组合是4个局部最优机动,但只有一个是全局最优的。因此,其他三个是局部方法不可避免的浅局部极小值。
图17:三个 SE(3) 规划方案的实验结果。图 17(a) 给出了交互式场景的快照。图 17(b)-17(c) 显示了通过连续窗口的真实飞行的两个快照。图 17(d)-17(e) 显示了由所提出的方法生成的相应 SE(3) 轨迹。
7.讨论和总结:
7.1 扩展
得益于灵活性和效率,我们的框架具有许多应用和算法扩展。 首先,从未对设备动力学的具体形式和环境![]() 做出任何假设。可以采用更精确的动力学,例如转子阻力 [14],通过实时高保真规划和控制来充分利用物理极限。
做出任何假设。可以采用更精确的动力学,例如转子阻力 [14],通过实时高保真规划和控制来充分利用物理极限。![]() 也可以支持移动障碍物的时间相关约束。 其次,我们的框架本质上是可并行化的,以进一步压缩其性能。
也可以支持移动障碍物的时间相关约束。 其次,我们的框架本质上是可并行化的,以进一步压缩其性能。![]() 上的计算要求操作在每个时间戳上都是独立的,因此并行化可以有效地加速我们的优化。 此外,可以将我们的方法扩展到其他平面输出空间与配置空间重叠的车辆类型。 一个例子是[28]中的固定翼飞机,其飞行主要受轨迹曲率的限制。 布赖等人 [28] 提出 Dubins-Polynomial 轨迹用于该限制,而曲率约束是
上的计算要求操作在每个时间戳上都是独立的,因此并行化可以有效地加速我们的优化。 此外,可以将我们的方法扩展到其他平面输出空间与配置空间重叠的车辆类型。 一个例子是[28]中的固定翼飞机,其飞行主要受轨迹曲率的限制。 布赖等人 [28] 提出 Dubins-Polynomial 轨迹用于该限制,而曲率约束是![]() 的特例,用于 MINCO。
的特例,用于 MINCO。
为了证明可扩展性,我们将我们的框架应用于一群多旋翼飞行器,以实现它们在未知环境中的自主导航。 技术报告 [73] 中给出了公式 (11) 和实际飞行的所有细节。
7.2 限制
与大多数基于优化的框架一样,我们的框架侧重于轨迹规划的局部解决方案,因此受到局部最小值的影响。 正如 [74]-[76] 中所提出的,这可以通过将基于采样或基于图搜索的策略交织到我们的框架中来缓解。 该框架的一个主要限制源于 MINCO 本身。 如果![]() 存在,最优解通常不能用多项式样条表示,更不用说 MINCO。 因此优化 MINCO 只是对原始问题的一种放松。 然而,我们的结果表明,MINCO 仍然可以代表与地面真值相当的高质量解决方案,但计算速度要快几个数量级。 惩罚函数也有限制。 为了实现零约束违规,需要一个无界的平滑因子或惩罚权重和一个无界的正交分辨率。 然而,对多旋翼导航来讲小的约束违反在经验上是可以接受的。因此,本文方法不需要初始可行的状态估计。
存在,最优解通常不能用多项式样条表示,更不用说 MINCO。 因此优化 MINCO 只是对原始问题的一种放松。 然而,我们的结果表明,MINCO 仍然可以代表与地面真值相当的高质量解决方案,但计算速度要快几个数量级。 惩罚函数也有限制。 为了实现零约束违规,需要一个无界的平滑因子或惩罚权重和一个无界的正交分辨率。 然而,对多旋翼导航来讲小的约束违反在经验上是可以接受的。因此,本文方法不需要初始可行的状态估计。
7.3 总结
在本文中,我们提出了一个灵活的多旋翼轨迹规划框架,该框架由几个核心特征提供支持,例如基于最优条件的 MINCO 轨迹、基于平滑映射的约束消除方案、基于约束转移的惩罚函数方法以及后向微分的平坦映射(来自平坦输出)。所有这些组件都享有源自低复杂性和较少初步假设的效率和通用性。我们针对多种多旋翼轨迹规划方法进行了广泛的基准测试,以显示超过数量级的加速和顶级解决方案质量。各种应用程序展示了我们框架的多功能性。我们还进一步讨论了几个未列出的应用程序或扩展作为未来的工作。
8 附录
A.定理2的充分性证明。
B.推论2的证明。
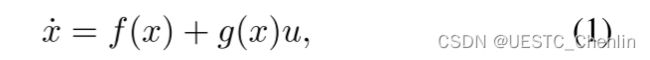
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第1张图片](http://img.e-com-net.com/image/info8/3c4ab65a602949dfbbadbc43493af8b8.jpg)

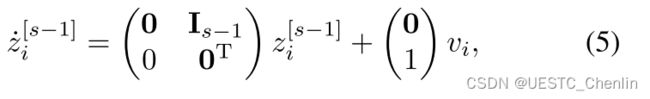
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第2张图片](http://img.e-com-net.com/image/info8/009ad223e4ac490d9c904a8e4626b0c4.jpg)
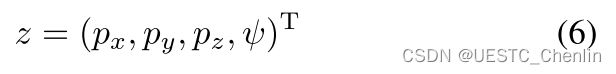
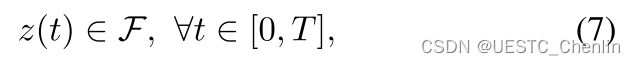
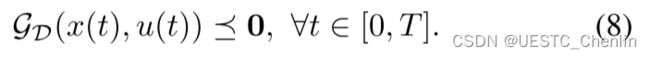
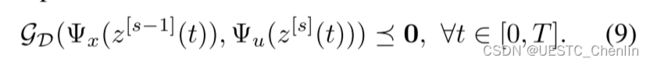
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第3张图片](http://img.e-com-net.com/image/info8/46089cafb4b746408437235e06216a47.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第4张图片](http://img.e-com-net.com/image/info8/a0f6ebf9c2d945ababefbaee7380ea9e.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第5张图片](http://img.e-com-net.com/image/info8/b914f1143cd644898c19d014cd8ac3b2.jpg)
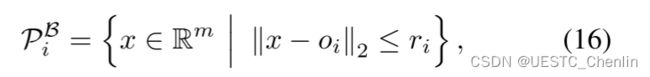
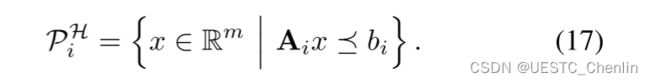
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第6张图片](http://img.e-com-net.com/image/info8/56c5a254bc03465d81836428ff6bd78c.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第7张图片](http://img.e-com-net.com/image/info8/a819b97929944b58af2684a97cdf9dc3.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第8张图片](http://img.e-com-net.com/image/info8/e6cc67bc0d0f4c6c90507bb2166e902e.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第9张图片](http://img.e-com-net.com/image/info8/4c4f11f97783449b979e745b04c87b35.jpg)
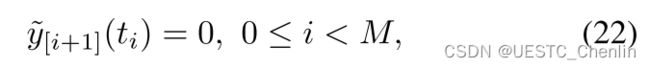
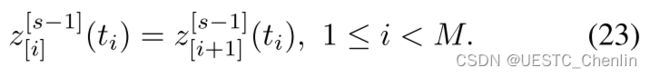
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第10张图片](http://img.e-com-net.com/image/info8/2997331b83d842f9992977fb93f90c91.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第11张图片](http://img.e-com-net.com/image/info8/72d277661537425c98ed858b6d4c6de5.jpg)

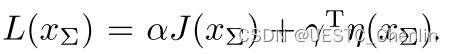
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第12张图片](http://img.e-com-net.com/image/info8/dcf82fcbad28447894f6b4ddaf17479b.jpg)
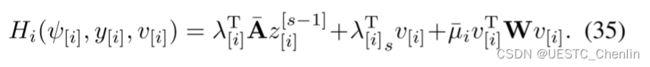

![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第13张图片](http://img.e-com-net.com/image/info8/b8a100dd139f4eb096bc77307113f754.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第14张图片](http://img.e-com-net.com/image/info8/38ac3345164543f8990b5c0e1043e8e7.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第15张图片](http://img.e-com-net.com/image/info8/2c14c988d65c4479893178a07d9b6ee8.jpg)
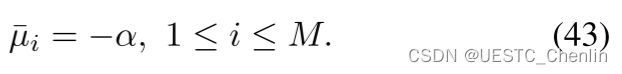
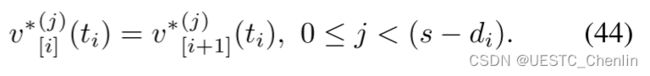
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第16张图片](http://img.e-com-net.com/image/info8/a19af9117e4b4b56a21b62ddfb054c72.jpg)
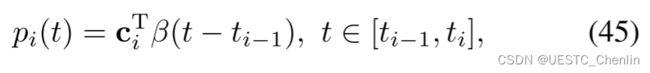
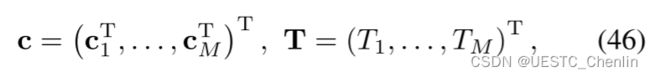
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第17张图片](http://img.e-com-net.com/image/info8/cdfca75839a64a64b05ff0a8ca0f7458.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第18张图片](http://img.e-com-net.com/image/info8/ae8bd04ab4c24c63ba2abb4349f86331.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第19张图片](http://img.e-com-net.com/image/info8/06ef4d4922524ab9931fa46fd1220e25.jpg)
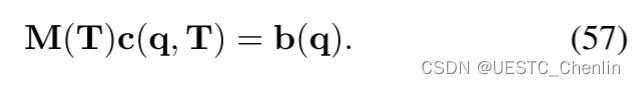
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第20张图片](http://img.e-com-net.com/image/info8/d9da29911ff14ff4bc75d4a78dcfade6.jpg)
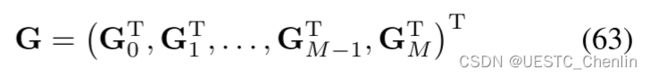
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第21张图片](http://img.e-com-net.com/image/info8/ebdfa54093e24d3a86be558bdc735a78.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第22张图片](http://img.e-com-net.com/image/info8/8176891c580b4c03ab3719ee5cc3b148.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第23张图片](http://img.e-com-net.com/image/info8/b6e18213567e45669cd47e19fcb301ba.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第24张图片](http://img.e-com-net.com/image/info8/63e07c29a60e464190321b460ec5e8a7.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第25张图片](http://img.e-com-net.com/image/info8/d1994ef671194fc1b55af808cf555519.jpg)
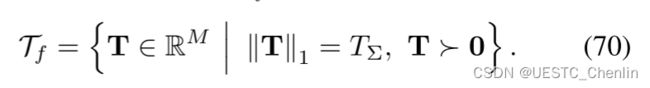
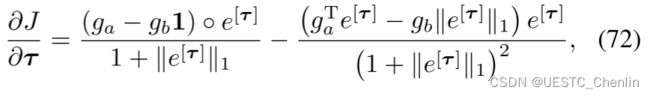
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第26张图片](http://img.e-com-net.com/image/info8/c5eb5a3fc0674cf5959f762cdaea26ee.jpg)
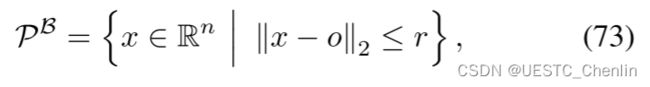
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第27张图片](http://img.e-com-net.com/image/info8/7585b1e492c847f68e6cfa2b732cd5ae.jpg)
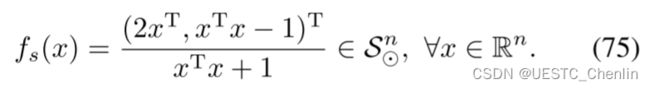
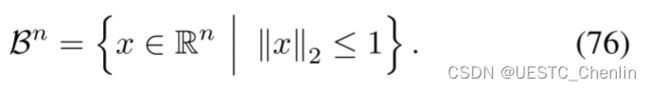
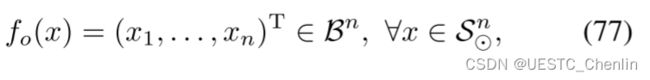
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第29张图片](http://img.e-com-net.com/image/info8/c5ede88743864d27a85cfabbef818e55.jpg)
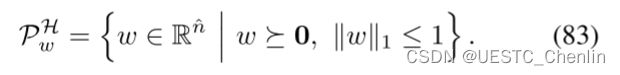
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第30张图片](http://img.e-com-net.com/image/info8/1a2a95bc538746319560d0e0a62e0074.jpg)
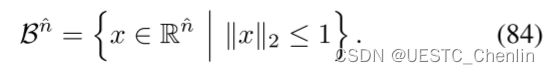
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第31张图片](http://img.e-com-net.com/image/info8/1c0a203046584f25b455a1d98aadb053.jpg)
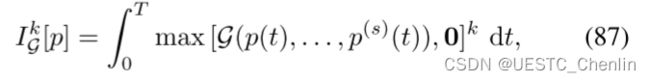
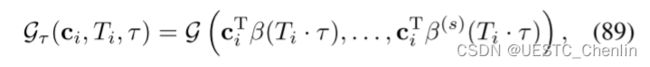
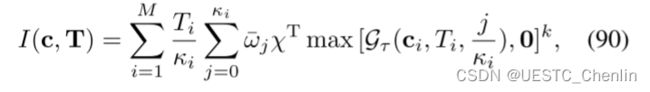
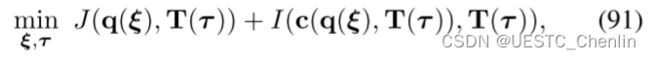
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第32张图片](http://img.e-com-net.com/image/info8/cdaa1005511b45f1b471ce3ab08f3258.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第33张图片](http://img.e-com-net.com/image/info8/dd87a4a0e93f40bfbf66d1fb696136b1.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第34张图片](http://img.e-com-net.com/image/info8/38f6e910ec644962bfd27b2dc3f56415.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第35张图片](http://img.e-com-net.com/image/info8/cba3df1c425647318ca6fdcdd9add118.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第36张图片](http://img.e-com-net.com/image/info8/c7c0c28efbcd44089eb8f0cfaf31042d.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第37张图片](http://img.e-com-net.com/image/info8/50f9825dbbcd4e46aef5e375bbaf16d2.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第38张图片](http://img.e-com-net.com/image/info8/2a4ac88f9f1d49d982f94f24374f2829.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第39张图片](http://img.e-com-net.com/image/info8/4eb1ee65d8024438bdd9056a066618a7.jpg)
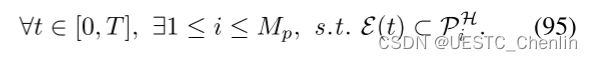
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第40张图片](http://img.e-com-net.com/image/info8/c45c43145ba14634ab86049b8ac4aa68.jpg)
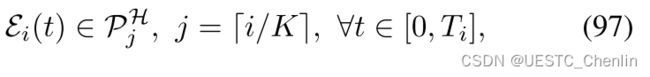
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第41张图片](http://img.e-com-net.com/image/info8/4b27a2d64f65487ab610199efbfc6370.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第42张图片](http://img.e-com-net.com/image/info8/dde79634da4848e38658fe4ae87121e9.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第43张图片](http://img.e-com-net.com/image/info8/3da09b1abb79409f813855f714f6d0dd.jpg)
![[论文笔记]Geometrically Constrained Trajectory Optimization for Multicopters_第44张图片](http://img.e-com-net.com/image/info8/8cda41ac65d74c59b4df48fb3c988e56.jpg)