主成分分析（principal component analysis, PCA）公式

主成分分析

摘要

主成分分析作为一种常见的数据降维（dimension reduction）的方法，在数据科学的许多领域（比如图像压缩，时间序列预测等）都有广泛的应用。本文将简要介绍主成分分析的概念及相关公式。

什么是主成分

要对一组数据进行主成分分析（principal component analysis, PCA），我们首先要理解什么是主成分。概括地说，主成分是一个向量，这个向量在较低维度上概括了原来的较高维度数据的分布。假设我们的原始数据（红色的点）如下图中红色的点所示。

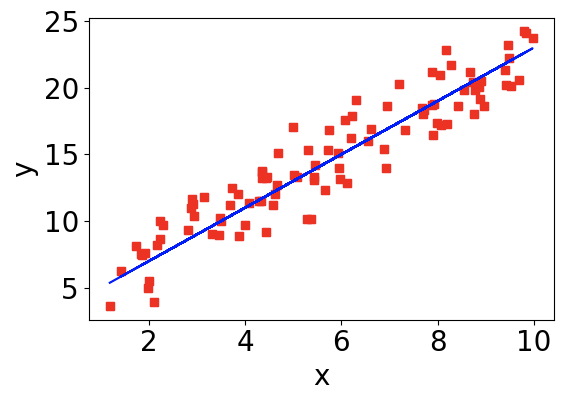
我们看到，每一个红色的点都有两个坐标，我们记为 $(x,y)$。但是我们发现红色点的分布可以用蓝色的直线来近似。如果对于每一个红色的点 $(x_i,y_i)$，我们由 $(x_i,y_i)$ 向蓝色的线做垂线（即做投影），那么我们将在蓝色的线上得到一个与$(x_i,y_i)$ 对应的点。如果我们在蓝色的线上规定一个原点，那么这个点在蓝色的线上对应的坐标就是一个实数，记为 $z_i$。于是，对于每一个红色的点$(x_i,y_i)$，我们有一个对应的点 $z_i$。这样，我们就把一个二维的数据转化为用一维数据来表示。这条蓝色的直线所代表的方向就是红色点集合的第一主成分。

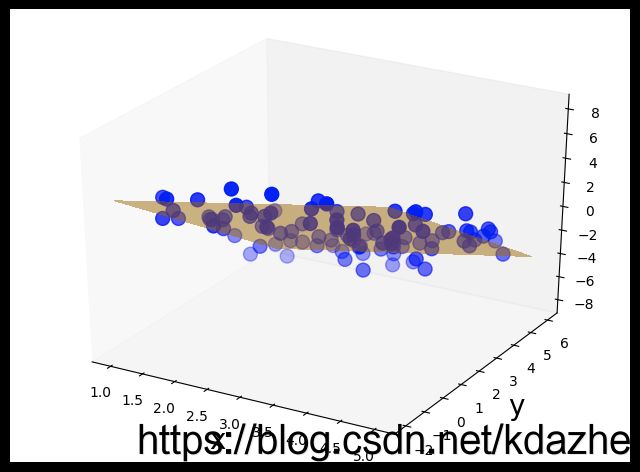
对于三维的数据，类似的，我们同样可以根据数据点的分布找到能代表数据的主成分方向，如图2所示。图中蓝色的点代表原始的三维数据，而橙色的平面表示原始数据第一主成分与第二主成分所构成的平面。那么，我们将原始的数据向这个平面投影，每个三维的数据点$(x_i,y_i,z_i)$ 就会映射成一个二维的点$(w_{1i},w_{2i})$。

通过上面两个例子，我们看到主成分分析可以帮助我们将原始的高维数据用低维的数据来表示，从而实现数据降维（dimension reduction）的目的。这在数据维度非常多的情况下，可以大大减少数据维度与存储空间。

对于二维和三维的情况，我们尚且能通过画图看出数据的大致分布。但是对于 $p$ 维 $(p\ge 3)$ 的数据，我们不能将数据绘制出来。这时候怎么办呢？这正是我们须要用主成分分析（principal component analysis, PCA）的地方。PCA 可以帮助我们将高维的数据转化成低维的表示。

当然，在这个过程中，我们只是用低维数据去近似表示原来的高维数据。也就是说，我们筛选出了原来高维数据中信息含量最大的那些维度。

求解 PCA 的公式

怎么去求PCA中的主成分方向（或是主成分向量）呢？我们先将问题用数学化的语言来描述。假设我们有 $n$ 个数据，数据的维度是 $p$。这 $n$ 个数据所组成的矩阵记为 $X$。$X$ 是一个 $n\times p$ 的矩阵。$X$ 的每一行代表一个数据。我们可以将矩阵 $X$ 写成
$$X=(X_1,X_2,\cdots ,X_p)$$

这里的 $X_j,1\le j\le p$ 是一个 $n\times 1$ 的列向量，表示第 $i$ 个 feature 在每一个数据点的值。为了方便起见，我们假设每一个 feature 在 $n$ 个数据点测得的值的均值为0。于是$\sum _{i=1}^n{x}_{ij}=0,\forall j=1,2,\cdots ,p$。那么，我们所要求的第一主值向量 ${\varphi }_1=({\varphi }_{11},{\varphi }_{21},\cdots ,{\varphi }_{p1}{)}^T$ 是使得线性映射
$$Z_1={\varphi }_{11}{X}_1+{\varphi }_{21}{X}_2+\cdots +{\varphi }_{p1}{X}_p$$方差最大的那个向量 [1]。 注意，这里我们须要加一个限制条件，就是 $\sum _{i=1}^p{\varphi }_{i1}^2=1$。否则，只要我们增大 ${\varphi }_{i1}$，$Z_1$ 的方差就可以变得无限大。

因为每个 $X_j$ 均为 $n\times 1$ 的向量，这里得到的 $Z_1$ 也将是一个 $n\times 1$ 的向量。我们记
$$Z_1=\left(\begin{array}{c}{z}_{11}\\ z_{21}\\ ⋮\\ z_{n1}\end{array}\right)$$。
这里 $z_{i1}$ 为 $Z_1$ 的第 $i$ 个分量 ($i=1,2,\cdots ,n$)，
$$z_{i1}={\varphi }_{11}{x}_{i1}+{\varphi }_{21}{x}_{i2}+\cdots +{\varphi }_{p1}{x}_{ip}$$。

事实上，我们可以将$$Z_1={\varphi }_{11}{X}_1+{\varphi }_{21}{X}_2+\cdots +{\varphi }_{p1}{X}_p$$ 写成矩阵的形式：$$Z_1={\varphi }_{11}{X}_1+{\varphi }_{21}{X}_2+\cdots +{\varphi }_{p1}{X}_p=X{\varphi }_1$$。

那么，$Z_1$ 的样本方差就为 $\frac{1}{n}{\sum }_{i=1}^n(Z_{i1}-\mathbb{E}(Z_1){)}^2$。$\mathbb{E}(Z_1)$ 是样本平均数。

要使得$Z_1$ 的方差最大，我们须要找到 $({\varphi }_{11},{\varphi }_{21},\cdots ,{\varphi }_{p1})$，使得 $\frac{1}{n}{\sum }_{i=1}^n(Z_{i1}-\mathbb{E}(Z_1){)}^2$ 最大。这样求解第一主成分的问题就转化成了最大化某个函数值的过程。我们注意到，
$$\begin{array}{rl}\mathbb{E}(Z_1)& =\frac{1}{n}\sum _{i=1}^n{z}_{i1}\\ & =\frac{1}{n}\sum _{i=1}^n({\varphi }_{11}{x}_{i1}+{\varphi }_{21}{x}_{i2}+\cdots +{\varphi }_{p1}{x}_{ip})\\ & =\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^p{\varphi }_{j1}{x}_{ij}\\ & =\frac{1}{n}\sum _{j=1}^p{\varphi }_{j1}\sum _{i=1}^n{x}_{ij}\end{array}$$
但是根据上面我们的约定，每一个 feature 在 $n$ 个数据点测得的值的均值为0。于是$\sum _{i=1}^n{x}_{ij}=0,\forall j=1,2,\cdots ,p$。我们就有 $\mathbb{E}(Z_1)=0$。我们的最大化问题随之变成了:
$$\underset{{\varphi }_{11},{\varphi }_{21},\cdots ,{\varphi }_{p1}}{\mathrm{maximize}}\frac{1}{n}\sum _{i=1}^n{\left(\sum _{j=1}^p{\varphi }_{j1}{x}_{ij}\right)}^2$$

可以证明，这个最大化问题的解就是矩阵 $\frac{1}{n}{X}^{T}X$ 最大的那个特征值所对应的特征向量。我们称矩阵 $\frac{1}{n}{X}^{T}X$ 是 样本矩阵 $X$ 的协方差矩阵。这个协方差矩阵是半正定的 (positive semidefinite)。所以它的特征值均是非负的。

数学证明

为什么矩阵 $\frac{1}{n}{X}^{T}X$ 最大的那个特征值所对应的特征向量就是第一主成分向量（即 ${\varphi }_1$）呢？这一部分我们将从数学上给出证明。
我们首先看要求的优化问题：
$$\underset{{\varphi }_{11},{\varphi }_{21},\cdots ,{\varphi }_{p1}}{\mathrm{maximize}}\frac{1}{n}\sum _{i=1}^n{\left(\sum _{j=1}^p{\varphi }_{j1}{x}_{ij}\right)}^2$$
我们可以将 $\frac{1}{n}\sum _{i=1}^n{\left(\sum _{j=1}^p{\varphi }_{j1}{x}_{ij}\right)}^2$ 写成一个矩阵的形式。

$\frac{1}{n}\sum _{i=1}^n{\left(\sum _{j=1}^p{\varphi }_{j1}{x}_{ij}\right)}^2=\frac{1}{n}||X{\varphi }_1|{|}^2$。回忆 $X$ 是 $n\times p$ 的矩阵，${\varphi }_1$ 是 $p\times 1$ 的列向量。而 $||X{\varphi }_1|{|}^2$ 又可以写成 ${\varphi }_1^T{X}^{T}X{\varphi }_1$。所以我们的优化问题就转化成了：
$$\underset{{\varphi }_{11},{\varphi }_{21},\cdots ,{\varphi }_{p1}}{\mathrm{maximize}}\frac{1}{n}{\varphi }_1^T{X}^{T}X{\varphi }_1=\underset{{\varphi }_{11},{\varphi }_{21},\cdots ,{\varphi }_{p1}}{\mathrm{maximize}}{\varphi }_1^T\left(\frac{1}{n}{X}^{T}X\right){\varphi }_1$$

为了证明使得 ${\varphi }_1^T\left(\frac{1}{n}{X}^{T}X\right){\varphi }_1$ 最大化的 ${\varphi }_1$ 就是 $\frac{1}{n}{X}^{T}X$ 最大的特征值对应的特征向量，我们先证明下面的引理。

Lema
如果 $A\in {\mathbb{R}}^{p\times p}$ 是一个对称的positive semidefinite 的矩阵。$A$ 的 特征值为 ${\lambda }_1>{\lambda }_2\cdots >{\lambda }_p$，对应的特征向量为 ${\varphi }_1,{\varphi }_2,\cdots ,{\varphi }_p$。那么${\varphi }_1$ 就是下面优化问题的解。
$$\underset{x\in {\mathbb{R}}^p,||x|{|}^2=1}{\max }{x}^{T}Ax$$

简要证明：
因为 $A\in {\mathbb{R}}^{p\times p}$ 是一个对称的positive semidefinite 的矩阵，我们可以将 $A$ 分解为 $A=\Phi D{\Phi }^T$。其中 $\Phi$ 是 $A$ 的特征向量组成的矩阵。即 $\Phi =({\varphi }_1,{\varphi }_2,\cdots ,{\varphi }_p)$，$A{\varphi }_i={\lambda }_i{\varphi }_i$，这里每一个 ${\varphi }_i$ 均为 $p\times 1$ 的列向量。并且 $\Phi {\Phi }^T={\mathbb{I}}_{p\times p}$。

$D$ 是由特征值 ${\lambda }_i$ 组成的对角矩阵，$$D=\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_p\end{array}\right)$$。

对于任意的列向量 $x\in {\mathbb{R}}^p,||x|{|}^2=1$，我们有
$$\begin{array}{rl}{x}^{T}Ax& =x^T\Phi D{\Phi }^{T}x\\ & =\sum _{i=1}^p{\lambda }_i{x}^T{\varphi }_i{\varphi }_i^{T}x\\ & =\sum _{i=1}^p{\lambda }_i||{\varphi }_i^{T}x|{|}^2\\ & \le \sum _{i=1}^p{\lambda }_1||{\varphi }_i^{T}x|{|}^2\\ & ={\lambda }_1\sum _{i=1}^p||{\varphi }_i^{T}x|{|}^2\\ & ={\lambda }_1||\Phi x|{|}^2\\ & ={\lambda }_1(x^T{\Phi }^T\Phi x)={\lambda }_1{x}^{T}x={\lambda }_1\end{array}$$

于是我们知道 $\underset{x\in {\mathbb{R}}^p,||x|{|}^2=1}{\max }{x}^{T}Ax\le {\lambda }_1$。如果我们取 $x={\varphi }_1$，我们有 $x^{T}Ax={\varphi }_{1}A{\varphi }_1={\lambda }_1$。所以，${\varphi }_1$ 就是最优问题 $\underset{x\in {\mathbb{R}}^p,||x|{|}^2=1}{\max }{x}^{T}Ax$ 的解。

程序验证

我们先用求特征值的方法来求主成分向量。我们的数据是有2个feature，一共有10 个数据。即 X.shape = (10, 2)。

np.random.seed(1)
m = 20
x = np.random.uniform(1, 10, m)
y = 2 * x + 1 + np.random.normal(0, 1, m)
x = x - np.mean(x)
y = y - np.mean(y)
X = np.vstack((x, y)).T # X is the data set, X.shape = (m, 2)

我们来求协方差矩阵的特征值和特征向量。

eig_vals, eig_vecs = np.linalg.eig(1 / 2 * np.dot(X.T, X))

eig_vals

array([ 1.12975274, 236.75469475])

eig_vecs # The eigenvectors are eig_vecs[:,1], eig_vecs[:, 2]

array([[-0.89631173, -0.44342449],
[ 0.44342449, -0.89631173]])

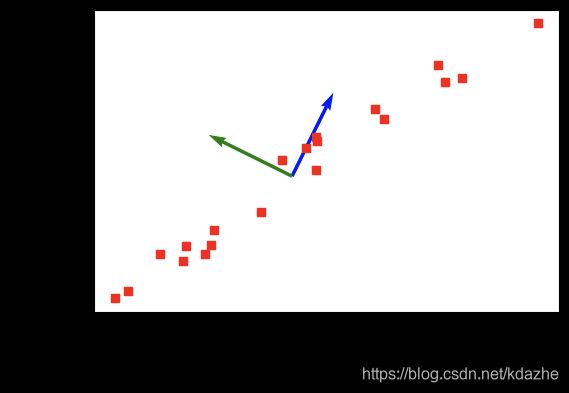
我们看到，最大的特征值是 236.75，对应的特征向量（即第一主成分）为 (-0.443, -0.896)。第二主成分为 (-0.896, 0.443)。

我们可以检验这两个主成分与用 sklearn 中的PCA 方法得到的结果是一样的。

pca = PCA(n_components=2, svd_solver='full')
pca.fit(X)
pca_phis = pca.components_

PCA(copy=True, iterated_power=‘auto’, n_components=2, random_state=None,
svd_solver=‘full’, tol=0.0, whiten=False)

array([[ 0.44342449, 0.89631173],
[-0.89631173, 0.44342449]])

可以看到，得到的第一主成分是(0.443, 0.896)，第二主成分是 (-0.896, 0.443)。这些结果与求解特征值与特征向量得到的结果相同。

原始数据 $X$（红色） 与第一主成分（蓝色）、第二主成分（绿色）如下图所示。

参考文献

[1] An introduction to statistical learning: with applications in R, Gareth James, Daniela Witten, Trevor Hastie, and Robert Tibshirani, Springer.