Pytorch总结三之 softmax回归用于分类问题

Pytorch总结三之 softmax回归用于分类问题

• 上篇博文Pytorch总结二之线性回归算法原理与实现介绍的线性回归模型适⽤于输出为连续值的情景。
• 在另⼀类情景中，模型输出可以是⼀个像图像类别这样的离散值。对于这样的离散值预测问题，我们可以使⽤诸如softmax回归在内的分类模型。和线性回归不同，softmax回归的输出单元从⼀个变成了多个，且引⼊了softmax运算使输出更适合离散值的预测和训练。本节以softmax回归模型为例，介绍神经⽹络中的分类模型。

1. softmax 回归

1.1 分类问题

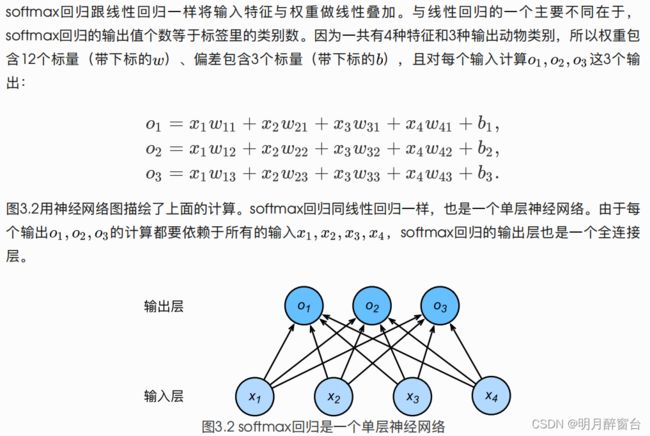
• 让我们考虑⼀个简单的图像分类问题，其输⼊图像的⾼和宽均为2像素，且⾊彩为灰度。这样每个像素值都可以⽤⼀个标量表示。我们将图像中的4像素分别记为x1, x2, x3, x4 。假设训练数据集中图像的真实标签为狗、猫或鸡（假设可以⽤4像素表示出这3种动物），这些标签分别对应离散值y1, y2, y3。
• 我们通常使⽤离散的数值来表示类别，例如y1=1, y2=2, y3=3 。如此，⼀张图像的标签为1、2和 3这3个数值中的⼀个。虽然我们仍然可以使⽤回归模型来进⾏建模，并将预测值就近定点化到1、2和3 这3个离散值之⼀，但这种连续值到离散值的转化通常会影响到分类质量。因此我们⼀般使⽤更加适合离散值输出的模型来解决分类问题。

1.2 softmax 回归模型

1.3 单样本分类的矢量计算表达式

1.4 小批量样本分类的矢量计算表达式

1.5 交叉熵损失函数

1.6 模型预测及评价

• 在训练好softmax回归模型后，给定任⼀样本特征，就可以预测每个输出类别的概率。通常，我们把预测概率最⼤的类别作为输出类别。如果它与真实类别（标签）⼀致，说明这次预测是正确的。在3实验中，我们将使⽤准确率（accuracy）来评价模型的表现。它等于正确预测数量与总预测数量之⽐。
• softmax回归适⽤于分类问题。它使⽤softmax运算输出类别的概率分布。
• softmax回归是⼀个单层神经⽹络，输出个数等于分类问题中的类别个数。
• 交叉熵适合衡量两个概率分布的差异。

2. 图像分类数据集(Fashion-MNIST)

图像分类数据集中最常⽤的是⼿写数字识别数据集MNIST。但⼤部分模型在MNIST上的分类精度都超过了95%。为了更直观地观察算法之间的差异，我们将使⽤⼀个图像内容更加复杂的数据集Fashion-MNIST（这个数据集也⽐较⼩，只有⼏⼗M，没有GPU的电脑也能吃得消）。

• 本节将使用torchvision包，他是服务于Pytorch深度学习框架的，主要用来构建计算机视觉模型。

• torchvision主要有以下几部分构成：

  [1] torchvision.datasets:一些加载数据的函数及常用的数据集接口
  [2] torchvision.models:包含常用的模型结构(含预训练模型)，例如AlexNet、VGG、ResNet等
  [3] torchvision.transforms:常用的图像变换，例如裁剪、旋转等
  [4] torchvision.utils:其他的一些有用的方法

2.1 获取数据集

注：python安装包一定要注意版本问题，安装前最好查下torch对应的其他包的版本，不然下载其他包的时候自动把torch的版本也给替换了，不过到最后一番波折后我选择了系统默认安装的cpu版torch与torchtext一起用，不然就会一直报错！！！

导入模块：

# time:20220824
# writer:yohn
#Pytorch通过softmax实现分类问题


#1.获取数据集

import torch
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import time
import sys
sys.path.append("..") # 为了导⼊上层⽬录的d2lzh_pytorch
import d2lzh_pytorch as d2l

#训练集用于模型训练得到参数，测试机用于模型验证及评价
mnist_train =torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST',
train=True, download=True, transform=transforms.ToTensor())
mnist_test =torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST',
train=False, download=True, transform=transforms.ToTensor())

#mnist_train 和 mnist_test 都是 torch.utils.data.Dataset 的⼦类
print(type(mnist_train))   #
print(len(mnist_train),len(mnist_test))   #60000 10000

#通过下标来访问任意⼀个样本,变量 feature 对应⾼和宽均为28像素的图像。由于我们使⽤了 transforms.ToTensor() ，所以每个
# 像素的数值为[0.0, 1.0]的32位浮点数。需要注意的是， feature 的尺⼨是 (C x H x W) 的，⽽不是 (H
# x W x C)。第⼀维是通道数，因为数据集中是灰度图像，所以通道数为1。后⾯两维分别是图像的⾼和宽。
feature, label = mnist_train[0]
print(feature.shape, label) # Channel x Height X Width
#torch.Size([1, 28, 28]) tensor(9)

# Fashion-MNIST中⼀共包括了10个类别，分别为t-shirt（T恤）、trouser（裤⼦）、pullover（套衫）、
# dress（连⾐裙）、coat（外套）、sandal（凉鞋）、shirt（衬衫）、sneaker（运动鞋）、
# bag（包）和ankle boot（短靴）。以下函数可以将数值标签转成相应的⽂本标签。
# 本函数已保存在d2lzh包中⽅便以后使⽤
def get_fashion_mnist_labels(labels):

    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress',
    'coat','sandal', 'shirt', 'sneaker', 'bag', 'ankleboot']
    return [text_labels[int(i)] for i in labels]

#定义一个可在一行里画出多张图像和对应标签的函数,# 本函数已保存在d2lzh包中⽅便以后使⽤
def show_fashion_mnist(images, labels):
    d2l.use_svg_display()
    # 这⾥的_表示我们忽略（不使⽤）的变量
    _, figs = plt.subplots(1, len(images), figsize=(12, 12))
    for f, img, lbl in zip(figs, images, labels):
        f.imshow(img.view((28, 28)).numpy())
        f.set_title(lbl)
        f.axes.get_xaxis().set_visible(False)
        f.axes.get_yaxis().set_visible(False)
        plt.show()

#2.显示数据及标签，看⼀下训练数据集中前9个样本的图像内容和⽂本标签。
X, y = [], []
for i in range(10):
    X.append(mnist_train[i][0])
    y.append(mnist_train[i][1])
    print(y)
    show_fashion_mnist(X, get_fashion_mnist_labels(y))

运行时，其他都没问题，只有这：

暂时还不知道该怎么解决，放张正常无异常的结果图吧，正常结果显示如下

2.2 读取小批量

# #**************读取小批量******************
#PyTorch的DataLoader 中 ⼀ 个 很 ⽅ 便 的 功 能 是 允 许 使 ⽤ 多 进 程 来 加 速 数 据 读 取 。 这 ⾥ 我 们 通 过 参
# 数 num_workers 来设置4个进程读取数据
batch_size = 256
if sys.platform.startswith('win'):
    num_workers = 0 # 0表示不⽤额外的进程来加速读取数据
else:
    num_workers = 4
train_iter = torch.utils.data.DataLoader(mnist_train,batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(mnist_test,batch_size=batch_size, shuffle=False, num_workers=num_workers)
start = time.time()
for X, y in train_iter:
    continue
print('%.2f sec' % (time.time() - start))
#1.57sec

3. softmax的从零开始实现

#3. softmax回归的从零开始实现
import torch
import torchvision
import numpy as np
import sys
sys.path.append("..") # 为了导⼊上层⽬录的d2lzh_pytorch
import d2lzh_pytorch as d2l


#1.获取数据
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

#2.初始化模型参数
# 跟线性回归中的例⼦⼀样，我们将使⽤向量表示每个样本。已知每个样本输⼊是⾼和宽均为28像素的图
# 像。模型的输⼊向量的⻓度是28*28=784 ：该向量的每个元素对应图像中每个像素。由于图像有
# 10个类别，单层神经⽹络输出层的输出个数为10，因此softmax回归的权᯿和偏差参数分别为784*10和1*10 的矩阵。
num_inputs = 784
num_outputs = 10
W = torch.tensor(np.random.normal(0, 0.01, (num_inputs,num_outputs)), dtype=torch.float)
b = torch.zeros(num_outputs, dtype=torch.float)

#同样需要模型参数梯度
W.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)

#3. 实现softmax运算
#对多为tensor按维度操作，我们可以只对其中同⼀列（ dim=0 ）或同⼀⾏（ dim=1 ）的元素求
#和，并在结果中保留⾏和列这两个维度（ keepdim=True ）。
X = torch.tensor([[1, 2, 3], [4, 5, 6]])
print(X.sum(dim=0, keepdim=True))  #tensor([[5, 7, 9]])
print(X.sum(dim=1, keepdim=True))  #tensor([[ 6],[15]])

# 在下⾯的函数中，矩阵 X 的⾏数是样本数，列数是输出个数。为了表达样本预测各个输出的概率，softmax运算会先通过 exp 函数对每个元素做指数
# 运算，再对 exp 矩阵同⾏元素求和，最后令矩阵每⾏各元素与该⾏元素之和相除。这样⼀来，最终得到的矩阵每⾏元素和为1且⾮负。因此，该矩阵每⾏
# 都是合法的概率分布。softmax运算的输出矩阵中的任意⼀⾏元素代表了⼀个样本在各个输出类别上的预测概率。
def softmax(X):
    X_exp = X.exp()
    partition = X_exp.sum(dim=1, keepdim=True)
    return X_exp / partition # 这⾥应⽤了⼴播机制

#对于随机输⼊，我们将每个元素变成了⾮负数，且每⼀⾏和为1。
X = torch.rand((2, 5))
X_prob = softmax(X)
print(X_prob, X_prob.sum(dim=1))
#tensor([[0.2206, 0.1520, 0.1446, 0.2690, 0.2138],[0.1540, 0.2290, 0.1387, 0.2019, 0.2765]]) tensor([1., 1.])

#4.定义模型
def net(X):
    return softmax(torch.mm(X.view((-1, num_inputs)), W) + b)

#5.定义损失函数
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y = torch.LongTensor([0, 2])
y_hat.gather(1, y.view(-1, 1))  #通过使⽤ gather 函数，我们得到了2个样本的标签的预测概率
#tensor([[0.1000],[0.5000]])

#交叉熵函数
def cross_entropy(y_hat, y):
    return - torch.log(y_hat.gather(1, y.view(-1, 1)))

#定义优化算法，使⽤学习率为0.1的⼩批量随机梯度下降作为优化算法
optimizer = torch.optim.SGD(net.parameters(), lr=0.1)


#6. 计算分类准确率
# 给定⼀个类别的预测概率分布 y_hat ，我们把预测概率最⼤的类别作为输出类别。如果它与真实类
# 别 y ⼀致，说明这次预测是正确的。分类准确率即正确预测数量与总预测数量之⽐。

#argmax返回每行中最大元素的索引，且返回结果与y姓黄相同
def accuracy(y_hat, y):
    return (y_hat.argmax(dim=1) == y).float().mean().item()
print(accuracy(y_hat, y))  #0.5


# 本函数已保存在d2lzh_pytorch包中⽅便以后使⽤。该函数将被逐步改进：它的完整实现将在“图像增⼴”⼀节中描述
def evaluate_accuracy(data_iter, net):
    acc_sum, n = 0.0, 0
    for X, y in data_iter:
        acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
        n += y.shape[0]
    return acc_sum / n

#为我们随机初始化了模型 net ，所以这个随机模型的准确率应该接近于类别个数10的倒数即0.1
print(evaluate_accuracy(test_iter,net))


#7.训练模型
# 训练softmax回归的实现跟“线性回归的从零开始实现” ⼀节介绍的线性回归中的实现⾮常相似。我们同
# 样使⽤⼩批量随机梯度下降来优化模型的损失函数。在训练模型时，迭代周期数 num_epochs 和学习
# 率 lr 都是可以调的超参数。改变它们的值可能会得到分类更准确的模型。
num_epochs,lr = 5,0.1

def train_ch3(net,train_iter,test_iter,loss,num_epochs,batch_size,params=None,lr=None,optimizer=None):
    for epoch in range(num_epochs):
        train_l_sum,train_acc_sum,n=0.0,0.0,0
        for x,y in train_iter:
            y_hat=net(x)
            l=loss(y_hat,y).sum()

            #梯度清零
            if optimizer is not None:
                optimizer.zero_grad();
            elif params is not None and params[0].grad is not None:
                for param in params:
                    param.grad.data.zero_()

            l.backward()
            if optimizer is None:
                d2l.sgd(params,lr,batch_size)
            else:
                optimizer.step()

            train_l_sum += l.item()
            train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
            n += y.shape[0]
        test_acc = evaluate_accuracy(test_iter, net)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'% (epoch + 1, train_l_sum / n,
            train_acc_sum / n,test_acc))
#开始训练
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs,batch_size, [W, b], lr)
# epoch 1, loss 0.7853, train acc 0.751, test acc 0.794
# epoch 2, loss 0.5692, train acc 0.814, test acc 0.811
# epoch 3, loss 0.5257, train acc 0.826, test acc 0.814
# epoch 4, loss 0.5007, train acc 0.833, test acc 0.823
# epoch 5, loss 0.4866, train acc 0.836, test acc 0.827

#8.预测
X, y = iter(test_iter).next()
true_labels = d2l.get_fashion_mnist_labels(y.numpy())
pred_labels =d2l.get_fashion_mnist_labels(net(X).argmax(dim=1).numpy())
titles = [true + '\n' + pred for true, pred in zip(true_labels,pred_labels)]
d2l.show_fashion_mnist(X[0:9], titles[0:9])

result: