基于MPS算法和改进的非支配排序遗传算法II（MNSGA-II）求解配备起重机的模糊鲁棒设施布局问题（Matlab代码实现）

 ‍个人主页：研学社的博客 

欢迎来到本博客❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

本文目录如下：

目录

1 概述

2 运行结果

3 Matlab代码实现

4 参考文献

---

1 概述

本文用了NSGA-II的改进优化算法——MNSGA-II

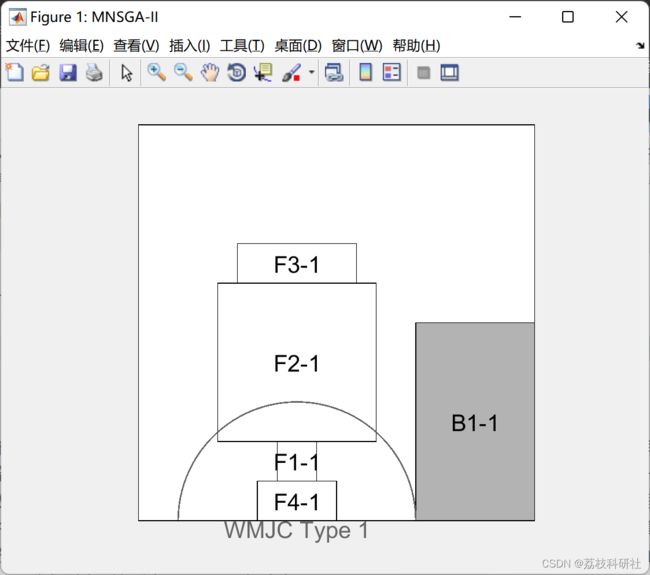
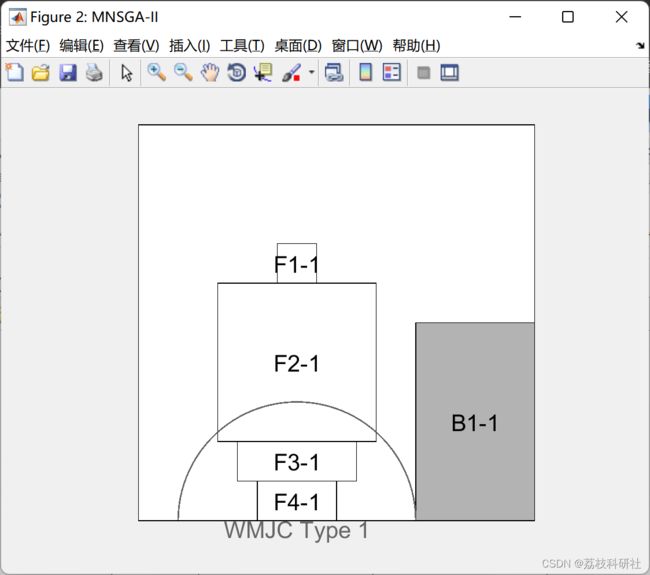
设施布局问题定义为在工厂区域中放置设施。本文通过设施尺寸阐明了设施布局问题，设施之间的物料流动不确定为模糊随机变量，厂区配备了壁挂式旋臂起重机和小型闸门起重机，厂区存在一些禁止放置设施的禁区。这些问题的目标功能被认为是最大限度地减少操作员和起重机的材料处理成本，并通过计算壁挂式旋臂起重机和小型闸式起重机在设施上的覆盖面积，首次最大限度地提高起重机的可用性。为了解决这个问题，提出了一种改进的非支配排序遗传算法II（MNSGA-II）。 此代码呈现测试用例 1 并通过 MNSGA-II 解决它。

2 运行结果

 

 

 

部分代码：

%% NSGA-II Main Loop

for it=1:MaxIt
    
    % Crossover
    popc=repmat(empty_individual,nCrossover/2,2);
    for k=1:nCrossover/2
        notryc=0;
        i1=randi([1 nPop]);
        p1=pop(i1);
        
        i2=randi([1 nPop]);
        p2=pop(i2);
        
        [popc(k,1).Position,popc(k,2).Position]=ApplySwap(p1.Position,p2.Position,model);
        
        while (isFeasible(popc(k,1).Position,model)==false || isFeasible(popc(k,2).Position,model)==false) && notryc             notryc=notryc+1;
            [popc(k,1).Position,popc(k,2).Position]=ApplySwap(p1.Position,p2.Position,model);
        end
        if notryc==a
            popc(k,1).Position=p1.Position;
            popc(k,2).Position=p2.Position;
        end
        popc(k,1).Cost=CostFunction(popc(k,1).Position,model);
        popc(k,1).MHO_Cost=popc(k,1).Cost.MHO_Cost;
        popc(k,1).MHC_Cost=popc(k,1).Cost.MHC_Cost;
        popc(k,1).Crane_Usability=Score( popc(k,1).Position,model);
        popc(k,1).CostTotal=popc(k,1).MHO_Cost+popc(k,1).MHC_Cost-popc(k,1).Crane_Usability;
        
        popc(k,2).Cost=CostFunction(popc(k,2).Position,model);
        popc(k,2).MHO_Cost=popc(k,2).Cost.MHO_Cost;
        popc(k,2).MHC_Cost=popc(k,2).Cost.MHC_Cost;
        popc(k,2).Crane_Usability=Score(popc(k,2).Position,model);
        popc(k,2).CostTotal= popc(k,2).MHO_Cost+ popc(k,2).MHC_Cost- popc(k,2).Crane_Usability;
        
        
    end
    popc=popc(:);
    
    % Mutation
    popm=repmat(empty_individual,nMutation,1);
    for k=1:nMutation
        notrym=0;
        i=randi([1 nPop]);
        p=pop(i);
        
        popm(k).Position=CreateNeighbor(p.Position,model,ActionList);
        while isFeasible(popm(k).Position,model)==false && notrym             notrym=notrym+1;
            popm(k).Position=CreateNeighbor(p.Position,model,ActionList);
        end
        if notrym==a
            popm(k).Position=p.Position;
        end
        popm(k).Cost=CostFunction(popm(k).Position,model);
        popm(k).MHO_Cost=popm(k).Cost.MHO_Cost;
        popm(k).MHC_Cost=popm(k).Cost.MHC_Cost;
        popm(k).Crane_Usability=Score(popm(k).Position,model);
        popm(k).CostTotal=popm(k).MHO_Cost+popm(k).MHC_Cost-popm(k).Crane_Usability;
        
    end
    
    % Merge
    pop=[pop
        popc
        popm];
    
    % Non-Dominated Sorting
    [pop,F]=NonDominatedSorting(pop);
    
    % Calculate Crowding Distance
    pop=CalcCrowdingDistance(pop,F);
    
    % Sort Population
    [pop,~]=SortPopulation(pop);
    
    % Truncate
    pop=pop(1:nPop);
    
    % Non-Dominated Sorting
    [pop,F]=NonDominatedSorting(pop);
    
    % Calculate Crowding Distance
    pop=CalcCrowdingDistance(pop,F);

3 Matlab代码实现

4 参考文献

部分理论来源于网络，如有侵权请联系删除。

Soroush Esmikhani, Hamed Kazemipoor, Farzad Movahedi Sobhani, Seyyed Mohammad Hadji Molana (2022)