【对抗攻击论文笔记】Decision-Based Adversarial Attack With Frequency Mixup
文章目录
- Motivation
- Contributions
- Method
-
- 1.boundary detection
- 2. f-mixup
- 3.f-attack
- 4. frequency binary search
- Result
Motivation
首先基于决策的攻击通常会进行过多的查询,这样就导致了攻击容易被发现,另外很多攻击无法有效地绕过检测。所以本文的目的就是研究更隐蔽和查询效率更高的基于决策的攻击。
其次,我们知道自然图像的傅里叶光谱大部分集中在低频域 ,CNN 提取的特征其实涉及不同频率的信息。同时,有文章提到人类视觉系统(HVS)对高频分量的敏感度低于低频分量。也就是说卷积神经网络 (CNN) 和人类视觉系统 (HVS) 工作机制存在差异性。所以从这一点出发,其实就是本文攻击方法的idea,如果保持低频分量不变而只修改高频分量,HVS 由于其不敏感几乎不会感知到任何变化,但 CNN 可能会做出错误的预测。
Contributions
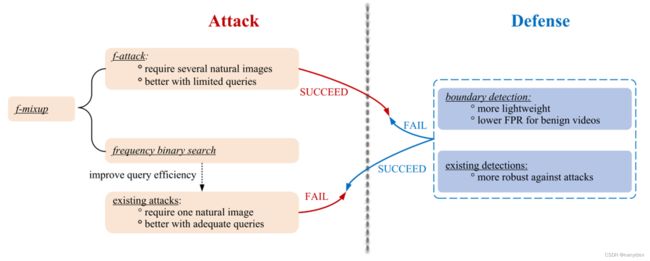
看一下本文的主要贡献,这张图是从防御和攻击两个角度出发。
首先,我们先看右边,从防御者的角度本文设计了一种轻量级检测方法:boundary detection(边界检测),如果某些用户在目标模型的决策边界附近进行了过多的查询,边界检测就会将这种行为识别为攻击,这种检测的成功性揭示了现有基于决策攻击方法的局限性。
然后再从攻击的角度,那既然本文提出了新的检测方法,就必须开发出更强大的攻击,所以提出了f-attack的攻击方法,首先以 f-mixup 为核心,在频域中生成高质量的候选对抗样本,然后将这些候选者依次输入到目标模型中,直到目标模型做出错误预测。当查询受到严重限制时, f-attack 既可以成功绕过检测,又可以实现非常好的性能。
本文还引入了基于 f-mixup 的频率二分搜索(frequency binary search),作为现有基于决策的攻击的plug-and-play(即插即用)模块,以进一步提高其查询效率。
Method
1.boundary detection
首先从防御者角度讲一下了边界检测(boundary detection),一般来说在基于决策的攻击中,攻击者必须频繁地在目标模型的决策边界附近进行查询,否则它将始终输出相同的类标签。之前提出的一些检测效果已经很好了,但它们消耗了太多资源来存储历史查询或者是计算查询之间的相似性。
为了解决这些缺点,本文提出了边界检测,它将在决策边界附近提供一系列查询的行为识别为攻击。那具体是怎么做的呢,边界检测使用置信度最高的两个类别之间的ambiguity也就是模糊性来衡量距离,令 $Δ(x)=p1(x)-p2(x)$ , p1(x)和p2(x)分别是top-1和top-2的概率,首先边界检测会维护一个长度为n的先入先出的队列,每当用户输入一个查询时,边界检测计算相应的模糊值并添加到队列末尾,边界检测会将队列中的每个元素和阈值 ϵ p \epsilon_p ϵp 相比,如果至少有k个模糊值小于 ϵ p \epsilon_p ϵp,那就认为是攻击。
2. f-mixup

攻击方法f-attack,首先讲下这个方法的核心f-mixup,用来产生候选的对抗样本。按照之前的motivation,如果我们用参考样本的对应部分替换干净样本的中高频部分,这样更有可能误导目标模型做出错误的预测。
所以这个图的意思就是这样,首先将clean example(干净样本) x 0 x_0 x0 和reference example(参考样本) x i x_i xi 进行傅里叶变换,并对他们进行了中心化处理(也就是把低频分量向中心移动,高频分量向两边移动),然后将他们俩分别通过带通和带阻滤波器,再把他们mix也就是相加一下,最后进行傅里叶反变换就得到了对抗样本,从图中可以看到,这个对抗样本和之前的干净样本从直观上几乎一样,但是如果将他输入到分类器中输出就会误判。
(作者在文中还进行了公式推导和分析)
x 0 x_0 x0的对抗样本可以写成: x ~ 0 i = x 0 b s + x i b p \tilde{x}_{0i}=x_0^{bs}+x_i^{bp} x~0i=x0bs+xibp 这个 x 0 b s x_0^{bs} x0bs就等于被攻击图片通过带阻滤波器后的傅里叶反变换, x i b p x_i^{bp} xibp就等于攻击图片通过带通滤波器的傅里叶反变换
modified f-mixup
最后的f-attack没有采用上述的f-mixup,而是对它做了一定的修改。因为考虑到上述的f-mixup是从参考集中提取特定频率,但是由于从不同参考集中提取的分量的能量差异很大,这样就无法控制生成的候选对抗样本的distortion(失真)。他具体修改是这样的,对之前的公式9引入一个系数k,就成了公式15,现在就是 x ~ 0 i = x 0 b s + k x i b p \tilde{x}_{0i}=x_0^{bs}+kx_i^{bp} x~0i=x0bs+kxibp令 p 0 i = k x i b p − x 0 b p p_{0i}=kx_i^{bp}-x_0^{bp} p0i=kxibp−x0bp,这就是一个对抗扰动,令扰动距离 ∣ ∣ p 0 i ∣ ∣ = ρ ||p_{0i}||=\rho ∣∣p0i∣∣=ρ,则k可以根据余弦定理进行计算。

3.f-attack
接下来就是f-attack,既提高了查询效率又可以绕过检测。具体是这样的:给定一个标记为 y 的干净样本 x0,distortion的阈值是ρ,查询预算为n,假设攻击者拥有 n 个自然图像 {x1, . . . , xn} 构成参考集。设置上限截止频率 rh 后,f-attack 执行以下步骤:
(1) 通过在[0, rh]中进行二分查找直到||x0bp|| ≈ 0.7ρ来确定下限截至频率rl,
(2) 在 x0 和每个参考集之间执行修改的 f-mixup 以生成 n 个候选
(3) 将这些候选集连续输入目标模型,直到它做出错误的决定或攻击者用完查询预算。
那么为什么f-attack能绕过检测呢,因为现存的基于决策的攻击必须在边界点周围轻微扰动目标模型,因此它们很容易被检测到。相比之下,f-attack 直接产生多个具有特定失真的候选对抗样本。因此,目标模型将接收彼此足够远的样本序列,并且这些查询的中心是自然图像而不是边界点。
文中还提出,这样的f-attack还是有一定缺点的,比如这样的攻击比如需要手动收集参考集,,另外不合适的rh可能会影响攻击性能所以进一步提出动态的f-attack,只需要使用单个参考样本,动态 f-attack 通过不同的 rh 生成多个候选者。
4. frequency binary search
为了绕过检测,f-attack 丢弃了传统的基于决策的攻击使用的模型反馈。因此,它的性能不会随着查询的增加而显着提高。因此,如果攻击者有相对充足的查询预算并且目标模型没有配备检测功能,则 f-attack 不是一个明智的选择。对于这种情况,文章为现有的基于决策的攻击引入了plug-and-play(即插即用)频率二分搜索,配备频率二分搜索,大多数现有的基于决策的攻击可以获得更令人满意的初始化,并在后续迭代中避免局部最优,从而显著且持续地提高查询效率。

在算法 1 中,给定一个干净的样本 x 和一个对抗样本 x ~ \tilde{x} x~,频率二分搜索将对抗样本更新为 x r ~ = f − m i x u p ( x , x ~ ; 2 , r ) \tilde{x_r} = f-mixup(x, \tilde{x}; \sqrt2, r) xr~=f−mixup(x,x~;2,r) 其中通过二分搜索确定[0, √2]。配备频率二分搜索,大多数现有的基于决策的攻击变得更加查询高效。
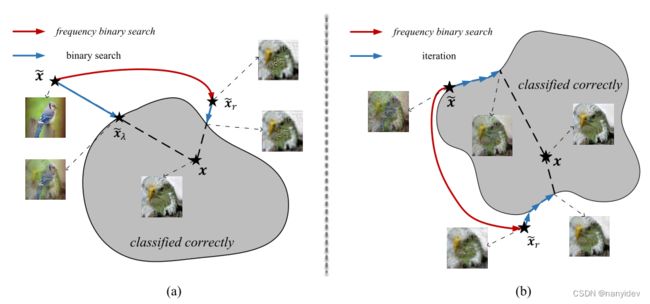
(a)引入频率二分搜索,攻击者可以找到比一开始单独二分搜索获得的边界点质量更高的边界点
通过在迭代过程中进行频率二分搜索,攻击避免了局部最优,如图 8(b) 所示。现有的基于决策的攻击通常会迭代地更新其邻域内的当前对抗样本,因此攻击倾向于收敛到局部最优。为了克服这个限制,我们在每 k 次迭代后执行频率二进制搜索。
Result
result-1
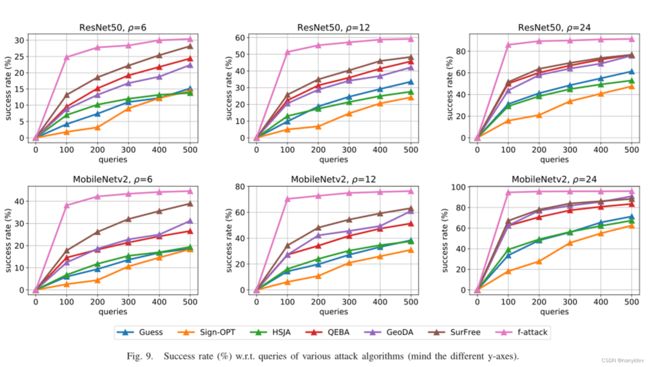
最后我们看一下实验结果,首先看到图9,对 ResNet50 和 MobileNetv2 执行untargeted(非定向)攻击,将 f-mixup 攻击与 ImageNet 上基于决策攻击的SOTA比较。考虑了六种基于决策的攻击:Guess [40]、Sign-OPT [35]、HSJA [36]、QEBA [37]、GeoDA [38] 和 SurFree [41]。可以看到f-attack 在攻击成功率上超过了其他算法,并且查询更少。
result-2
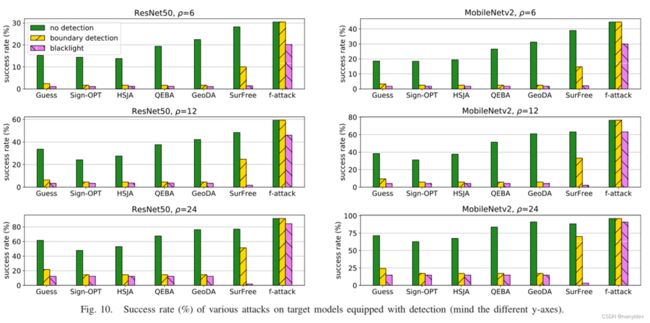
然后图10第二个实验结果是为了验证每种攻击对检测的性能。首先横轴代表的是不同的攻击方法,纵轴是攻击的成功率,如果是没有检测,那大家的成功率都比较高,现在就是比较有boundary detection和Blacklight检测的情形,比如我们先看边界检测,结果表明之前的很多方法都不能攻击成功,但是本文的f-attack还是可以攻击成功。所以Blacklight 和边界检测都可以有效防御除 f-attack 之外的基于决策的攻击。
result-3
最后是作者做的一些对比实验,首先是表4,考虑到了不同的变换,除了DFT变换,还有DCT,B-DCT,DWT这些变换。可以发现DCT 略好于 DFT。但由于 DFT 是最基本的变换,可以快速实现。
表7就是上面提到的动态的f-attack,主要是为了减少所需参考样本的数量,并让不合适的RH的不利影响最小。对于单个参考示例,动态f-攻击将Rh分别设置为1、0.75、0.6、0.5、0.43以生成5个候选。因此,要进行500个查询,动态f-攻击只需要100个参考示例。表中给了不同RH下的普通f-攻击与动态f-攻击的比较。在失真较小的情况下,动态f-攻击虽然需要较少的参考实例,但其成功率最高。设置Rh后,f-Attack只能修改特定频率。相比之下,动态f攻击可以动态地改变rh,从而可以在更宽的频率范围内修改特征,从而获得更好的性能。