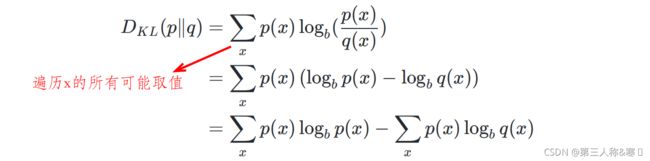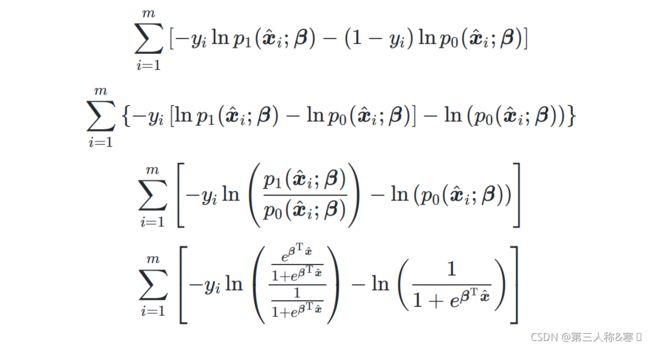机器学习-对数几率回归
目录
前言
一、对数几率回归的机器学习三要素
二、对数几率回归
2.1 算法原理
2.1.1 广义线性模型
2.1.2 对数几率回归
2.2 利用极大似然估计推导损失函数
2.2.1 确定概率密度（质量）函数
2.2.2写出似然函数
2.3 利用信息论推导损失函数
2.3.1基本概念
2.3.2 利用“交叉熵最小化"
总结
前言
与一元线性回归、多元线性回归任务不同，此文中涉及到的对数几率回归，意在实现分类任务，对比回归任务意在预测实际的数值。思路均来源于周志华老师《机器学习》3.3节的内容。
一、对数几率回归的机器学习三要素
1.模型：根据具体问题，确定假设空间——此篇为线性模型，输出值范围为[0,1]，为近似阶跃的单调可微函数；
2.策略：根据评价标准，确定选取最优模型的策略（通常会产生一个“损失函数”）——此篇由最大似然估计法、信息论来确定损失函数最小的等价条件；
3.算法：求解损失函数，确定最优模型——可以采用梯度下降、牛顿法近似求解。
二、对数几率回归
2.1 算法原理
2.1.1 广义线性模型
对于线性模型，虽然简单直接，但有很多种变化。对于样例
,
：
①第三章前半部分我们希望线性模型的预测值逼近真实标记
时，得到了线性回归模型：
;
②同样也可以令模型的预测值逼近的衍生物：认为示例对应的输出标记是在指数尺度上的变化，则可将输出的对数作为线性模型逼近的目标：
,即为 “对数线性回归”。
实际上是让
b逼近，形式上为线性回归，但实质上是在求取输入空间到输出空间的非线性函数映射，此时对数函数起到了将线性模型的预测值与真实标记联系起来的作用。
更一般的，考虑单调可微函数
，令
，对应为“广义线性模型”，其中为“联系函数”。
2.1.2 对数几率回归
在线性模型的基础上套一个映射函数来实现分类功能。根据广义线性模型的概念，需要找一个单调可微的函数将分类任务的真实标记与线性回归模型的预测值联系起来。
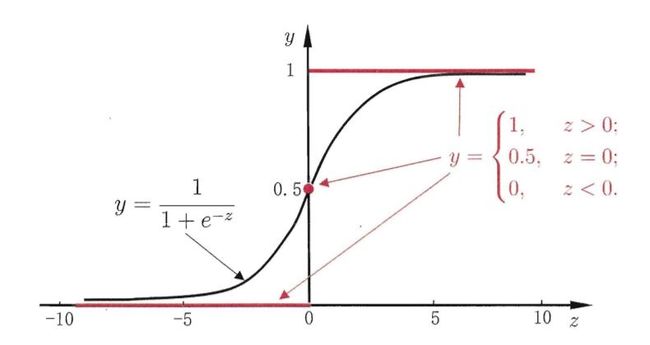
考虑二分类任务，采用的映射函数如下图示意：
在对数几率函数的映射下，
，
。
进行对数处理：
。
将
作为样本
作为正例的可能性，则
为其作为反例的可能性，其比值
称为“几率”，反映了作为正例的相对可能性，则
即为“对数几率”。
这种通过对数几率回归函数映射的分类学习方法，有以下优点：
①直接对分类可能性进行建模，无需事先假设数据分布，避免了假设分布不准确的问题；
②不仅预测出“类别”，而是得到近似概率预测，对概率辅助决策的任务很有用；
③在下述计算过程中，我们会发现目标函数是任意阶可导的凸函数，有很好的数学性质，现有的许多数值优化算法都可直接用于求取最优解。
2.2 利用极大似然估计推导损失函数
2.2.1 确定概率密度（质量）函数
对于，将视为类后验概率估计
，代入原式可解出：
； 
。
为了便于讨论，令
，
，则上式可简写为：
；
。
所谓概率密度函数，指描述随机变量输出值在某个确定的取值点附近的可能性的函数。由上述概率取值可推得随机变量的概率密度（质量）函数为：
。
2.2.2写出似然函数
代入
，
：
由于
，则代入两种取值可得：
综合两式，可得对数似然函数的等价形式：
对于损失函数，习惯以最小化为目标，故可将“最大化
等价为最小化
。
2.3 利用信息论推导损失函数
2.3.1基本概念
①信息论：以概率论、随机过程为基本研究工具，研究广义通信系统的整个过程。
②自信息：用来衡量单一事件发生时所包含的信息量多寡。
，
时，单位为bit；当
时单位为
。
③信息熵（自信息的期望值）：用于度量随机变量
的不确定性，信息熵越大越不确定。
![H(X)=E\left [ I(X) \right ]=-\sum_{x}^{}p(x)log_{b}p(x)](http://img.e-com-net.com/image/info8/4500d4215bee4f899d0df92a73af3820.gif){kind=small}
（以离散型为例）
约定：若
，则
，此时对应为确定性问题。
④相对熵（KL散度）：度量两个分布的差异，其典型使用场景是用来度量理想分布
和模拟分布
之间的差异。
其中，
称为交叉熵，理想分布是未知但固定的分布（频率学派角度），对应为
常量，则最小化相对熵等价于最小化交叉熵。
2.3.2 利用“交叉熵最小化"
交叉熵对应为：
，代入
与
得到对应的交叉熵表达式：
通常令，则转化为最小化：
对于全体训练样本，总体的交叉熵为各个部分交叉熵之和：
化简后的表达式为：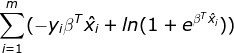
，与用极大似然估计推导对数似然函数后得到的等价最小条件的公式相同！
总结
以上思路来源于《机器学习》这本书3.3节的内容，对数几率回归属于在一元和多元线性回归问题基础上的拓展，为本书中的重点内容，公式推导过程复杂但基本思路与前半章相同，条理清晰，需要耐心。内容仅代表个人的思路和理解，如有错误欢迎指正！