图像二值化处理(全局阈值 自适应阈值 手动阈值操作以及直方图画法)

图像二值化处理

二值化原理

图像二值化就是把让图像的像素点只有0和1（只有黑白两各种颜色,黑是背景，白是前景），关键点是寻找一个阈值T，使图像中小于阈值T的像素点变为0，大于T的像素点变为255。下面介绍的就是寻找一个图像的阈值T的方法。（主要根据直方图）

API介绍

retval = cv2.threshold(src, des, thresh, maxval, type)

• retval：返回的阈值（double类型）
• dst：阈值分割结果图像(也可以写到函数参数里面)
• src：原图像， 可以是多通道的
• thresh：要设定的阈值
• maxval：当type类型是THRESH_BINARY时，需要设定的最大值
• type：阈值分割的方式(也正是type的不同导致了有多种方法)

手动设置阈值

均值法

利用图像像素点的平均值作为二值化处理的阈值。需要手动找到图像像素点的平均值，然后作为API的阈值传入，代码如下：

  #include
    #include
    
    using namespace std;
    using namespace cv;
    
    int main()
    {
    	Mat src = imread("C:\\Users\\86151\\Desktop\\opencv\\picture\\4.jpg");
    	Mat src_gray;//装灰度图像
    	Mat src_thres;//来装二值化的图像
    	if (src.empty())
    	{
    		cout << "no picture" << endl;
    		return -1;
    	}
    	imshow("src", src);
    	//对图像进行灰度处理
    	cvtColor(src, src_gray, COLOR_BGR2GRAY);
    	imshow("GRAY", src_gray);
    	//得到像素点平均值
    	Scalar m = mean(src_gray);//mean函数就是求图像像素点平均值的函数，返回值是Scalar类型
    	//进行二值化处理
    	threshold(src_gray, src_thres, m[0], 255, THRESH_BINARY);//255是最大值
    	imshow("threshold", src_thres);
    	waitKey(0);
    	return 0;
    }

二值化效果如下：

迭代法

迭代法是均值法的升级版：

1.选取初试分割阈值，一般初始为图像灰度值的平均值T

2.根据阈值T将图像分割为前景和背景（大于阈值为前景，小于为背景），分别求出两者的平均值T0和T1

3.计算新阈值T2 = （T0 + T1）/ 2

4.若T == T2,那么最终阈值就是T2，否则T = T2，再次从2开始。

代码如下：

T=img.mean()

def ThresholdIteration(T,img):
    while True:
        T0=img[img>T].mean()
        T1=img[img<=T].mean()
        t=(T0+T1)/2
        if T==t:
            return T
        else:
            T=t
T=int(ThresholdIteration(T,img))
th,img_bin = cv.threshold(img,T,255,cv.THRESH_BINARY)
print(f'Thrshold is {th}')
show(np.hstack([img,img_bin]))

自动设置阈值

直方图法

直方图法就是默认阈值参数是125，适合于双峰直方图图像，代码如下：

   #include
    #include
    
    using namespace std;
    using namespace cv;
    
    int main()
    {
    	Mat src = imread("C:\\Users\\86151\\Desktop\\opencv\\picture\\4.jpg");
    	Mat src_gray;
    	Mat src_thres;
    	if (src.empty())
    	{
    		cout << "no picture" << endl;
    		return -1;
    	}
    	imshow("src", src);
    	//对图像进行灰度处理
    	cvtColor(src, src_gray, COLOR_BGR2GRAY);
    	imshow("GRAY", src_gray);
    	//得到像素点平均值
    	Scalar m = mean(src_gray);
    	//进行二值化处理
    	threshold(src_gray, src_thres, 125, 255, THRESH_BINARY);//更改的地方
    	imshow("threshold", src_thres);
    	waitKey(0);
    	return 0;
    }

结果如下：

全局阈值法

OTSU法

OTSU法是现在最常用也是准确度较高的算法：区别就是再threshold函数的type中加上关键词即可，阈值处手动设置为0，代码如下：

  threshold(src,des,0,255,THRES_BINARY | THRES_OTSU)

原理如下：
假设一个图像的直方图如图所示（原本前景、背景像素直方图是一个图，假设2为阈值的话就会区分前景和背景，如图所示，这是假设的情况，后续opencv会从0到5这留个区间都假设一遍）

opencv要计算的对象有背景像素直方图和前景像素直方图，两者横区间是0 1 2 3 4 5这六区间。

首先面对背景像素直方图：

1.opencv计算权重W = （8 + 7 + 2）/ 36，36是整个直方图(包括前景和后景)的像素值的和，根据图像可以计算出这六个数字相加为36。

2.计算 0 1 2这三个区间的加权平均值u = （0 * 8 + 1 * 7 + 2 * 2 ）/ 17 = 0.6471。

3.计算背景像素直方图的方差：
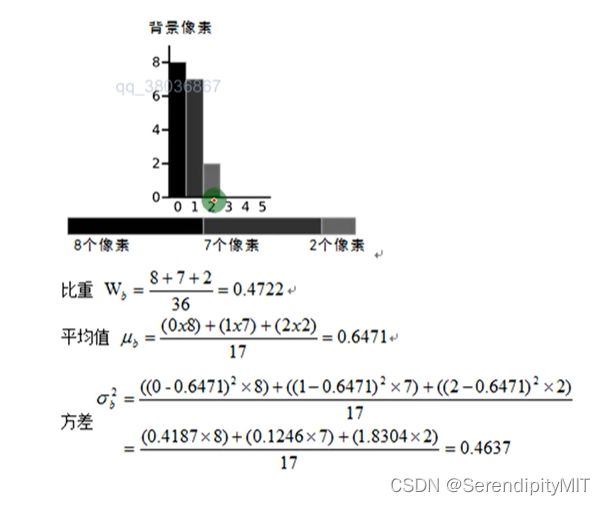至此，背景像素直方图计算完毕，按照同样的方法计算前景像素直方图：

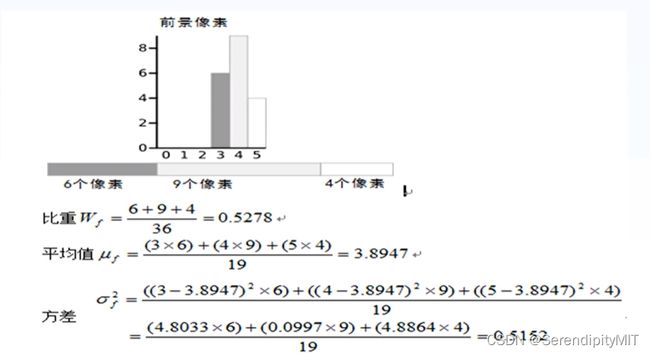
然后按照两图的权重和方差进行权重运算（类内方差）：

得到一个最终数值。这只是假设2为阈值的情况，实际上opencv会从0 - 5都假设一遍，都计算出这样的最后结果，

选取结果最小的点作为实际的阈值。这就是OTSU算法查找阈值的原理。

实际结果（代码换掉threshold函数这一行就可以了）：

三角形法

三角形法适应于单峰直方图，若图像直方图如下（蓝色的线）：

那么三角形法就是选择直方图的最低点和最高点连一条线，然后在直方图的边上找一点使之距离我们所画的这一条线最远，标记为点O，那么点O的横坐标就是实际的阈值，效果如下：

代码如下：

threshold(src,des,0,255,THRES_BINARY | THRES_TRIANGLE)

自适应阈值法

有时候一张图片有些地方很暗，有些地方很亮，那样继续使用全局阈值的话，会导致图像二值化不合理，比如：

使用OTSU算法处理后的二值化图像，可见有些部分变黑了，这不是我们想要的结果，这个时候就要用到自适应阈值处理方法了，自适应阈值分割则将图像分成很多个小块，对每个小块单独计算其阈值，然后用这个计算得到的阈值对该小块进行分割，这样的好处是，即使受到光照影响，某一块较暗或较亮，但是可以单独计算这一块的合理阈值来进行分割而不用使用全局的固定阈值，换句话说，亮的小块对应的阈值较大，暗的小块对应的阈值较小，从而可以达到很好的分割效果。

API

adaptiveThreshold( src, des,maxValue, adaptiveMethod, thresholdType, blockSize, C[, dst])
第一个参数：InputArray类型的src，输入数组，必须为单通道，8位或32位的浮点型Mat即可。
第二个参数：OutputArray类型的dst，与输入有一样的尺寸和类型。
第三个参数：double类型的maxval，给像素赋的满足条件的非0值。
第四个参数：int类型的adaptiveMethod，指定要使用的自适应阈值算法，可取值为ADAPTIVE_THRESH_MEAN_C或ADAPTIVE_THRESH_GAUSSIAN_C
第五个参数：int类型的thresholdType，阈值类型，必须为THRESH_BINARY或THRESH_BINARY_INV。
第六个参数：int类型的blocksize，用于计算阈值大小的一个像素的邻域尺寸，取3，5，7等。
第七个参数：double类型的C，减去平均或加权平均值后的常数值，通常为正数。

使用代码如下：

 adaptiveThreshold(src_gray, src_thres, 255, ADAPTIVE_THRESH_GAUSSIAN_C, THRESH_BINARY, 7, 4);//注意：输入是灰度图像

效果如下：

绘制图像直方图

  #include
    #include
    
    using namespace std;
    using namespace cv;
    
    int main()
    {
    	Mat src = imread("C:\\Users\\86151\\Desktop\\opencv\\picture\\4.jpg");
    	Mat src_gray;
    	if (src.empty())
    	{
    		cout << "no picture" << endl;
    		return -1;
    	}
    	imshow("src", src);
    	cvtColor(src, src_gray, COLOR_BGR2GRAY);
    	imshow("GRAY", src_gray);
    	//绘制直方图
    	Mat src_hist;
    	const int a = 256;
    	float bin_range[2] = { 0,255 };
    	const float* range[1] = { bin_range };
    	calcHist(&src_gray, 1, 0, Mat(), src_hist, 1, &a, range, true, false);
    	//绘制直方图的画布
    	int hist_w = 500;
    	int hist_h = 400;
    	int hist_bin = cvRound((double)hist_w / a);
    	Mat hist_canvas = Mat::zeros(hist_h, hist_w, CV_8UC3);
    	//对直方图数据进行归一化
    	normalize(src_hist, src_hist, 0, 255, NORM_MINMAX, -1, Mat());
    	//将直方图以折线统计图的方式花在画布上
    	for (int i = 1; i < 256; i++)
    	{
    		line(hist_canvas, Point(hist_bin * (i - 1), hist_h - cvRound(src_hist.at<float>(i - 1))),
    			Point(hist_bin * (i), hist_h - cvRound(src_hist.at<float>(i))), Scalar(255, 0, 0), 2, 8, 0);
    	}
    	imshow("src_hist", hist_canvas);
    	waitKey(0);
    	return 0;
    }

结果如图：

SERENDIPITY