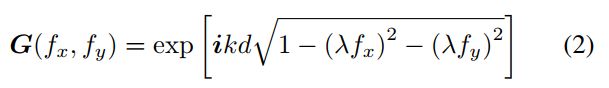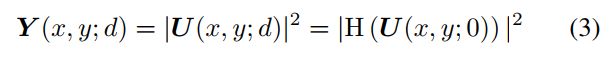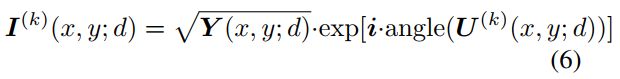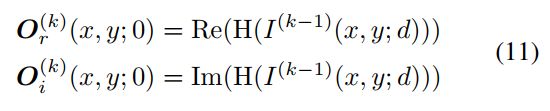Physics-based Iterative Projection Complex Neural Network for Phase Retrievalin Lensless Microscopy

摘要

从强度测量中提取相位在许多真实世界的成像任务中起着核心作用。 近年来，基于深度神经网络的相位检索方法层出不穷，并显示出良好的性能。 然而，它们的可解释性和泛化性仍然是一个主要的挑战。 本文提出将基于模型的备选投影方法和深度神经网络的优点结合起来进行相位检索，从而同时实现网络的可解释性和推理有效性。 具体地说，我们将备选投影相位检索的迭代过程展开为一个前馈神经网络，其层模拟处理流程。 成像过程的物理模型自然地嵌入到神经网络结构中。 此外，提出了一种复值u网，用于定义对偶平面正、反投影的先验图像。 最后，我们将基于物理的公式指定为未经训练的深度神经网络，其权重被强制适应给定的强度测量值。 总之，我们的相位恢复方案是有效的，可解释的，基于物理的和无监督的。 实验结果表明，该方法在实际的相位检索应用于无透镜显微成像方面取得了较好的性能。  

1、简介

在实际成像系统中的光学探测器，如CCD和CMOS，只能测量电磁波的大小(亮度或强度)。 相位检索(Phase retrieval, PR)，又称相位成像，是指从强度测量中恢复检测过程中丢失的相位信息。 它在科学和工程的许多应用中起着至关重要的作用，包括计算显微术，定量相位成像，x射线晶体学，计算机生成全息术等。  

由于光学相位不能由电子探测器直接测量，因此需要采用相位恢复算法。 多年来，人们提出了许多解决相位恢复问题的方法。 目前最流行的相位检索方法是基于可选投影的方法，该方法由Gerchberg和Saxton首创，Fienup进行了扩展。 另一种投影算法旨在从两个不同平面(样本物体平面和相机传感器平面)的幅值测量恢复复杂图像。 它从随机的初始估计开始，迭代应用双平面投影:在每次迭代时，将当前估计投影到像平面，使其频谱的大小与观测值相匹配; 然后将信号投影到目标平面，以符合其结构的一些先验知识。

另一类方法是利用现代优化理论的工具来开发相位恢复算法。 相位恢复是一个NP困难的问题。 从组合优化的角度来看，半定规划是解决这一问题的有力工具。 Candes等人的将相位检索描述为一个矩阵补全问题，该问题通过将多个结构化照明与凸规划的思想相结合来解决。 Waldspurger等人将相位检索问题视为复相位向量上的非凸二次规划，并提出了类似于经典MaxCut半定规划的易于处理的松弛。 然而，基于SDP的算法的计算复杂度随着信号维数的增加而急剧增加。 此外，它需要非常大的内存来进行计算。 因此，在实际应用中，沿着这条线的算法通常应用于一维信号。   

近年来，用于相位检索的深度学习方法越来越受欢迎。 Rivenson等人[21]率先提出了将深度学习应用于相位检索的方法，该方法以端到端方式进行相位检索。 在[14]中，Metzler等人提出利用正则化去噪框架和基于卷积神经网络的去噪来进行相位检索。 Hyder等人[9]提出利用少量训练图像学习参考信号，进一步利用梯度下降展开网络辅助解决傅立叶相位检索问题。 以上方法都是在监督的方式下工作的，其中深度神经网络是通过最小化地面真实值和观测值之间的损失函数来训练的。 然而，在许多成像场景中，很难甚至不可能获得足够数量的地面真实图像进行训练。 此外，这些方法没有考虑成像物理，使得网络既需要学习物理测量的形成，又需要学习相位重建过程。 这会给网络训练带来困难。  

深度图像先验的出现为无监督深度相位检索方法的发展提供了新的思路。 [1]中提出的深度相位解码器算法，受到使用未经训练的生成dnn作为图像先验模型的思想启发，通过最小化测量强度图像与深度解码器网络生成的假设图像之间的欧氏距离来重构相位。 类似地，Wang等人[26]提出用未经训练的神经网络恢复相位，其参数是通过最小化测量强度与通过成像模型从网络输出投影到输入平面的图像之间的损失来获得的。 在这两种方法中，网络结构直接借鉴了一些流行的方法，如[1]中的深度解码器和[26]中的U-Net。 两种方法都声称融合了成像模型，但这只是通过损失函数工作，而不影响网络设计。   

                              

尽管基于深度学习的方法在相位检索问题上表现出良好的性能，但其可解释性和泛化性仍然是一个主要的挑战，仍需要进一步研究。 本文提出了一种有效的、可解释的、无监督的、基于物理的复值深度神经网络用于相位检索。 我们的方法有以下优点：

• 我们的网络设计灵感来自著名的替代投影相位检索算法。 我们将替代投影方法的迭代过程展开为前馈神经网络，其层模拟处理流程。 这使得我们的网络易于理解和理解。  
• 成像过程的物理模型嵌入到神经网络结构和损失函数中。 后者使网络训练不需要任何标记数据。 与[26]相比，我们的双物理嵌入策略使网络推理更容易，因此需要的网络参数更少。  
• 提出了一个复值U-Net，用于在目标和图像平面更新中隐式定义图像先验，而不需要额外的硬件设备或原始GS算法及其变体所做的多次测量。  据我们所知，该方法是文献中第一个利用复值神经网络和双物理嵌入策略来解决相位检索问题的方法。 我们的方法在实际的相位检索应用于无透镜显微成像方面取得了优越的性能。  

 2、预热

在本节中，我们将首先介绍无透镜显微镜成像的成像物理，然后通过替代投影重温经典的相位检索(PR)，这激发了我们用于相位检索的深度展开神经网络。  

2.1、无透镜显微成像物理机理

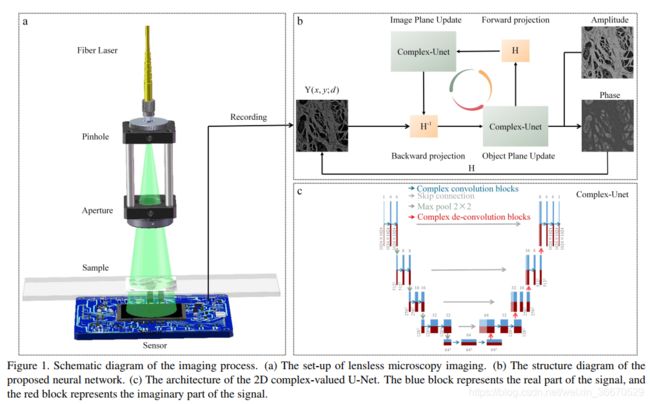
无透镜显微成像系统如图1 (a)所示。 定义作为准单色波照射下的生物样本。 距生物样品d距离处的光场可以表示为：

             

式中为离散傅里叶变换，为其反变换; ⊙表示矩阵中相应元素的积; 为频域坐标。 为角谱表示定义的传输矩阵：

           

式中I为虚单位; D为样品到摄像机的距离; λ是光的波长; K是波数。 相机接收到的是强度信息，根据振幅建立光场之间的传播方程，相机捕捉到的图像可以表示为  

         

式中，为强度测量值。 重构后的光场可通过求解以下优化问题进行估计  

            

在推导复值时，确定相位图像为其参数。  

2.2、PR的经典交替投影方法  

文献中最著名的PR方法是alternative projection algorithm，由Gerchberg和Saxton提出，后来由Fienup推广。 接下来，我们简要介绍了交替投影法的过程。 如图2所示，它从一个随机初始估计开始，然后迭代执行以下步骤。 例如，在第k次迭代中:

•投影。 使用角谱表示将信号投影到图像平面：

            

•图像平面更新。 一般认为图像传感器记录的强度就是像面光场的真实强度。 因此，捕获的强度用来代替投影到像平面上的：

             

其中angle(·)表示计算相位的运算。  

 •反向投影。 图像平面上的信号更新后，变得更接近实际传输到图像传感器的光场的真值。 然后将更新后的信号投影到目标平面上：

                 

式中H−1(·)表示H(·)的反变换，由于光的传播是可逆的，所以在(2)中设置d =−d进行。  

 •目标平面更新。 最后，利用先验知识在目标平面上对信号进行更新，使其更接近地面真实。 文献中提出了多种获取目标平面先验的策略。 这是各种迭代投影方法之间的主要区别。 例如，Gerchberg-Saxton (GS)算法[6]需要知道物体平面的振幅，这是由一个额外的显微镜捕获的; Zheng et al.[29]等人提出的傅里叶ptychographic microscopy (FPM)采用LED阵列获取多角度图像作为光谱先验; 另一种常用的目标先验方法是采用不同离焦距离的多个观测平面[18,7]，这被称为多距离相位检索(MDPR)。 这里我们以GS算法为例，其中目标平面更新表示为： 

           

其中表示另一台显微镜捕捉到的物面振幅。

反复执行上述过程，直到达到停止条件。 最后得到恢复后的复信号，包括振幅和相位信息。 由以上描述可以发现，在基于可选投影的相位检索中，目标平面更新步骤起着至关重要的作用，而目标平面先验的定义是其中的核心。 尽管基于投影的替代PR算法在实际应用中运行良好，但这需要额外的硬件设备来获得可靠的约束条件，如[6,29]中的另一个显微镜或LED阵列。    

 3、提出的方法

在这项工作中，我们试图将迭代过程展开为一个前馈神经网络，其层模拟基于替代投影的PR方法的处理流程，而不引入额外的硬件或多个测量。 为了实现这一目标，需要仔细考虑三个主要问题:1)现有的基于DNN的方法通过直接将观测振幅映射到理想的相位来解决PR问题，其中忽略了成像过程的物理特征。 2)成像模型涉及到傅里叶变换，产生复数，传统的实值深度网络不再适用。 3)目前基于深度学习的PR方法依赖于监督学习，有大量的训练实例。 然而，对于许多实际的光学成像场景，地面真相是未知的，因此不可能收集对数据进行端到端学习。

为了应对上述挑战，我们提出了一种复杂加权深度神经网络，用于展开迭代投影进行相位检索，将图像先验和成像物理封装到网络设计中。 我们的方法以一种无监督的方式工作，通过将成像物理纳入损失函数，将网络的权值与捕获的强度测量值拟合，从而重建所寻求的相位。 与PR的经典迭代投影相对应，该神经网络由向后投影、目标平面更新、正向投影和图像平面更新四个模块组成。 在一次迭代中进行两次后向投影和目标平面的更新。 下面，我们将首先介绍由复值神经网络表示的成像模型，然后详细阐述这四个模块。  

3、提出的方法

在这项工作中，我们试图将迭代过程展开为一个前馈神经网络，其层模拟基于替代投影的PR方法的处理流程，而不引入额外的硬件或多个测量。 为了实现这一目标，需要仔细考虑三个主要问题:1)现有的基于DNN的方法通过直接将观测振幅映射到理想的相位来解决PR问题，其中忽略了成像过程的物理特征。 2)成像模型涉及到傅里叶变换，产生复数，传统的实值深度网络不再适用。 3)目前基于深度学习的PR方法依赖于监督学习，有大量的训练实例。 然而，对于许多实际的光学成像场景，地面真相是未知的，因此不可能收集对数据进行端到端学习。  

为了应对上述挑战，我们提出了一种复杂加权深度神经网络，用于展开迭代投影进行相位检索，将图像先验和成像物理封装到网络设计中。 我们的方法以一种无监督的方式工作，通过将成像物理纳入损失函数，将网络的权值与捕获的强度测量值拟合，从而重建所寻求的相位。 与PR的经典迭代投影相对应，该神经网络由向后投影、目标平面更新、正向投影和图像平面更新四个模块组成。 在一次迭代中进行两次后向投影和目标平面的更新。 下面，我们将首先介绍由复值神经网络表示的成像模型，然后详细阐述这四个模块。  

3.1、二维复杂值U-Net

在该方法中，我们旨在结合基于模型的备选投影方法和深度神经网络的优点，从而同时实现网络的可解释性和推理有效性。 在迭代投影法中，成像物理知识被显式地嵌入到投影约束中。 但是，如第2节所述，由于涉及到复杂的运算，使得常用的实值神经网络不适用。 我们建议使用复值神经网络来实现我们的目的，并将众所周知的实值U-Net扩展到用于2D图像的复值版本。  

如图1 (c)所示，复值U-Net (CVU-Net)与实值U-Net具有相同的结构，由四个主要组成部分组成: 卷积块(3 × 3复卷积，复批归一化，复漏ReLU)，最大池化块(2 × 2)，上卷积块(上采样，3 × 3复卷积，复批归一化，复漏ReLU)和跳跃连接块。  

在下面，我们定义这些复值构建块。 给定一个复值卷积滤波器，其中和是两个实值矩阵，对一个复输入h和F的复卷积运算可以通过  

            

复卷积可以通过共享权的两种不同实值卷积操作来实现。 在实值神经网络中，ReLU应用广泛。 然而，对于一个复信号，其实部或虚部通常是负的。 因此，我们建议利用复杂的泄漏的ReLU。 此外，对于复值激活函数，证明了实部和虚部的分离可以为一些任务带来好处。 因此，在我们的方案中，复杂的泄漏的ReLU被实现为  

                

式中为激活层的输入信号; LeReLU(·)是泄漏的ReLU操作符。 对于复值批标准化，类似于复激活函数，我们分别对实部和虚部进行实值批标准化。  

 3.2、深度展开神经网络

接下来，我们将详细介绍所提出的方法，将备选投影方法的推理过程展现为类似于神经网络的分层结构。 得到的公式将深度网络的表达能力与基于模型的方法的内部结构相结合，允许在固定数量的四层单元中执行推理，这些单元可以得到最佳性能的优化。 具体来说，我们的备选投影网络从图像平面开始，设置，几个六层单元逐步执行。 在第k单元中，它包含以下6个层：

•向后投影层：这一层的输入信号是估计图像平面的最后一个单位。 在这一层中，我们使用角谱表示将其投射到物体平面上。 输出信号可以通过:  

              

式中Re(·)表示求复值信号的实部; Im(·)表示求复值信号的虚部。 和是的实部和虚部。值得注意的是，这一层的信号是真正基于物理的成像过程，不涉及卷积运算。 但它仍然参与反向传播，更新其他层的网络参数。  

•目标平面更新层：这一层的目的是更新对根据估计O(k)(x, y; 0)向后投影层计算。 这实际上是一个信号恢复的问题。 我们没有明确地使用额外的硬件、多平面测量或手工制作的启发式来定义之前的方法，而是通过3.1节中开发的CVU-Net以一种基于学习的方式隐式地进行:  

                     

其中θ为网络参数。 这意味着网络本身就是一个先验模型。  

 •正向投影层：这一层的输入信号为更新后的估计在物平面上，用角谱表示将物平面进一步投影回像平面。 该层的输出定义为：

                        

与反向投影层类似，该层不进行任何卷积运算，只是参与反向传播中梯度的计算。  

 •图像平面更新层：这一层的输入是更新后的估计。与对象平面更新层相似，该层的更新过程可以表述为一个信号恢复问题，由提出的CVU-Net解决：

                 

其中φ为网络参数。 后两层与前两层相同，网络整体框架如图1 (b)所示。  

 Loss function：为了训练所提出的深度展开复值神经网络，考虑到在无透镜显微镜成像中收集密集训练数据的困难，我们不再采用常用的端到端训练方式直接将给定的强度测量值映射到相位。 相反，我们建议将基于物理的公式指定为一个未经训练的深度神经网络，其权重被强制适应给定的强度测量。 具体来说，我们通过角谱表示将网络输出传输回目标平面，并利用其强度值的差异形成损失函数。 我们将损失函数定义为:  

             

其中表示我们提出的网络，为网络参数。 由于ground-truth阶段不涉及损失函数，我们的方法以无监督的学习方式工作。  

3.3、实现细节

神经网络是在Pytorch 1.7.0平台上使用python 3.8实现的。 我们采用学习率为0.01的Adam优化器[12]来优化网络中的权值。 并在每个优化步骤中对固定输入I添加0 ~ 0.03的均匀分布噪声，以达到更好的收敛性。 在我们的网络中，图像大小设置为1024，图像传感器大小设置为1.34µm。 迭代次数为200次。 我们使用的计算机是CPU E5-2620 V4, 64GB RAM, NVIDIA GTX 1080TI。  

4、实验

在本节中，我们提供真实成像任务的实验结果-无透镜显微镜成像-以证明我们的方法的有效性。 在下面，我们首先介绍实验设置，然后比较提出的模型和最先进的算法，最后提供烧蚀分析。

4.1、实验设置和数据集

 为了验证所提出算法的性能，我们搭建了一个典型的无透镜显微镜，如图1 (a)所示。为了增加器件的数值孔径(NA)，我们去掉了相机的包装，以减少样品和图像传感器之间的距离。 光纤激光器发射出发散的球面波，通过准直透镜将其转化为平行光。 接收装置是一个CMOS传感器(Sony, IMX206, 1.34µm×1.34µm)，在532nm激光波长下，置于精密线性台上。  

 4.2、和SOTA的比较

由于本文提出的网络是无监督的，为了公平比较，我们引入了三种具有代表性的无监督的比较研究方法:  

•支持约束[17]的GS算法。 GS算法是相位恢复算法的起源，本文的迭代投影策略是受此工作的启发。  

•Zhang等人提出的基于压缩感知的方法[28]。 在深度学习出现之前，压缩感知是解决工程优化问题的有用工具。  

•Wang等人提出的基于深度学习的无监督方法PhyseNet。[26]。 由于PhyseNet只能处理纯相样品，为了公平比较，我们用一个复杂的U-net代替了他们框架中使用的U-net。 虽然我们的网络有3个复杂的u网，但是由于我们的u网的信道数只有PhyseNet的1/4，所以总的参数量要比PhyseNet少。 

    

              

实验结果如图4所示。 (k)为收集到的衍射图样，(a)， (b)为地面真值，通过收集8×5×5体积数据计算得到。 (c)和(d)是支持约束为[17]的GS算法的结果。 (c)是振幅结果，类似于地面真实的草图，缺少很多细节;(d)是相位结果。 与(b)相比，它看起来更像二值化的结果。 (e)和(f)是基于压缩感知算法[28]的结果，(e)是振幅结果，有很多伪影。 (g)和(h)由无监督深度学习方法[26]生成。 (g)是振幅的结果,从放大图像的红盒子,和它看起来像一个去噪的版本(e)和比(e)更清晰。然而,(g)仍然失去了大量的细节与结果(h)阶段时,这有很多过度曝光点。 (i)和(j)是我们方法的结果，振幅结果(i)是这些方法中最好的。 它的分辨率远高于其他方法。 但与采样8×5×5 volume data计算的ground truth (a)相比仍有差距。 与地面真实值相比，支撑方法的相位结果(j)仅略暗。 其他比较结果可以在补充材料中找到。 其他样品也可以观察到类似的可视化结果，如图6所示。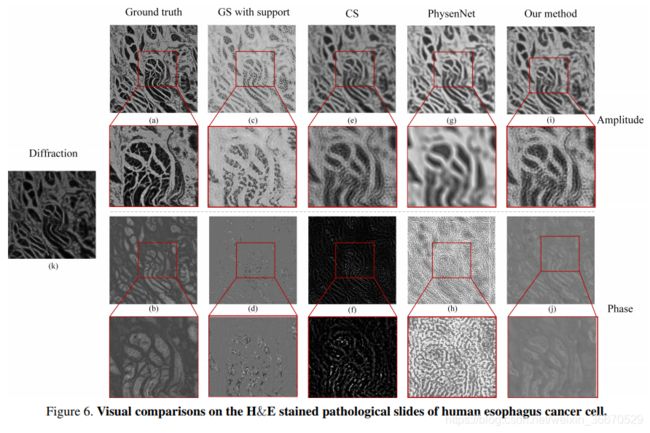        

 4.3、消融研究

在本节中，我们将进行消融研究，以分析所提议框架中每个组件的有效性。 在无透镜成像显微镜系统上，我们报告了三种不同方法的定量和定性结果，其中每一种方法都是逐步添加的:1)只包括基于物理的损失函数; 2)当网络; 3)在网络中加入正向成像模型; 4)将网络展开成可选投影形式。  

 实验如图3所示，(a)为图像传感器捕捉到的衍射图形，(b)为地面真实值，通过收集8×5×5三维体数据计算得到。 使用(c)的方法是我们网络的基本版本，只有基于物理的损耗函数。 (d)的方法是U-net的复数形式。 由(d)可以看出，振幅重建的结果有点像过曝光，有一些类似于水渍的斑点，相位几乎没有恢复。 所使用的(e)算法是基于(d)的。在网络中添加一个基于物理的正向成像模型。 由(e)可以看出，加入正演成像模型后，重构幅值部分得到了明显改善。 但相位结果与真实值仍有很大差距。 所采用的(f)方法是在(e)的基础上，添加后向成像模型，以及相应的物面更新模块和像面更新模块。 可以看出，加入后向成像模型后，反演的相位得到了明显的改善。 振幅图像也得到了改善，但对比不明显。 从这些比较结果中，我们可以看到传统算法与深度学习方法相结合的优势。  

 5、结论

本文提出了一种基于物理的无监督复值深度神经网络。 特别地，复杂加权深度神经网络用于展开迭代投影进行相位检索，从而将图像先验和成像物理特性封装到网络设计中。 我们的方法以一种无监督的方式工作，通过将成像物理纳入损失函数，将网络的权值与捕获的强度测量值拟合，从而重建所寻求的相位。 无透镜显微成像实验结果证明了该方法的有效性。