人工神经网络理论、设计及应用_人工神经网络到底能干什么?到底在干什么?...
转的别人的,觉得写的很好,明白了人工神经网络与传统机器学习、深度学习是个什么关系,是否需要特征工程,转的地址是:
http://www.broadview.com.cn/article/419380www.broadview.com.cn1.McCulloch-Pitts 神经元模型
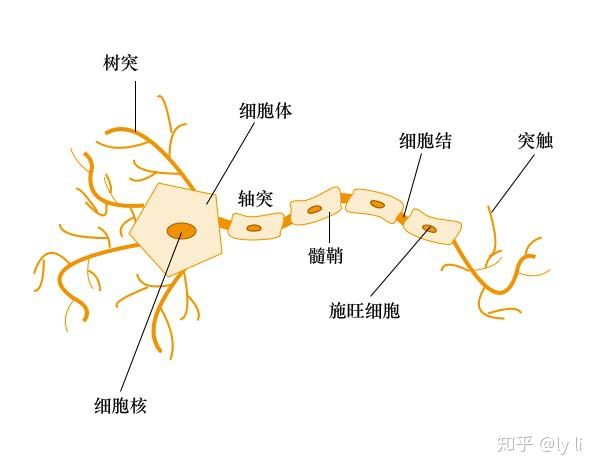
早在1943 年,神经科学家和控制论专家Warren McCulloch 与逻辑学家Walter Pitts就基于数学和阈值逻辑算法创造了一种神经网络计算模型。其中最基本的组成成分是神经元(Neuron)模型,即上述定义中的“简单单元”(Neuron 也可以被称为Unit)。在生物学所定义的神经网络中(如图1所示),每个神经元与其他神经元相连,并且当某个神经元处于兴奋状态时,它就会向其他相连的神经元传输化学物质,这些化学物质会改变与之相连的神经元的电位,当某个神经元的电位超过一个阈值后,此神经元即被激活并开始向其他神经元发送化学物质。Warren McCulloch 和Walter Pitts 将上述生物学中所描述的神经网络抽象为一个简单的线性模型(如图2所示),这就是一直沿用至今的“McCulloch-Pitts 神经元模型”,或简称为“MP 模型”。
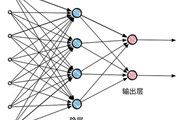
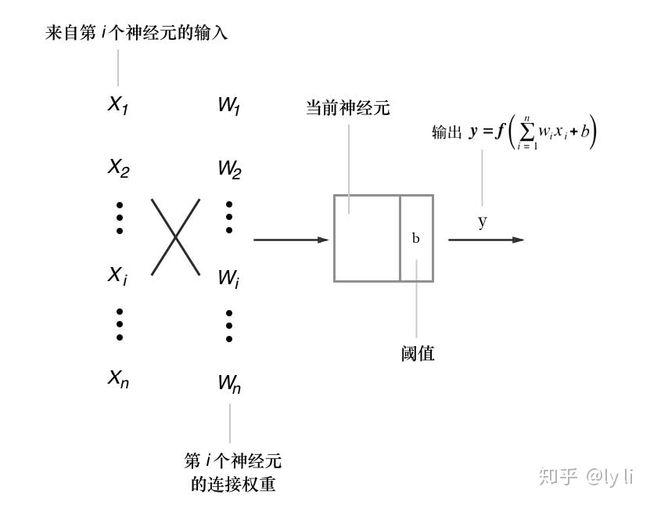
在MP 模型中,某个神经元接收到来自n 个其他神经元传递过来的输入信号(好比生物学中定义的神经元传输的化学物质),这些输入信号通过带权重的连接进行传递,某个神经元接收到的总输入值将与它的阈值进行比较,然后通过“激活函数”(亦称响应函数)处理以产生此神经元的输出。如果把许多个这样的神经元按照一定的层次结构连接起来,就可以得到相对复杂的多层人工神经网络。
生物学所定义的神经网络
McCulloch-Pitts 神经元模型
事实上,从数学建模和计算机科学的角度来看,人工神经网络是认知科学家对生物神经网络所做的一个类比阐释,并不是真正地模拟了生物神经网络。人工神经网络可以被视为一个包含了许多参数的数学模型,而这个数学模型是由若干个函数相互嵌套代入而得到的。
图2 中的神经元可以表示为
其中xi 是来自第i 个神经元的输入,y 是输出;w 是加权参数(连接权重),b 为偏值(Bias)(某些文献中偏值也被称为阈值,为了与Threshold 阈值区分,本书统一使用偏值);f 表示激活函数(Activation function)。有效的人工神经网络学习的架构和算法大多有相应的数学证明作为支撑。
注意,神经元的运算可以用矩阵乘法来实现,x 是维度为[1,n] 的一个横向量,W是维度为[n,1] 的竖向量,b 为一个值,矩阵运算为y = f(x *W + b)。在TensorFlow中,这个神经元的运算就是以矩阵乘法实现的。我们拓展一下,若输出5 个神经元且输入的x 有100 个值,则输出y 有5 个值,W 的维度为[100,5],而b 的维度为[1, 5]。
2.人工神经网络到底能干什么?到底在干什么
经典人工神经网络本质上是解决两大类问题:1)分类(Classification);2)回归(Regression)。当然现在还有图像分割、数据生成等问题,但经典机器学习中已经讨论过,把图像分割归为分类问题,把数据生成归为回归问题。分类是给不同的数据划定分界,如人脸识别,输入x 是人脸照片,输出y 是人的ID 号,这个值是一个整数。回归问题要解决的是数据拟合,如人脸年龄预测,输入x 同样是人脸照片但输出y 是人的年龄,这个值是一个连续浮点数。
需要注意的是,广义上来说,数据可以是有标签(Labeled)或者无标签的(Unlabeled),这对应了经典机器学习中的有监督学习(Supervised Learning)和无监督学习(Unsupervised Learning)。在机器学习中,对于无标签的数据进行分类往往被称作聚类(Clustering)。在实际应用中,垃圾电子邮件自动标注是一个非常经典的分类问题实例,股票涨跌的预期则可看作一个回归问题。在实际应用中,有标签的数据往往比较难以获得(或者是会花比较高的代价才能获取,如人工标记),但是对有标签的数据进行有监督学习相对容易。总而言之,无监督学习相对较难,但是无标签的数据相对容易获取。
在“大数据”支持和电脑硬件(如图形处理器GPU)的计算能力不断提高下,人工神经网络和深度学习在分类和回归问题上都取得了空前的成效。可是我们讨论了众多概念,比如网络、单元、连接、权重、偏值、激活函数,知道了人工神经网络可以解决分类(聚类)和回归问题,但是具体怎么使用人工神经网络呢?
让我们回到这个方程:y = f(x_W +b),以一个最简单的分类问题为例子(聚类和回归问题可以举一反三,请读者自己思考):如果有1 万封已经标记好的电子邮件,每一封邮件只可能被标记为垃圾邮件(SPAM)或者非垃圾邮件(HAM),即输出y = 0或者y = 1,换句话说,这是一个二元分类问题。我们的输入xi 和经典机器学习中定义的并无差别,可以是从具体每封电子邮件中提取的关键字,或者是提取的其他特征量。我们往往通过对数据的特征提取和预处理(例如归一化与标准化)构建统一格式的特征向量作为输入。值得注意的是,在现有的很多深度学习算法中,特征提取往往被直接融合到了模型训练过程中,并不会单独实现(但是数据的归一化与标准化往往不可或缺,甚至会最终决定深度学习模型的成败)。在给定预设好的激活函数(Activationfunction)和偏值(Bias)的情况下,我们有了一个训练集(xi,yi),比如第158 号邮件有“on sale”、“省钱”等字眼并且被标记为垃圾邮件,我们通过前向传播和初始化的加权参数由xi 得到y′i,并且和真实的yi 进行比较,然后通过反向传播对加权参数进行更新。我们实际上最终需要学习到的是一组最优的“加权参数”。当一封新的邮件,比如第1 万零1 封邮件被输入的时候,通过已经获取的最优的“加权参数”,就可以自动判别其属于垃圾邮件或非垃圾邮件。当我们有一个很复杂结构的深层网络的时候,同样的原理也可以适用,只不过每一层的网络的输出被当作了下一层网络的输入。
另外,值得深思的是,真实人类的大脑(生物学上的神经网络)是这么工作的吗?
我们注意到人工神经网络的工作往往需要大量的训练数据,而且往往需要大量相对平衡的数据,比如我们需要人工神经网络去识别“猫”和“狗”的图片,我们需要大量的有标记的数据,而且最好是同时分别有大量的“猫”和“狗”的图片,而不是其中一样占绝大多数。这和人类的认知和识别过程是具有天壤之别的,当一个幼儿识别“猫”和“狗”的图片时,往往只需要很少的训练图片,幼儿就可以完成准确率比较高的识别。另外给幼儿看相对较多的“猫”的图片后,往往其对仅有的“狗”的特征也会有很深刻的理解,进而准确识别。这将是未来人工神经网络或深度学习研究人员应该深入去理解的方向,即如何使用有限的少量数据和大量无标记的数据得到准确、有效、稳定的分类和回归预测。
3 什么是激活函数?什么是偏值
通过上述学习,我们理解了基本的人工神经网络架构,但是还有两个概念需要进一步说明:激活函数(Activation function)和偏值(Bias)。
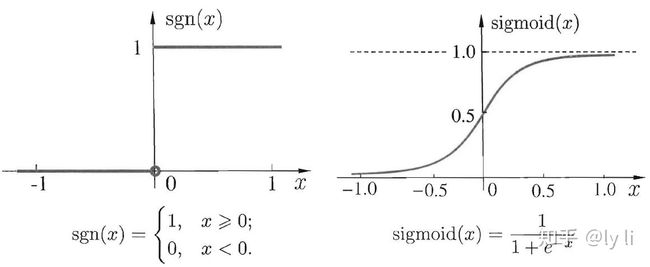
显然,阶跃函数(如图3所示)是理想的激活函数。阶跃函数将输入值映射为输出“0”或者“1”,其中“0”对应于神经元抑制,“1”对应于神经元兴奋。然而,在实际应用中,阶跃函数是不连续且不光滑的。因此,实际常用逻辑函数(Sigmoid 函数)作为激活函数。典型的Sigmoid 函数如图2.3 所示,它把可能在较大范围内变化的输入值挤压到(0,1)的输出值范围内,因此有时也称为“挤压函数”(可以把此激活函数的作用想象为:将线性的输入“挤压”入一个拥有良好特性的非线性方程)。
为什么要非线性?简而言之,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样人工神经网络就可以应用到众多的非线性模型中,使得其表现力更加丰富。
阶跃函数;右图:Sigmoid 函数
那什么是偏值呢?具体来说,偏值控制了激活函数的“左向平移”和“右向平移”。
比如对于标准的Sigmoid 函数(如图2.3 所示),仅在输入x≥0 的情况下才输出1 > y≥0.5,在输入x < 0 的情况下才输出0.5 > y > 0。而若我们想要实现在输入x ≥1 的情况下输出1 > y ≥0.5,在输入x < 1 的情况下输出0.5 > y > 0,这时无论怎样去改变加权参数,都只能改变Sigmoid 函数的形状(或者说是陡峭程度),拐点始终在x = 0,无法满足训练集的要求。但是当加上偏值后,整个Sigmoid 函数就可以被左右平移,问题就迎刃而解了。
注意,现在主流的激活函数是ReLU 而不是Sigmoid,假设函数为y = f(x),则当x <= 0 时y 为0;当x > 0 时y = x。Sigmoid 函数的缺点是在反向传播(Backpropagation)训练网络时,由于在输出接近0 或1 时斜率极小,所以当网络很深时,在反向传播过程中输出层的损失误差很难向输入层方向传递,导致接近输入层的参数很难被更新,大大影响效果,我们称之为梯度弥散(Gradient Vanish)问题。而ReLU 函数解决了这个问题,首先当x > 0,y 是线性的,所以斜率恒为1,不会因为网络深度而出现梯度弥散问题。另外,实践中发现,当x <= 0 时y 为0,可以让神经元具有“选择”特征的能力,这有点像Step 函数。
此外常用的函数还有Tanh、Leaky ReLU 等。Tanh 函数和Sigmoid 函数类似,不过输出范围变成了(-1, 1);Leaky ReLU 是为了解决ReLU 不能输出负数而设计的,可以让训练更加稳定。