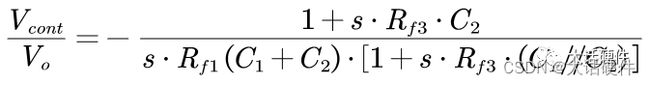开关电源环路稳定性分析（07）——电压型补偿网络

大家好，这里是大话硬件。

在前面的文章中，已经分析了控制级和功率级的传递函数，这一节咱们来分析反馈级的传递函数。

在分析反馈网络的传递函数之前，我想，应该有几个问题需要做一下介绍。

1. 功率级和控制级传递函数说明了什么？

根据前面的传递函数的表达式可知，带有两个阻抗L，C元件的传递函数，在转折频率以后，在增益上斜率为-2，表现为-40dB/dec的特性，在足够宽的频率范围内相位偏移达到-180°。

这样的性质说明两个特点：

（1）传递函数会以较快的频率（-2斜率）穿过0dB；

（2）相位会到达-180

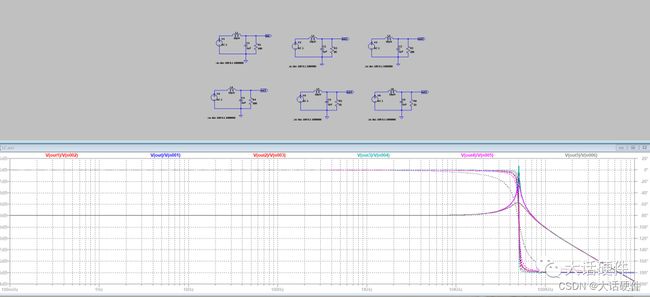
下面仿真的不同负载电阻条件下，LCR 电路的波特图，从结果可以看出，只要是LC的值确定，转折频率确定，谐振峰的大小和负载电阻有关系。在转折频率处相位会有突变，增益会以-40dB/dec的特性降低。

2.零点和极点的作用

左边平面零点会使增益以+20dB的斜率上升，相位增加90度。

左边平面的极点会使增益以-20dB斜率下降，相位减少90°

3. 什么样的开关电源是稳定可靠的？

讲了这么久，我们一直在说开关电源要稳定，到底什么样的电源才算是稳定的呢？

在此之前其实也给大家分析过，判断一个电源稳定与否，除了测试，我们就只能使用数学的工具来判断是否稳定。

因此，在评定开关电源稳定性时，会用下面这两个条件来评定开关电源是否稳定。

增益裕度：GM一般需6dB的增益裕量；

相位裕度：PM一般需要45°的相位裕量；

斜率要求：为防止-40dB/dec增益斜率，相位变化太快，增益曲线穿过0dB的时候，最好是以-20dB/dec；

从上面3个条件可以看出，增益有要求，斜率有要求，相位也有要求。

上面的要求，是不是有点像大家看到的找对象要求：身高>180，体重<150，一般这两条很难满意，往往会再加上几条。

开关电源也是这样，其实增益裕度和相位裕度已经可以保证电源稳定，但是环境中存在的不确定性太多，增加的条件越多，开关电源就越稳定。

4. 开关电源环路补偿其实不算难

分析到这里，其实环路补偿这件事，说难，也不难，说简单也很难。

简单的原因：

首先，我知道判断一个电源是否稳定的要求是什么，上面列出了3条；

其次，我求出了控制级和功率级的传递函数，剩下就是用补偿环路补偿一下；

最后，使整个环路保持稳定，满足要求。

说难的原因：

开关电源的拓扑种类众多，补偿环路形式多样；

开关电源是模拟和数字的混合电路，不同需求，环路补偿要求不一样；

目前没有通用的设计，设计需要差异化；

像不像还在找对象的你，说难吧，你就是需要认识一个异性而已；说不难吧，要认识自己满意的，是不是对你来说，又有些难.

5.电压型和电流型补偿网络

上面通过实际的分析和拆解，把电源环路分析这件事看成是实际和标准之间的差异，是不是简单很多。

目前用的比较多的环路补偿主要有电压型和电流型两种，其中电压型有3种，分为I型，II型，III型，电流的也有3种和电压的基本一致。

电压型补偿拓扑如下：

电流型补偿拓扑如下：

6. 三种类型电压补偿网络介绍

在往下继续读之前，我想你肯定在很多场合听过电压补偿有3型，分别是I型，II型，III型。下面我们对3个类型进行详细分析。

I型

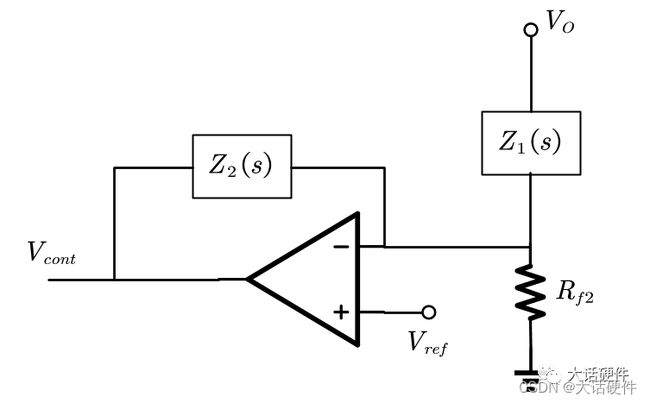
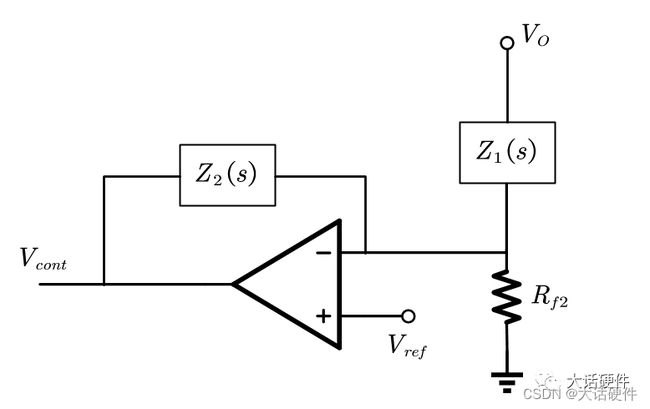
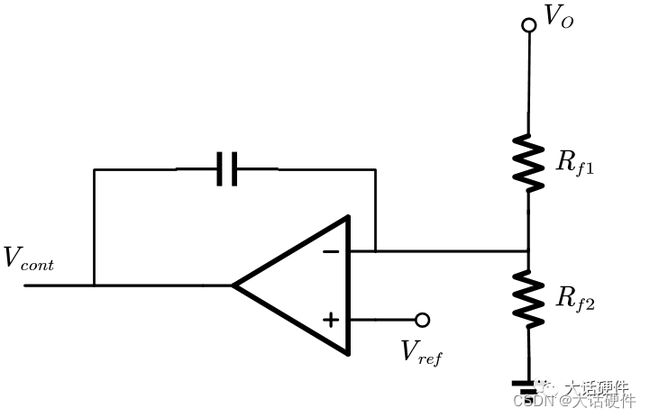
下面这个拓扑就是I型，推导它的传递函数

在推导传递函数时，需要区分直流和交流分析，直流分析的时候，反相端电压是Vref，但是进行交流分析的时候，直流电压等效为0，这个位置我在刚学习的时候，也有些困惑，需要重点理解一下。

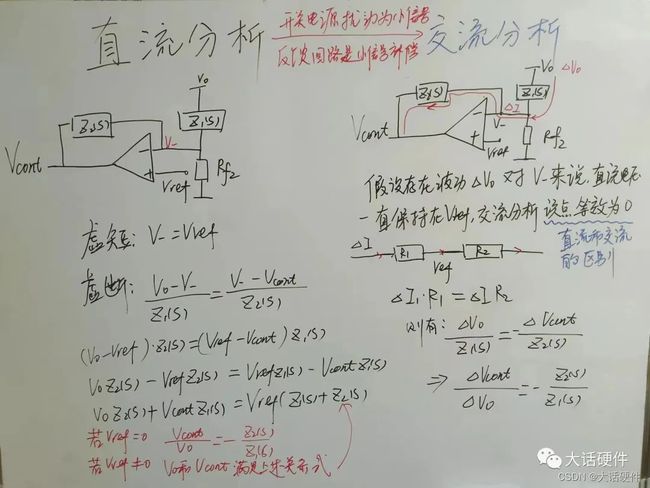
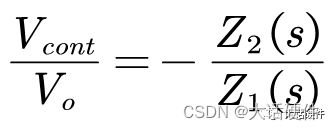
所以I型的传递函数为：

在实际使用的时候，I型的补偿网络在Z2的位置会放置电容，在Z1的位置会放置电阻。

根据零极点的定义，可知I型补偿网络提供了一个零极点，穿越频率为：

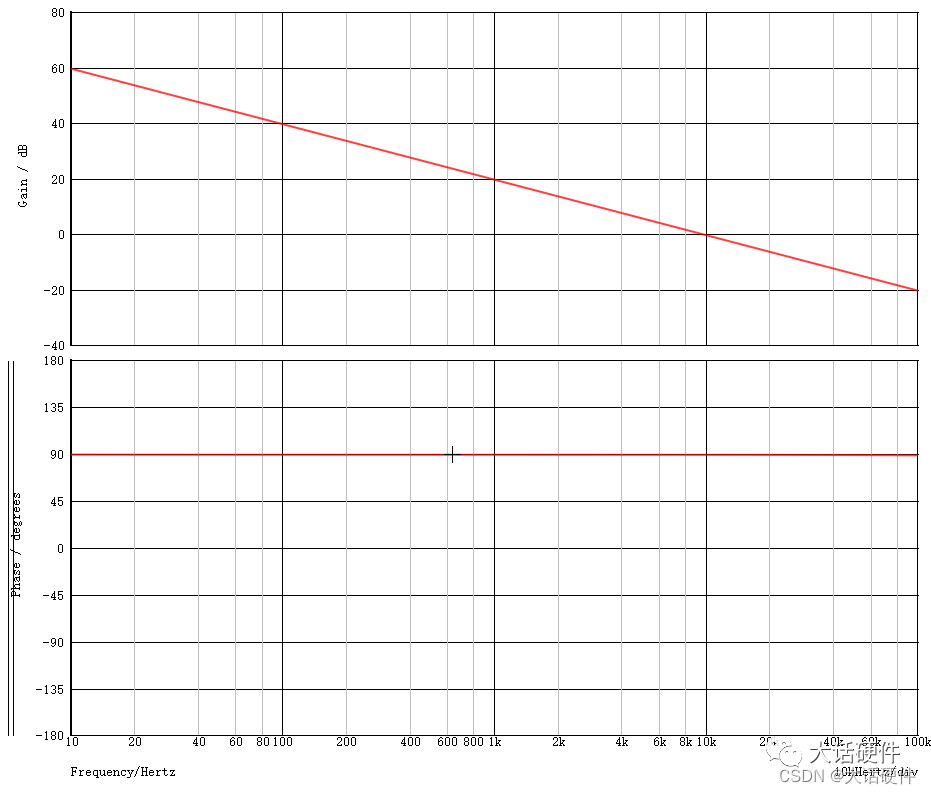
在穿越频率处提供了-90°的相位，增益以-1的斜率穿过0dB

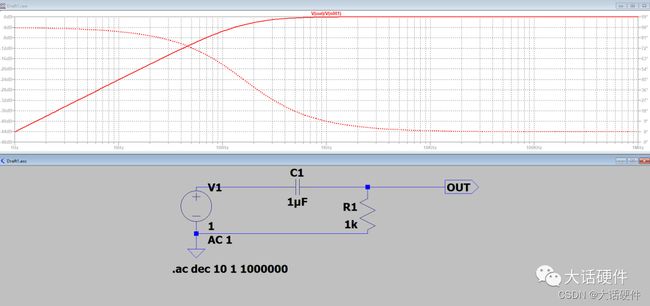
上述仿真的现象和理想中零极点不一样，考虑是LTspice器件模型非理想，换软件仿真

零极点在穿越0dB的时候，斜率-1，相位-90°，这个看起来更符合零极点的波特图。

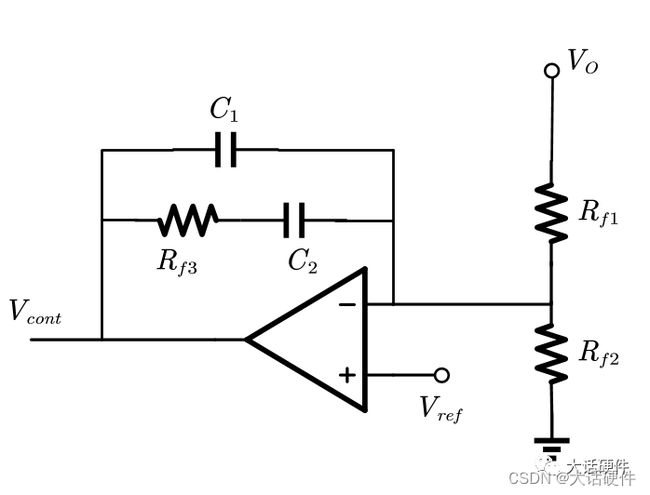
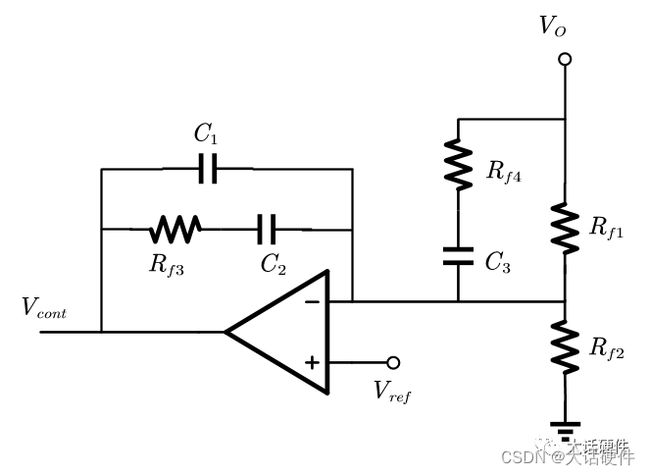
II型补偿网络

传递函数：

可见II型的补偿网络提供了一个零点，一个零极点，一个极点。

III型补偿网络

可见III型的补偿网络提供了两个零点，一个零极点，两个极点。

以上就是电压型不同类型的传递函数，下一节分析电流型补偿网络的传递函数。

目前这些内容在一起可能会让大家有些不知所措，不要担心，后面会把前面所有的内容串联起来，总结出一套环路补偿的步骤供大家使用。