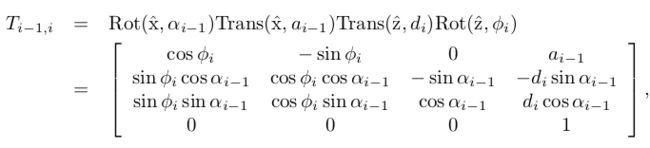【现代机器人学】学习笔记三：前向运动学（Forward Kinematics）
这节的内容比较简单，主要配合习题来看。
在掌握方法以后，对常规的有许多移动副或转动副结构组成的机械臂，计算正向运动学则非常简单。
齐次变换法：
这种方法的特点是，只研究当前关节和上一个关节的旋转平移，然后用下标相乘原则把它合起来。
这个内容在具体实现上，其实可以再扩展为： T = T01*R01*T12*R12*T23*R23*T34
那么上面的T01，就是前一章中所讲的，在1关节的转角为0度的时候，从base系到1关节系，直接裸写得到的旋转和平移矩阵。（参见刚体运动这节【现代机器人学】学习笔记二：刚体运动_zkk9527的博客-CSDN博客，1关节系在base系下的表示）相当于从0系，移动到了1系。然后这时到达了1系，就可以沿1系的转轴进行旋转了，那么这就属于在body系下进行旋转，所以进行右乘。绕哪个轴转，就写出对应的旋转矩阵。其他同理。
旋量指数积法：
相对于基坐标系的螺旋轴：
一个重要前提：近的关节运动会带动远的关节运动。所以要从远及近运动。
相对于基坐标系算末端，假设末端初始为M，那么根据上述前提，就需要从靠近末端的关节开始转。这时这个旋转关节就相当于space系，末端相当于body系，既然是在space系下进行旋转，那么就是左乘。所以就是最终结果就是：
![T(\theta)=e^{[\mathcal{S}_1]\theta_1}e^{[\mathcal{S}_2]\theta_2}..e^{[\mathcal{S}_n]\theta_n}M](http://img.e-com-net.com/image/info8/1bdc89f030b64f558199e0cf29875fe9.gif){kind=small}
那么就看这个中间计算的旋量如何得到的。实际上这里也不是旋量
，它是螺旋轴
。注意实际上
，（注意是
，是延轴的瞬时角速度，而不是指数积上面的角度）而
回顾：
回顾上节：什么是旋量？比如
，那么其中的[w,v]就构成旋量V_s。w就是转轴。
这些容易忘记或记混的东西就要反复，循环的回顾记忆。
回到上面的计算过程：
旋转关节：
1.首先，把机械臂统一都拉到零位，得到末端相对于基坐标系的表示M。
然后盯着space系，根据各个关节轴，看看关节轴在space系下是怎么归一化表示的：例如关节轴转动的那个轴，在space系下是z轴的方向，那么S中的w就是(0,0,1)，其他同理。
2.得到关节轴后，根据
，计算v，这里q是关节转轴上任意一点在基坐标系下的度量。
3.计算得到[w,v]以后，根据螺旋轴的求hat操作：
![[\mathcal{S}]=\begin{pmatrix} [w] &v \\ 0 & 0 \end{pmatrix}](http://img.e-com-net.com/image/info8/8ce4105ad85d4f56b4a7a449323e0c29.gif){kind=small}
然后代入上面的T公式中，
就是这个关节的转角。
移动关节：
1.移动副，则直接代入w就是0。那么v在这里就是关节轴正向的单位向量在基坐标系下的度量， 代表移动的距离。
2.采用上述相同的对螺旋轴求hat的操作，然后代入T公式。
回顾：
在这个公式中，h表示截距（延轴方向的线速度/角速度），但是对移动副而言，没有角速度，所以h会无限大。所以对于移动副，从旋量到螺旋轴的过程，就是
，相当于只对旋量的v进行归一化，那么作用在现在这里，就是关节轴正向的单位向量在基坐标系下的度量。
对于转动副而言，为什么没有后一项了，只剩下前一项？原因也类似，因为转动副没有沿轴方向的线速度。
相对于末端坐标系的螺旋轴：
依据从远及近运动的原则，既然是相对末端系，所以M如果代表space系，1关节此时就代表body系。既然是在body系下旋转，因此就是右乘，所以上面的公式变为：
![T(\theta)=Me^{[\mathcal{B}_1]\theta_1}e^{[\mathcal{B}_2]\theta_2}..e^{[\mathcal{B}_n]\theta_n}](http://img.e-com-net.com/image/info8/fce847af2b1d46f49f8a846f67c4e79a.gif){kind=small}
这里和上面相对于基坐标系的公式相比，看似S变成了B，这里的S和B其实都是螺旋轴，这里之所以叫B，是因为指的是相对末端body坐标系。
计算方法和相对基坐标系的一样，只不过这里确定w和v的时候，都是先拉成机械臂的零位，然后以body系作为参考，从而确定轴的方向。
注意：不管是“相对于基坐标系的螺旋轴”，还是“相对于末端坐标系的螺旋轴”，两种方式计算出来的都是前向运动学的结果，即末端相对于基坐标系的表示。
方法名称中的“相对于基坐标系”或“相对末端坐标系”都是指的是计算中用到的“螺旋轴”是用的哪个坐标系的螺旋轴，可绝对不可以理解为计算出的FK的结果是“相对于基坐标系”（末端相对于base）或“相对于末端坐标系”（base相对于末端）。
FK的结果就是末端相对于base的表示。
插入知识点：
7轴机械臂，额外的第7个关节表示机器人完成末端任务是冗余的，这个额外的自由度可以用于避障或优化某一目标函数，例如满足所需末端位形的前提下功率最小。
PoE方法的好处在于，中间坐标系究竟是怎么样的，可以完全不考虑。爱怎么样就怎么样，只要指定基坐标系和末端坐标系就可以了。
DH表示法
DH表示法是一种传统的表示法，有四个参数：
：连杆长度，就是两个轴之间公垂线的长度。（不一定是真实两杆的长度）
：连杆扭转角，可以理解为，如果沿着上面的 ，把两个连杆相交以后，再沿着公垂线转多少度，就可以使得两个关节轴完全重合。
注意，这两个的下标是i-1，其意味着在推公式，列DH表格的时候，表格的行数从1开始写，并且写的时候，要看从0坐标系出发经过怎么样才能到1坐标系。
连杆偏距
：两轴重合后，沿着轴的方向平移多少，就可以使原点重合。
关节转角
：两轴原点重合后，旧的轴需要旋转多少，就可以和新的轴的角度保持一致。
注意，这两个的下标是i，意味着，在列DH表格的时候，算它俩的时候，上一个轴已经沿着x轴挪到了当前轴上，z轴已经重合了。
如果是移动副，连杆偏距
对于DH参数中，英文字母表示的是距离，希腊字母表示的是夹角。
DH表示法需要事先把所有的关节的坐标系都确定下来。即：先定坐标系，再定DH参数。
1.根据先把所有的z轴都确定。选好基坐标系和末端坐标系，基坐标系尽可能和杆1的连杆坐标重合，末端坐标系尽可能选在末端执行器的某处。
2.再确定x轴，方向是从当前z轴指向下一个z轴。（如果z轴相交或平行，则多种可能性，自己指定一个x轴的朝向即可）
3.根据右手定则，确定y轴。（不过DH法，定不定y轴其实也没啥用）
4.写DH表，确定移动副和转动副的变量。（注意，关节转角是，旧的轴先转某个角度，和新的轴的零位重合了，再加上新的轴可以转的角度。连杆偏距也是同理，不能说这俩就是把新轴的变量塞上去就可以了）
总结：DH就是分为四部：
先沿着公垂线平移（沿x轴平移），再沿着公垂线旋转（沿x轴旋转），再沿z轴平移，再沿z轴旋转。
首先从公垂线开始，公垂线是DH中最重要的参数，所以由它开始，平移完，才开始转。辅助记忆：字母表中a是第一个，所以DH中从a开始。
因为都是沿着操作以后的轴进行下一步操作，所以相关操作一律是右乘：
DH法的优点在于，仅用4个参数就表示了六自由度的内容。这个是因为它设立了特殊的坐标系表示，只沿着x和z平移旋转，而和y无关。
但这也是缺点，需要好好的设置坐标系才可以，搞起来比较麻烦。所以设置坐标系的时候，末端要小心，避免导致DH算不出来，需要沿y轴操作事情发生。。另外DH的缺点是可能存在病态问题，相邻两关节轴平行的时候，一点点误差就会导致公垂线的巨大变化。
书中讲：对开链运动学的FK来说，DH几乎没有实际价值。（晕，那你讲它干什么？？）
不过另一本比较经典的《机器人学导论》中，却只有DH表示法。另外在日常工作中，也经常听到其他同事，包括机械专业、控制专业的同学提到DH表示法，目前我司的机器人的FK貌似就是用的DH算的。。这块不是我负责，改天确认一下。。不同机器人出厂进行参数标定的时候，就是有一些dh参数的标定，不同机器人不太一样。所以我认为这里好像也并不是像书中说的，DH完全没有价值。我个人认为这是流派之争，捧一踩一。。聊天的时候，他们说起来也会说：“他们搞旋量的那帮人....”
POE和DH的关系：
这个因为四项相乘当中，移动副或者转动副，都会有三个是常数项，剩下的那一项也可以用Poe表示一下，最后各个关节都这样表示，化简到最后，就是POE公式。。