多类别逻辑回归简单实现 Python

目的：利用多类别逻辑回归实现手写数字（0-9）的识别

方法：将一对多问题分解成 多个二元问题。

数据：ex3data1.mat

一、读入数据与展示

1.1 读入数据

因为这次是一个mat数据，我们与要引入新的包来读取数据。如下图所示：

import scipy.optimize as opt
from scipy.io import loadmat


data = loadmat('../data/exc_3/ex3data1.mat')
x = data['X']
y = data['y']

1.2 数据展示

fig, ax_array = plt.subplots(nrows=10, ncols=10, sharey=True, sharex=True, figsize=(12, 12))
for r in range(10):
    for c in range(10):
        ax_array[r, c].matshow(np.array(sample_images[10 * r + c].reshape((20, 20))).T,cmap=matplotlib.cm.binary)
        plt.xticks(np.array([]))
        plt.yticks(np.array([])) 

二、 算法实现

2.1 数据处理

我们打印x的形状知道 x 是一个 5000 x 400 的矩阵， 也就是意味着 有 400 个 features 

        1）theta的处理：

        那么意味着theta是一个 401 个。而在本题中，我们利用二分类的方法去实现10个数字的识别。那么将需要10个分类器。也就是说我们可以把 theta定义成一个 10 x 401 的矩阵。

        2）y的处理：

        由于定义成二分类问题，那么我们只需要，利用一个新的变量来存储y的值。循环10次即可。

也就是说：我们在预测数字i的时候，如果时数字i，那么就是1（positive），如果不是数字i，那就是 0 （negative）。这样一来，就化成数字i 和 其他 这样的二分类问题。通过minimize cost function拟合到theta

        3）x的处理：

        由于theta_0 的系数为1，只需在x前加一列 1 即可。

代码如下：

def one_vs_all(X, y, num_labels, learning_rate):
    rows = X.shape[0]
    params = X.shape[1]

    # 定义 num_labels 个 分类器
    all_theta = np.zeros((num_labels, params + 1))

    # 插入一列 1
    X = np.insert(X, 0, values=np.ones(rows), axis=1)

    # 循环10次，注意这里0的的y值为10，所以我们循环1-num_labels+1 也就是1-10
    for i in range(1, num_labels + 1):
        theta = np.zeros(params + 1)  # 初始化 第i个的 theta

        # 初始化output结果。也就是 对于 num_labels 个数据。
        # 也就是说第i个数字的分类器
        # 意思是，我们在预测数字i是，实际上是数字i我们定义为1， 不是数字i 我们定义为0
        # 这样一来，我们就可以通过minimize the cost function来拟合以获取theta，从而获得相应的decision boundaries
        y_i = np.array([1 if label == i else 0 for label in y])
        y_i = np.reshape(y_i, (rows, 1))

        # minimize the objective function
        # fmin = minimize(fun=cost, x0=theta, args=(X, y_i, learning_rate), method='TNC', jac=gradient)
        fmin = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y_i, learning_rate))
        all_theta[i - 1, :] = fmin[0]

    return all_theta

2.2 编写cost和gradient函数

下面我们只需要编写cost函数和gradient函数，然后和之前一样调用高级算法优化函数即可

cost函数：

def cost(theta, x, y, lamda):
    theta = np.matrix(theta)
    x = np.matrix(x)
    y = np.matrix(y)
    # print("the function shapes are: ", x.shape, y.shape, theta.shape)
    term = np.multiply(-y, np.log(sigmoid(x * theta.T))) - np.multiply((1 - y), np.log(1 - sigmoid(x * theta.T)))
    # term2 = np.power(theta.T, 2)
    # 这里如果使用 term2 是将theta_0也带入进去了，但是我们一般不考虑theta_0
    term3 = np.power(theta[:, 1:theta.shape[1]], 2)
    # print("一下是两term的对比")
    # print(term2.shape, type(term2))
    # print(term3.shape, type(term3))
    lamdaTerm = lamda * np.sum(term3) / (2 * len(x))  # 惩罚项
    # print("和的类型为：", np.sum(term3), type(np.sum(term3)))
    return np.sum(term) / len(x) + lamdaTerm

gredient函数：

def gradient(theta, x, y, lamda):
    theta = np.matrix(theta)
    x = np.matrix(x)
    y = np.matrix(y)
    parameters = int(theta.shape[1])
    grad = np.zeros(parameters)
    error = sigmoid(x * theta.T) - y

    # grad = ((x.T * error) / len(x)).T + ((lamda / len(x)) * theta)
    # 这里是否可以写成 (error.T * x) / len(x) +  ((lamda / len(x)) * theta)

    grad = (error.T * x) / len(x) + ((lamda / len(x)) * theta)   # 可以
    # theta_0 不做正则更改
    grad[0, 0] = np.sum(np.multiply(error, x[:, 0])) / len(x)
    return np.array(grad).ravel() 

 最后调用函数，输出一下theta结果如下：

 all_theta = one_vs_all(data['X'], data['y'], 10, 1)
 print('all_theta is:\n', all_theta)

 

 

三、结果分析

        我们编写一个预测结果函数，然后在一个循环内分别整体比较。得到整体准确率。代码如下：

预测函数：

def predict_all(X, all_theta):
    rows = X.shape[0]
    params = X.shape[1]
    num_labels = all_theta.shape[0]

    # 插入一列 1
    X = np.insert(X, 0, values=np.ones(rows), axis=1)

    X = np.matrix(X)
    all_theta = np.matrix(all_theta)  # 将得到的theta用于观测预测结果

    # sigmoid函数
    h = sigmoid(X * all_theta.T)

    # 取10个分类器预测值最大的那个作为我们的预测结果
    h_argmax = np.argmax(h, axis=1)

    # 下标转换
    h_argmax = h_argmax + 1

    return h_argmax

y_pred = predict_all(data['X'], all_theta)
# print("y_pred is ", y_pred)
count = 0
pos = 0
for number in y_pred:
    if number[0] == y[pos][0]:
        count = count + 1
    pos = pos + 1

print(classification_report(data['y'], y_pred))

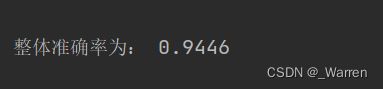
print("整体准确率为：", count/5000)

 输出如下：