PC-GAIN文献总结
目录
一、摘要
二、模型介绍
1、GAIN
2、PC-GAIN
三、实验
1、实验的部分细节说明
2、实验结果对比
3、图像修复
一、摘要
缺少值的数据集在现实世界的应用程序中非常常见。首先介绍一种生成模型GAIN, 是最近提出的一种用于缺失数据的深度生成模型,已经被证明比许多最先进的方法表现得更好。但是GAIN只在生成器中使用重构损耗来最小化非缺失部分的插补误差,忽略了能够反映样本之间关系的潜在类别信息。因此本文提出了一种新的无监督缺失数据的插补方法PC-GAIN,该方法利用潜在的类别信息进一步提高了插补能力。
本文贡献:
1、提出了一种新的条件GAN,利用不完全数据中包含的隐含类别信息进一步提高GAIN的插补质量。仅使用低缺失率数据的子集对于确保伪标签的质量至关重要,并且对模型的性能有重要影响。
2、设计了一种有效的预训练程序,只选取部分低缺失率样本进行插补,从而提高伪标签的质量。
3、设计了辅助分类器和判别器,帮助生成器产生难以区分的插补结果,同时保留更好的类别信息。
4、结果表明,该方法在估计精度和预测精度方面均优于现有方法,尤其是在缺失率较高的情况下。此外,无论类别的实际数量是多少,选择较小的集群数量都可以确保模型在实践中的最佳性能,这一特性使该方法更加灵活。
二、模型介绍
![]() 表示一个不完整数据集。对于每一个
表示一个不完整数据集。对于每一个![]() 都有一个对应的二值掩模向量
都有一个对应的二值掩模向量![]() ,其中如果特征
,其中如果特征![]() 被观察到则
被观察到则![]() ;如果特征
;如果特征![]() 缺失,则
缺失,则![]() 。
。
1、GAIN
首先介绍GAIN,在GAIN中,生成器G将不完整样本x、掩码向量m和噪声源作为输入,输出完整样本,然后鉴别器D尝试分辨哪些是观测到的,哪些是输入的。
GAIN中生成器G的输出可以表示为:
![]() (1)
(1)
其中z是一个d维的噪声,![]() 表示Hadamard product. 所以重建的样本可以表示为
表示Hadamard product. 所以重建的样本可以表示为
![]() (2)
(2)
辨别器D的输出是一个二值向量,可以表示为
![]() (3)
(3)
其中h是一个提示向量,![]() 是掩码向量m的预测。
是掩码向量m的预测。
因此GAIN的目标函数可以表示为
其中![]() 是权重参数,
是权重参数,![]() 是交叉熵损失,
是交叉熵损失,![]() 是一个重建损失:
是一个重建损失:
![]() (5)
(5)
![]() (6)
(6)
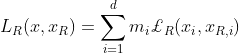 (7)
(7)
而
2、PC-GAIN
众所周知,标签等条件信息可以增强生成器的性能。然而,将现有条件技术应用于常见的插补问题主要面临两个困难。第一,大多数插补问题是完全没有监督的,没有明确的标签可以直接使用。第二,由于数据不完整,特别难以为样本合成合适的伪标签。为解决这些困难提出了基于GAIN的PC-GAIN。
PC-GAIN的流程概括:
1、首先选择低缺失率样本(低缺失率样本中包含的潜在类别信息更可靠)对生成器G和判别器D进行预训练,得到插补数据集。
2、然后,利用聚类算法对插补数据集进行伪标签合成。
3、利用插补数据集和伪标签训练分类器。
4、最后,使用所有的训练数据来训练生成器G和鉴别器D,同时使用预处理的分类器来约束生成器。
下面详细描述PC-GAIN的方法流程:
首先选择低缺失率样本子集:对于任意x,计算它的缺失率r(x):
 (9)
(9)
其中m是数据的掩码向量。
然后根据缺失率做一个升序排序,选择前λN(0 < λ < 1)的样本作为预训练的数据集![]() 。
。
接着根据目标函数(4),用数据集![]() 预训练生成器G和辨别器D可以得到数据集
预训练生成器G和辨别器D可以得到数据集![]() 的插补数据集
的插补数据集![]() ,然后对插补数据集
,然后对插补数据集![]() 应用一种聚类算法合成伪标签
应用一种聚类算法合成伪标签![]() 。(有一点值得指出的是,聚类的类别数量不需要与实际类别的数量一致。作者在实验中发现对于许多UCI数据集,K在4到6之间就足以保证模型的最佳性能。)
。(有一点值得指出的是,聚类的类别数量不需要与实际类别的数量一致。作者在实验中发现对于许多UCI数据集,K在4到6之间就足以保证模型的最佳性能。)
然后用![]() 和对应的伪标签
和对应的伪标签![]() 来训练辅助分类器C。在分类器的帮助下,再次更新生成器G和判别器D。也就是说,要求生成器不仅输出不可区分的输入数据,而且学习不同的类别特征。更具体地说,鉴别器和生成器的目标现在变成
来训练辅助分类器C。在分类器的帮助下,再次更新生成器G和判别器D。也就是说,要求生成器不仅输出不可区分的输入数据,而且学习不同的类别特征。更具体地说,鉴别器和生成器的目标现在变成
 (10)
(10)
其中α和β是超参数,![]() 是一个标准信息熵损失
是一个标准信息熵损失
![]() (11)
(11)
其中![]() 表示辅助分类器的输出。
表示辅助分类器的输出。
以下是PC-GAIN的流程图:
三、实验
1、实验的部分细节说明
由于没有原始数据集包含缺失值,所以本文完全随机地删除部分数据,以形成一个不完整的数据集。同时在实验中采用5次交叉验证,每个实验重复10次,并报告平均性能。
本文对UCI数据的原始插补结果用KMeans++算法聚类,而对于MNIST数据集,使用KMeans++算法对生成器的潜在特征空间进行聚类。
2、实验结果对比
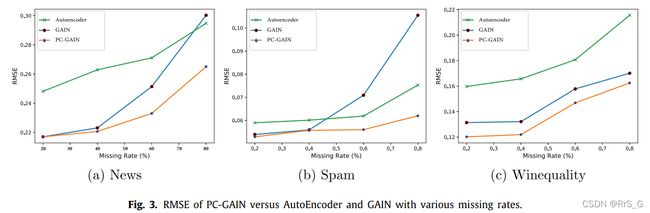
首先在下图中报告PC-GAIN的RMSE和基线模型。可以看出,PC-GAIN除了在WineQuality数据集上比MICE方法略差外,在大多数数据集上性能优于基准测试方法。
接下来以News、Spam和WineQuality为例来说明PC-GAIN在各种缺失情况下的性能。如下图所示,PC-GAIN在各种缺失情况下始终优于比较模型。特别是当缺失率越高时,这种优势就越明显。
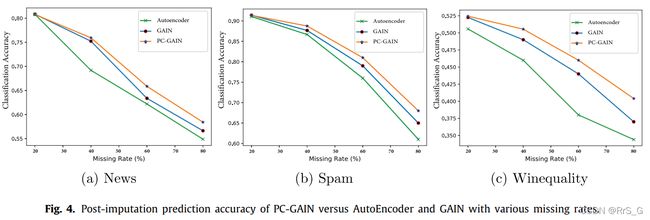
从下图可以看出,PC-GAIN在所有情况下的分类精度都是最好的。此外,随着缺失率的增加,预测精度的提高变得更加显著。这种现象表明PC-GAIN是一种可靠的估算方法,尤其是在高缺失率的情况下。
作者还分别根据λ、β和α的不同的取值以及不同的聚类算法对实验结果的影响做了分析,最终选取最合适的参数值。
3、图像修复
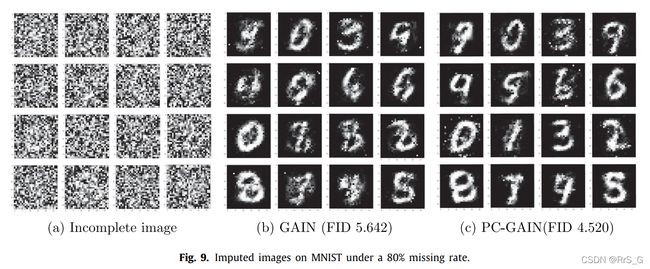
PC-GAIN在图像修复任务中也可以提高GAIN的性能。为此考虑了MNIST数据集。对于MNIST中的每张图像,均匀随机地去除50%和80%像素,使用FID指数比较插补结果。FID表示生成图像的特征向量与真实图像的特征向量之间的距离,较低的FID值通常意味着生成的图像更接近真实图像。
从下图可以看出,PC-GAIN的插补图像比GAIN的插补图像更有凝聚力和流畅性。而且,PC-GAIN的输出在这两种情况下都具有较低的FID值,并且在较高的缺失率时优势更大。