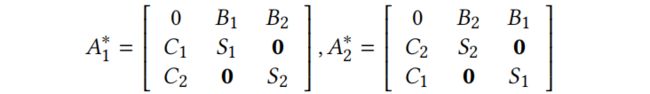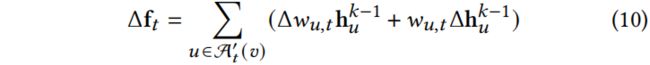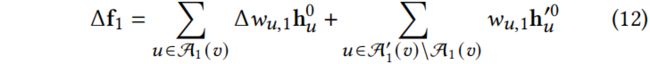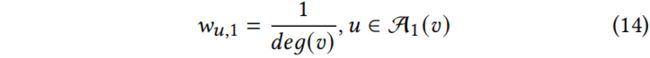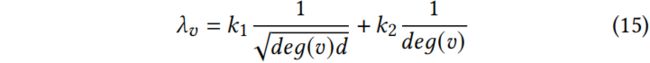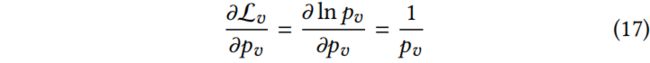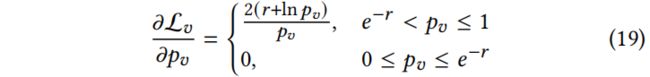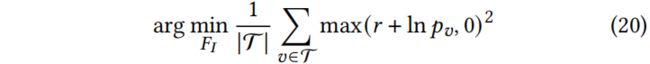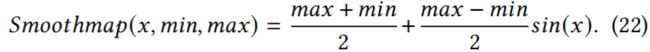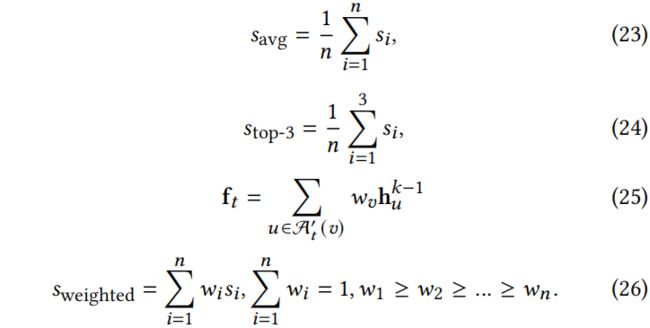KDD2021《TDGIA: Effective Injection Attacks on Graph Neural Networks》论文详解

原文链接：https://arxiv.org/pdf/2106.06663.pdf

evasion attack

1&2 Abstract & Introduction

本文作者分析了图注入攻击（Graph Injection Attack，GIA）设置下的 GNN 网络的拓扑脆弱性（topological vulnerability），在此基础上提出了拓扑缺陷图注入攻击（Topological Defective Graph Injection Attack, TDGIA）以进行有效注入攻击。TDGIA 首先引入了拓扑缺陷边选择策略（topological edge selection strategy）来选择原始节点与注入节点进行连接。 然后设计了平滑特征优化目标（smooth feature optimization objective）来为注入的节点生成特征。

Contributions：研究了 GIA 下 GNNs 的脆弱性，表明 GNNs 作为 non-structural-ignorant models 具有很强的脆弱性，即 GIA-attackable。在此基础上提出了 TDGIA。TDGIA 对应于 GIA 的问题设置由两个模块组成——拓扑缺陷边选择（topological defective edge selection）和注入节点属性生成的平滑对抗优化。具体来说，利用原始图的拓扑漏洞（topological vulnerability）来检测现有的最能帮助攻击的节点，然后以顺序的方式在它们周围注入新的节点。在此基础上，设计了一个平滑损失函数（smooth loss function）来优化节点的特征，以最小化目标 GNN 模型的性能。

3 Problem Definition

本文对 GMA 和 GIA 的问题定义分别如下：

定义属性图，是 N 个节点的邻接矩阵，是节点特征。是预测标签的模型。

GMA 的目标是通过修改原始图 G，最小化在一组目标节点上的正确预测次数：

其中是修改后的图，是节点 i 的真实标签。和是用来衡量修改规模的预定义函数。限制确保了图被对手稍微地修改。

GIA 在保持原图的边和 N 个节点的属性不被修改的同时，直接向图 G 中注入个节点。GIA 用下式构造：

其中是注入节点的邻接矩阵，是表示 G 中节点与注入节点之间边的矩阵，是注入节点的特征矩阵。

GIA 的目标可以形式化为：

其中是注入节点集，受到预算 b 的限制，每个注入节点的度数受到 d 的限制，注入的特征被限制为。这些限制是为了确保 GIA 尽可能不被防御者注意到。

The GIA Process. 首先，训练代理模型；其次，在该模型上进行注入攻击；最后，攻击被转移到一个或多个目标模型。

为处理大规模的数据，GIA 可以按定义分为两步。首先，生成现有节点和注入节点之间的边；其次，优化注入节点的属性。这种分解可以在很大程度上降低复杂性，并使 GIA 适用于大规模图。

目标模型可以是任意的图机器学习模型。

4 GNNs Under Graph Injection Attack

4.1 The Vulnerability of GNNs under Attack

Notes：Permutation Invariant 就是对于原图 G 和 原图的 permutation 图 G’，模型对这两个图的预测是相同的。

一个 GIA-Attackable 的图机器学习模型是一个攻击者可以通过向原图注入节点来改变其对某个节点的预测的模型。根据定义，G1 和 G2 中的节点 i 的索引对于 permutation invariant 模型无关紧要，因为可以应用 permutation 使其在两个图中索引为 0。

根据该定义，大多数 GNNs 是 non-structural-ignorant 的，因为它们依赖于图结构 A 来进行节点分类，而不是仅仅使用节点特征 F。

Notes：如果两个图中的节点拥有相同的标签，但两图的结构是不同的，对两个图上具有相同属性的节点预测相同。也就是与结构无关。

用一个定理来证明 non-structural-ignorant 模型是 GIA-Attackable 的。根据该定理，证明了如果一个 permutation invariant 图是 non-structural-ignorant 的，则它是 GIA-Attackable 的。

Appendix A.3 Proof of Lemma 4.1

假设模型是 non-structural-ignorant 的，则把 G1 和 G2 的公共节点置换到位置 0，则：

考虑一个 GIA 的例子，其中有相同属性的节点以不同的方式注入 G1 和 G2，即，，其中：

假设不是 GIA-Attackable 的，通过定义 2，

但，由于是 permutation invariant 的，即和是经过 permutation 的相同的图，则

这与初始假设矛盾，所以是 GIA-Attackable 的。

Appendix end.

4.2 Topological Vulnerability of GNNs Layers

在节点 v 上执行的 GNN 层可以表示为一个聚合过程：

其中和是向量值函数，表示节点 v 的邻接矩阵，是节点 v 在第 k 层的向量隐式表示。包括直接连接到 v 的节点和可以经一定数量的步骤连接到 v 的节点（也就是节点 v 的邻域节点集）。用来表示节点 v 的 t-hop 邻域，即可以经过 t 步连接到节点 v 的节点。用表示相应的聚合函数。Eq.5 可以进一步表示为： 

Notes：Eq.6 就是把 Eq.5 里的每一步都展开了。

假设通过注入节点扰动图，把变为，通过相对小的量来改变，即。节点 v 在第 k 层的新的 embedding 变为：

Notes：经过注入节点后目标节点 v 第 k 层的隐层表示就是原图中目标节点 v 第 k 层的因曾表示与每个 hop 聚合的变换之和。

把第 k 层的表示为，有

不失一般性，假设具有在 GNNs 中广泛使用的加权平均形式

权重对应于节点 v 在 t-hop 邻域内的拓扑结构。因此，可以利用 GIA 设置下 GNNs 的拓扑漏洞，通过 t-hop 节点注入来构造并扰动的输出。

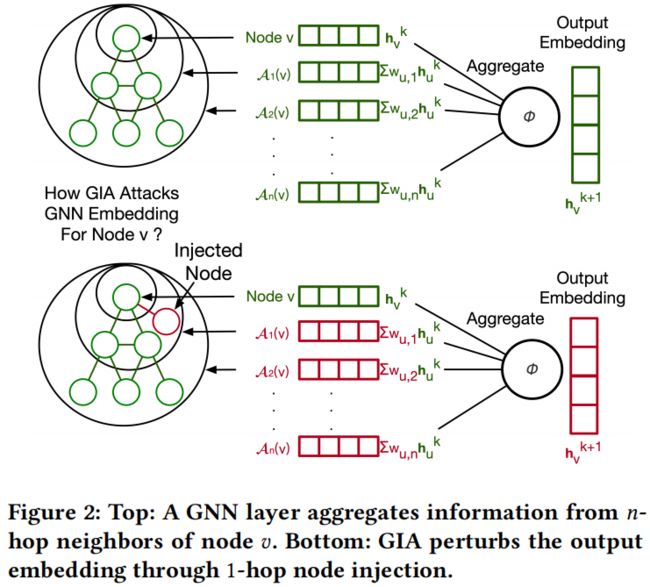
图 2 表示了 1-hop 节点注入的例子。注入的节点可以影响节点 v 的 t-hop 邻域的 embedding，导致在聚合后最终的误分类。现在的问题是如何利用图的拓扑漏洞进行有效的节点注入。

Notes：这里的 topological vulnerability 应该就是可以通过传播在每一个 hop 都增加变化。

5 The TDGIA Framework

TDGIA 的整体流程如图1(b) 所示。

具体来说，TDGIA 包含了与一般 GIA 过程相对应的两个步骤：拓扑缺陷边选择和平滑对抗优化。首先，根据原图的拓扑性质确定重要节点，并依次在其周围注入新的节点；其次，为了最小化节点分类性能，利用平滑损耗函数（smooth loss function）优化注入节点的特征。

5.1 Topological Defective Edge Selection

鉴于 GNN 层的拓扑脆弱性，设计了一种边选择方案，在注入节点和原始节点之间生成缺陷边来攻击 GNNs。

对于节点 v，TDGIA 可以把 k-hop 邻域改变为。对于原来的邻域节点，它们的属性不变。对于注入节点，它们的特征由 0 初始化,。Eq.10 可以发展为：

Notes： 对原图拓扑结构变换和注入节点进行加和，得到 t-hop 聚合的改变量（特征？）。这里的拓扑结构指的是什么？指权重！

从攻击单层 GNN 开始，即 k=1。根据 Eq.8，可以把最大化变为最大化。由于，所以没有改变原来的属性。因此只需最大化

 

在边选择阶段，注入节点的特征尚未确定。因此，策略为首先最大化上的影响并尽可能地扰动。

从 GNNs 常用的开始。继 GCN，使用不同类型的 GNNs

Notes：该公式回答了上面的疑问（拓扑结构是什么）。这里的是指初始注入的节点特征为 0 吗？

而像 GraphSAGE 这样的基于均值池化（mean-pooling）的 GNNs 使用

在 TDGIA 中，当决定注入的节点应该连接到哪个节点时，使用来自 Eq.13 和 Eq.14 的权重组合来衡量节点 v 的拓扑脆弱性。

其中是节点 v 的度数，d 是注入节点度的预算。越大，节点被 GIA 攻击的可能性越大。在 TDGIA 中，通过构造缺陷边将注入的节点连接到具有更高的现有节点。

Notes：边选择方案就是根据来确定目标节点，然后把注入节点连接到目标节点。Eq.15 是选择度数比较小的节点。

5.2 Smooth Adversarial Optimization

一旦选择了注入节点的拓扑缺陷边，下一步就是为注入节点生成特征，以提高攻击效果。给定模型，节点注入后的邻接矩阵，进一步优化注入节点的特征，以（负）影响模型预测。为此，设计了一个带有平滑损失函数的平滑对抗特征优化算法。

Smooth Loss Function. 通常，在对抗性攻击中，反向优化用于训练模型的损失函数。例如，对于目标集中的节点 v，可以使用 KL 散度的逆作为攻击损失

 

其中是正确分类节点 v 的概率。

当趋于 0 时，导数趋于  ，使用这个损失可能会造成梯度爆炸

为了在优化过程中防止这种不稳定的行为，使用平滑损失函数（smooth loss function）

其中 r 是控制因子。因此导数就变成

最后，目标是找到注入节点的最优特征，使所有目标节点的 Eq.18 损失最小：

Smooth Feature Optimization. 在 GIA 设置下，注入节点的特性范围有一个限制。否则，防御者可以根据异常特征轻松地过滤掉注入的节点。在 TDGIA 中，只在优化过程中使用 Clamp 函数来限制特征的范围

但是，这个函数可能会导致 0 梯度。如果一个特征超过了这个范围，它就会被卡在最大值或最小值上。为了平滑 TDGIA 的优化过程，设计了一个 Smoothmap 函数，通过使用下式来平滑地将特征映射到上

5.3 Overall Attack Process of TDGIA

除了拓扑缺陷边选择和平滑对抗优化外，在 TDGIA 中还引入了顺序攻击和使用代理模型。

Sequential Attack. 在 TDGIA 中，采用顺序攻击的思想，批量注入节点。在每一批中，向图中添加少量节点，选择它们的边，并优化它们的特征。重复这个过程，直到用完注入预算。

Surrogate Model. 在黑盒设置下，攻击者没有被攻击模型的信息，因此攻击必须在代理模型上执行。首先在输入图上使用给定的训练数据训练一个代理模型，然后使用生成代理标签。然后对 TDGIA 攻击进行优化，降低对的精度。在选择有缺陷的边时要注意，也使用基于在节点 v 上的 softmax 输出的正确概率作为它的代理标签。然后定义缺陷分数（defective score），如算法1所示。

6 Experiments

6.1 Basic Settings

Datasets. KDD-CUP、ogbn-arxiv、Reddit

Constraints. 注入节点数 b = 500，度数的预算 b = 100。特征限制根据数据集中特征的范围来限制。

在KDD-CUP数据集上进行的实验中，大多数提交的防御方法都包含预处理，对度接近 100 的节点进行过滤。因此，在本实验中，为了避免被过滤掉，采用人为设置的 88 的限制。这些约束同时应用于 TDGIA 和基线攻击方法。

Evaluation Metric. 为了更好地评估 GIA 方法，同时考虑了性能降低和可迁移性。评估主要基于 KDD-CUP 数据集中提出的加权平均精度。该度量根据每个防御模型在 GIA 下的鲁棒性为其赋予一个权重，即越鲁棒的防御得到的权重越大。这鼓励对手专注于所有防御模型的可迁移性，并设计更通用的攻击。除了加权平均精度外，我还提供了所有防御模型的平均精度，以及前3个防御模型的平均精度。三个评价指标如下：

其中是对不同防御模型进行一次 GIA 攻击下降的准确率，即。对于 KDD-CUP，使用给定的数据集，对于 ogbn-arxiv 和 Reddit，以同样的方式设置权重。

最后的实验表明本文方法在多个 GNN 模型上都有较好的攻击效果，用 GCN 作为代理模型能表现出最好的性能。

思考

本文是对大型图的对抗攻击，先通过计算找到目标节点集中最容易进行攻击的节点（具有最高 defective score 的节点），然后把注入的节点连接到目标节点。多个目标节点会与相同的注入节点进行连接。在每次注入节点连接后，在下一次注入节点时，如果有已经连接的节点仍由最高的 defective score，则继续链接。所以每个注入节点连接的节点数目最少是 1，最多是 b。如果 b 个节点都注入完了，还有目标节点没有与注入节点连接呢？此时通过传播就能对其进行改变。具体再看代码。

欢迎讨论和指教。