【HBU】2022秋线上作业-第五次-有关树的判断选择

判断题：

1. 一棵有124个结点的完全二叉树，其叶结点个数是确定的。  √

高度为n的完全二叉树的结点数为2ⁿ-1  124位于64-1~128-1之间，所以这棵树的高度是7，前六层是满的有63个，第7层有124-63=61个   64-61=3    第6层有3/2（向下取整）=1  个  所以整棵树的叶子结点有61+1个

2.二叉树中序线索化后，不存在空指针域。 ×   

非空二叉树中序遍历第一个结点无前驱，最后一个结点无后继，这两个结点的前驱线索和后继线索为空指针

3.对N（≥2）个权值均不相同的字符构造哈夫曼树，则树中任一非叶结点的权值一定不小于下一层任一结点的权值。 √       

非叶子结点权值是下一层结点权值之和

4.哈夫曼编码是一种最优的前缀码。对一个给定的字符集及其字符频率，其哈夫曼编码不一定是唯一的，但是每个字符的哈夫曼码的长度一定是唯一的。  ×     

哈夫曼码的长度不是唯一的

5.对于一个有N个结点、K条边的森林，不能确定它共有几棵树。 ×     

可以确定 有n-k棵

6.树的后根序遍历序列等同于它所对应二叉树的中序遍历序列。   √       

课本推理可得

7.二叉树可以用二叉链表存储，树无法用二叉链表存储。  ×         

树可以转化为二叉树  进而用二叉链表来储存

8.将一棵树转成二叉树，根结点没有左子树。 ×        是没有右孩子啦

9.用邻接矩阵法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关。  √            顶点数有n个的话 就会用一个n*n的邻接矩阵来存图 so和我们的结点个数有关呀

10.用一维数组G[]存储有4个顶点的无向图如下：G[] = { 0, 1, 0, 1, 1, 0, 0, 0, 1, 0 }

则顶点2和顶点0之间是有边的。   √  

邻接矩阵对称 只存下三角就好G[2][0]=1 说明顶点2和顶点0有边

0

10

110

0010

单选题：

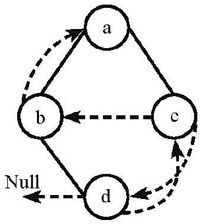
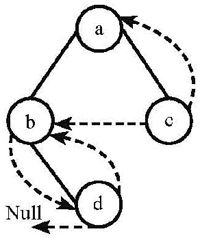
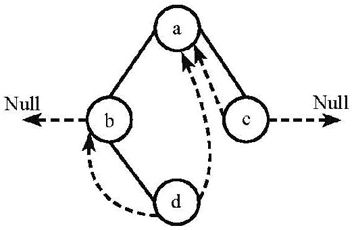
1.下列线索二叉树中（用虚线表示线索），符合后序线索树定义的是：B  后序遍历为dbca

左空指针指向前驱结点  右空指针指向后继结点  只有B符合

A.

B.

C.

D.

2.引人线索二叉树的目的的是（A ）。找一个节点的前驱后继的时候，比非二叉线索树方便快捷

A.加快查找结点的前驱或后继的速度

B.为了能在二叉树中方便地进行插人与侧除

C.为了能方便地找到双亲

D.使二叉树的遍历结果唯一

3.若X是后序线索二叉树中的叶结点，且X存在左兄弟结点Y，则X的右线索指向的是（A）。

 后序是左右中  右线索指向后继结点 BCD均属于左 在X的前面  所以选A

A.X的父结点

B.以Y为根的子树的最左下结点

C.X的左兄弟结点Y

D.以Y为根的子树的最右下结点

4.已知字符集{ a, b, c, d, e, f }，若各字符出现的次数分别为{ 6, 3, 8, 2, 10, 4 }，则对应字符集中各字符的哈夫曼编码可能是： A     建立哈夫曼树 左0右1进行编码

A.00, 1011, 01, 1010, 11, 100

B.00, 100, 110, 000, 0010, 01

C.10, 1011, 11, 0011, 00, 010

D.0011, 10, 11, 0010, 01, 000

5.对 n 个互不相同的符号进行哈夫曼编码。若生成的哈夫曼树共有 115 个结点，则 n 的值是：C

n个叶子结点的哈夫曼树，共2n-1个结点
2n-1=115 解得n=58 

A.56

B.57

C.58

D.60

6.将森林转换为对应的二叉树，若在二叉树中，结点u是结点v的父结点的父结点，则在原来的森林中，u和v可能具有的关系是：B  画画图 3情况是画不出来的

1.父子关系； 2. 兄弟关系； 3. u的父结点与v的父结点是兄弟关系

A.只有2

B.1和2

C.1和3

D.1、2和3

7.对于一个有N个结点、K条边的森林，共有几棵树？A  和判断5可以对应起来

A.N−K

B.N−K+1

C.N−K−1

D.不能确定

8.设森林F中有三棵树，第一、第二、第三棵树的结点个数分别为M1​，M2​和M3​。则与森林F对应的二叉树根结点的右子树上的结点个数是： C

森林转换二叉树是兄弟树相连,再调整，所以除了第一棵树，其他树都在右边，所以是M2+M3

A.M1​

B.M1​+M2​

C.M2​+M3​

D.M3​

由若干个二叉树组成的森林F中，叶结点总个数为N，度为2的结点总个数为M，则该集合中二叉树的个数为：B

设 N0 N1 N2
TNum = NodeNum - EdgeNum
= N0 + N1 + N2 - (N2 * 2 + N1)
= N0 - N2
= N - M;

11.A.M−N

N−M

C.N−M−1

D.无法确定

10.若森林F有15条边、25个结点，则F包含树的个数是：C  N-K；

A.8

B.9

C.10

D.11

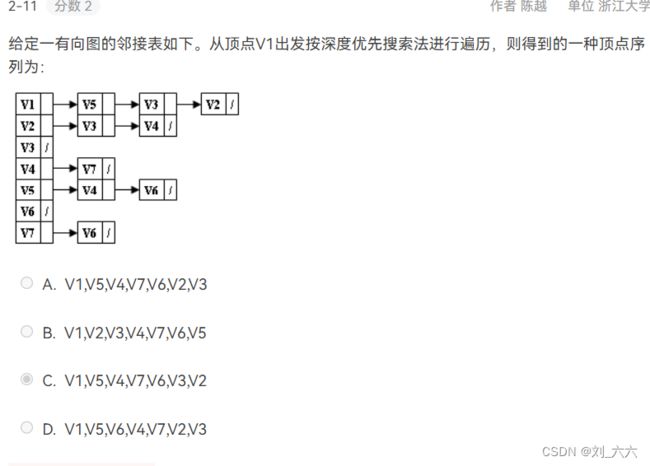
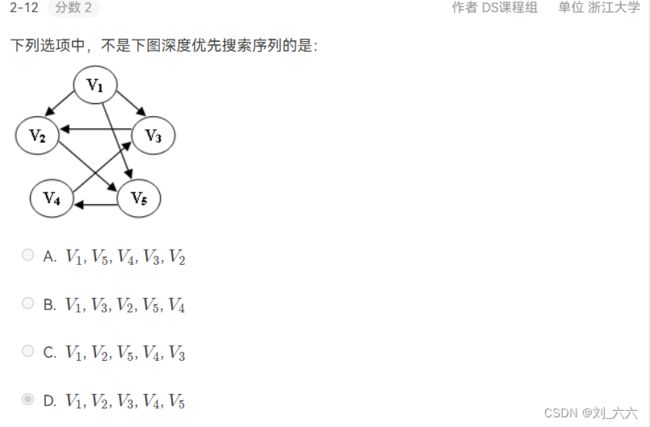
 还原有向图  深度优先遍历

 

 

 

 

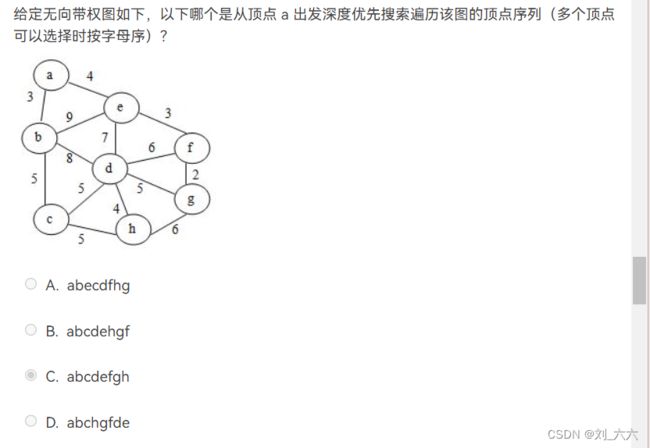
还原图 BFS

 

 

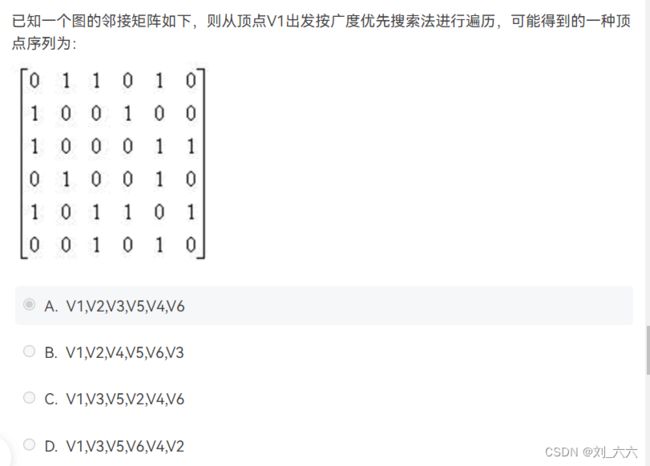
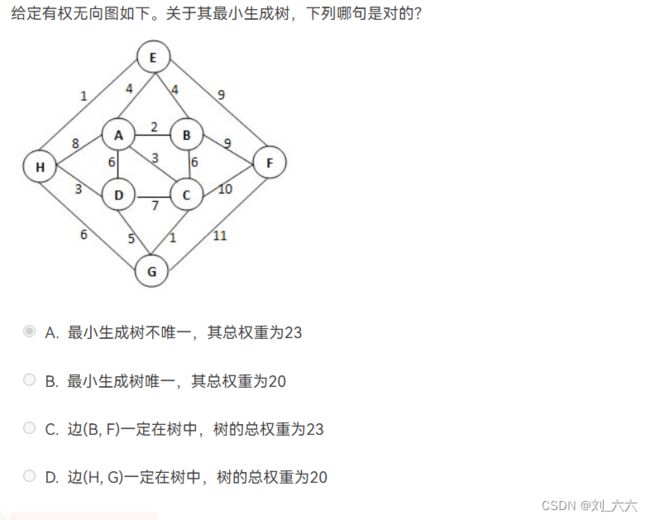
 还原图 用Prime或Kruskal求最小生成树算权重

 

 

首先最小生成树肯定不唯一  再者求最小生成树算权重