Tensorflow深度学习学习笔记

一、Tensorflow基础及深度学习原理

1.Tensorflow中网络搭建的三种方法

1.keras.models.Sequential()

适用于简单线性堆叠网络。
流程：创建Sequential()对象，逐层堆叠网络

import tensorflow as tf
from tensorflow.keras import layers, models

model = models.Sequential()

model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(32, 32, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))

model.summary()

也可以不使用.add方法。直接在Sequntial里放入层列表

import tensorflow as tf
from tensorflow.keras import layers, models

model = models.Sequential([
    layers.Conv2D(32, (3, 3), activation='relu', input_shape=(32, 32, 3)),
    layers.MaxPooling2D((2, 2)),
    layers.Conv2D(64, (3, 3), activation='relu'),
    layers.MaxPooling2D((2, 2)),
    layers.Conv2D(64, (3, 3), activation='relu'),
    layers.Flatten(),
    layers.Dense(64, activation='relu'),
    layers.Dense(10, activation='softmax')
])

model.summary()

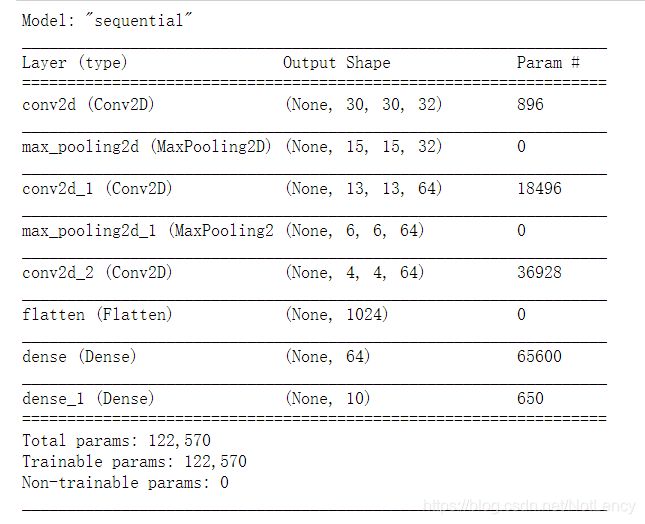
注意：input_shape=(32, 32, 3)，在模型搭建过程中会自动填空Batch维度，即None。而不需要在定义input_shape的时候进行定义。
第一列中的层名是按照层的类型默认1开始的序列后缀命名。

2.keras.models.Model()

如果我们像实现一些更为复杂的网络，比如多输入多输出的模型就需要使用到keras.models.Model()来构建网络。如下代码同时输出最后卷积层Flatten后提取的特征层，以及分类结构。
流程使用keras.Input定义输入张量shape， 创建网络层；定义每层的输入和输出张量；keras.models.Model确定输入张量和输出层，keras可以根据每一层的输入输出关系完成整个网络图的创建。

import tensorflow as tf
from tensorflow.keras import layers, models, Input

input_tensor = Input(shape=(32, 32, 3))
x = layers.Conv2D(32, (3, 3), activation='relu')(input_tensor)
x = layers.MaxPooling2D((2, 2))(x)
x = layers.Conv2D(64, (3, 3), activation='relu')(x)
x = layers.MaxPooling2D((2, 2))(x)
x = layers.Conv2D(64, (3, 3), activation='relu')(x)
output_tensor1=layers.Flatten()(x)
x = layers.Dense(64, activation='relu')(output_tensor1)
output_tensor2 = layers.Dense(10, activation='softmax')(x)

model = models.Model(inputs=input_tensor, outputs=[output_tensor1, output_tensor2])
model.summary()

3.继承类

在应对复杂结构的网络的时候，往往会按照采用自定义类（继承keras.models.Model）的方式来建立网络，使得整个网络结构更加规范整洁，同时通过call函数可以方便地处理复杂网络的输入输出关系。（有跟torch搭建思想借鉴的嫌疑）

import  tensorflow as tf
from    tensorflow import keras
from    tensorflow.keras import layers
from    tensorflow.keras.models import Model

class MyNet(Model):
    def __init__(self):
        super(MyNet, self).__init__()
        self.conv1 = layers.Conv2D(32, (3, 3), activation='relu')
        self.pool1 = layers.MaxPooling2D((2, 2))
        
        self.conv2 = layers.Conv2D(64, (3, 3), activation='relu')
        self.pool2 = layers.MaxPooling2D((2, 2))

        self.conv3 = layers.Conv2D(64, (3, 3), activation='relu')
        self.flatten = layers.Flatten()
        
        self.fc1 = layers.Dense(64, activation='relu')
        self.fc2 = layers.Dense(10, activation='softmax')
        
    def call(self, inputs):
        out = self.conv1(inputs)
        out = self.pool1(out)
        
        out = self.conv2(out)
        out = self.pool2(out)
        
        out = self.conv3(out)
        out = self.flatten(out)
        
        out = self.fc1(out)
        out = self.fc2(out)
        
        return out

def main():
    model = MyNet()
    model.build(input_shape=(None,32, 32,3))
    model.summary()

if __name__ == '__main__':
    main()

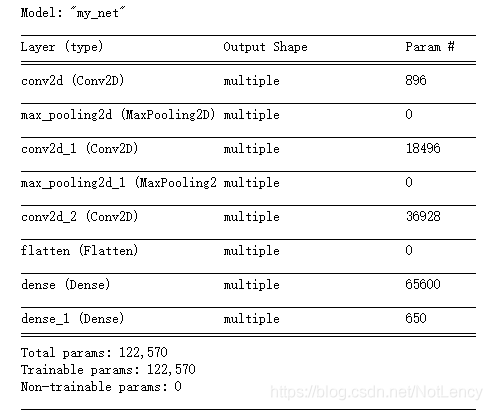
注意：这种方法需要在定义**input_shape=(None,32, 32,3)**时，考虑batch维度。
可以看出不是原生态的方法，导致summary的每层shape参数缺失。

7.Tensorflow中张量的合并与分割

import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

import tensorflow as tf

# 初始化两个张量
a = tf.ones([4, 35, 8])
b = tf.ones([4, 35, 8])

tf.concat()

# 将两个张量在指定维度上合并
c = tf.concat([a, b], axis=0)
print(c.shape)
print('\n')

输出：(8, 35, 8)
tf.stack()

# 新添一个维度，并在指定维度上将两个张量合并
c = tf.stack([a, b], axis=1)
print(c.shape)
print('\n')

输出：(4, 2, 35, 8)
tf.unstack()

# 在指定维度上将张量拆分成指定维度shape大小个张量
c = tf.unstack(c, axis=1)

print(len(c), c[0].shape)
print('\n')

输出：2 (4, 35, 8)
tf.split()

# 在指定维度上将张量拆分成指定大小和数量个张量
c = tf.split(c, axis=0, num_or_size_splits=[1, 1, 2])

print(len(c), c[0].shape)
print('\n')

输出：3 (1, 2, 35, 8)

8.张量数据统计

范数 tf.norm()

1.二范数：全部数值平方和再开平方

2.无穷范数：即所有数值中绝对值最大的

3.一范数：全部数值绝对值加和

tf.norm(指定张量, ord=2, axis=1) # ord用来指定所求的范数类型：1为一范数，2为二范数，默认为二范数；axis用来指定用来求范数的的张量维度，不写默认是对整个张量求值。

tf.reduce_min/max/mean/sum(张量, axis)
min() # 表示在输入的张量中选取其中最小的数值输出
max() # 表示输出最大的
mean() # 表示将所有元素加和然后求均值
sum() # 表示将所有元素加和
sum(张量a, 张量b) # 将两个张量所有元素相加
axis参数表示在指定的维度上求相应数据，不写默认是全部维度
（以上方法最后输出都是一个标量的值）

tf.argmax/argmin(张量, axis)
求出最大元素或者最小元素在张量中的位置。可以指定在某个维度上求解。

tf.equal(张量a, 张量b)
对张量a、b进行比较，相同的位置上置为1，不同为0；返回值是一个shape与a、b相同的张量。（用来比较预测值与实际值的相似度，以求精准度？）

tf.unique(张量a)
去除张量中的重复值

tf.sort/argsort(张量a, direction=‘ASCENDING’ or ‘DESCENDING’)
sort() #在每个维度上独立排序
argsort() # 输出相应位置，输出结果是张量中大小顺序排列的元素的index

tf.math.top_k(张量a, k)
top_k() # 返回张量中前k大的数

top-k accuracy

对于每一次预测只要预测值的前k个里面包含有真实值，那么预测的准确率就是100%
top-k accuracy的计算方式：

import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

import tensorflow as tf

# tf.random.set_seed(2467)  # 设置种子，保证每次随机产生的值都相同

def accuracy(output, target, topk=(1,)):
    maxk = max(topk)  # 取出topk中最大的数值，一次做好数据采取
    batch_size = target.shape[0]  # 获取样本的总数量用来计算正确率

    pred = tf.math.top_k(output, maxk).indices  # 获取到前 k 大的预测值得索引，此处的索引对应着物品的label
    pred = tf.transpose(pred, [1, 0])  # 转置一下
    target = tf.broadcast_to(target, pred.shape)  # 扩张张量的维度用以计算
    correct = tf.equal(pred, target)  # 预测与真实值相比较，相同的在对应位置上置为一

    res = []  # 用来接收结果
    for k in topk:
        correct_k = tf.cast(tf.reshape(correct[:k], [-1]), dtype=tf.float32)  # 根据不同的top_k的k值，获取不同范围的correct结果
        correct_k = tf.reduce_sum(correct_k)  # 计算一共有多少个物品在top_k的范围内预测正确
        acc = float(correct_k / batch_size * 100.0)  # 求准确率：这一批中预测正确的个数 / 一批的总个数 * 100%
        res.append(acc)  # 将计算结果加到返回结果中
        # for结束

    return res

output = tf.random.normal([1000, 10])  # 随机设置output的数值，作为预测值使用;一共1000个物品，每个物品预测值有10种可能
output = tf.math.softmax(output, axis=1)  # 随机设置output的数值，并使用softmax函数将物品的预测概率调整为总和为 1

# 使用均匀分布在 0-10 内生成output.shape[0]个整数，设置为真实值，代表在1000个物品中一共有10类物品
target = tf.random.uniform([output.shape[0]], maxval=output.shape[1], dtype=tf.int32)  
# print('prob:', output.numpy())
pred = tf.argmax(output, axis=1)
# print('pred:', pred.numpy())
# print('target:', target.numpy())

topk = (1,2,3,4,5)
acc = accuracy(output, target, topk)
print('top 1 - {0} acc : {1}'.format(len(topk), acc))

输出：
top 1 - 5 acc : [10.199999809265137, 20.700000762939453, 30.700000762939453, 40.400001525878906, 50.19999694824219]

9.数据的填充与复制

tf.pad()
tf.pad(张量a, [[头部填充的维度数， 尾部填充的维度数], ……, [头部填充的维度数， 尾部填充的维度数]])，默认填充为0。扩充张量的同时，在扩充的位置上添加数据。（卷积中的padding）
此方法常用于图片卷积处理和NLP自然语言处理（当一个句子的长度不同时，通过此方法让句子的长度变得相同）

# 张量中数据的填充与复制
a = tf.reshape(tf.range(9), [3, 3])
print(a)

# tf.pad(张量a, [[头部填充的维度数， 尾部填充的维度数], ……, [头部填充的维度数， 尾部填充的维度数]])，默认填充为0
a = tf.pad(a, [[1, 2], [1, 1]])  # 在行的头部添加 1 行，尾部添加 2 行；在列的头部添加 1 列，尾部添加 1 列
print(a)

输出：
tf.Tensor(
[[0 1 2]
[3 4 5]
[6 7 8]], shape=(3, 3), dtype=int32)
tf.Tensor(
[[0 0 0 0 0]
[0 0 1 2 0]
[0 3 4 5 0]
[0 6 7 8 0]
[0 0 0 0 0]
[0 0 0 0 0]], shape=(6, 5), dtype=int32)

tf.tile()

a = tf.reshape(tf.range(9), [3, 3])
# tf.tile(张量a, [在对应维度上复制的倍数, ……, 在对应维度上复制的倍数])；用来在维度层面上复制张量，复制之后的数据占用空间
a = tf.tile(a, [1, 2])  # 对张量a在行上面复制成原来的1倍，在列上面复制成原来的2倍
print(a)

输出：
tf.Tensor(
[[0 1 2]
[3 4 5]
[6 7 8]], shape=(3, 3), dtype=int32)
tf.Tensor(
[[0 1 2 0 1 2]
[3 4 5 3 4 5]
[6 7 8 6 7 8]], shape=(3, 6), dtype=int32)

tf.broadcast_to()
tf.broadcast_to(张量a, [填写扩充之后的张量的shape])，优点是它并没有真实的占用内存。
而且有些张量运算操作本身就支持并且会调用broadcast_to()方法，比如在计算[b, 784] + [784]时，自动会调用此方法将[784] -> [b, 784]，不用自己手动显视的调用broadcast_to()方法。

a = tf.reshape(tf.range(9), [3, 3])
a = tf.expand_dims(a, axis=0)
print(a)

aa = tf.tile(a, [2, 1, 1])
print(aa)

# tf.broadcast_to(张量a, [填写扩充之后的张量的shape])
bb = tf.broadcast_to(a, [2, 3, 3])
print(bb)

输出：
tf.Tensor(
[[[0 1 2]
[3 4 5]
[6 7 8]]], shape=(1, 3, 3), dtype=int32)
tf.Tensor(
[[[0 1 2]
[3 4 5]
[6 7 8]]

[[0 1 2]
[3 4 5]
[6 7 8]]], shape=(2, 3, 3), dtype=int32)
tf.Tensor(
[[[0 1 2]
[3 4 5]
[6 7 8]]

[[0 1 2]
[3 4 5]
[6 7 8]]], shape=(2, 3, 3), dtype=int32)

10.张量限幅

tf.clip_by_value(张量a, b, c)
张量a中所有处于(b, c)之间的数会被保留下来，其他数值会被置零。
类似的还有tf.maximum(张量a, b)和tf.minimum(张量a, b)方法，保留张量中大于b的（小于b的）所有数值，其他数值置零。

relu()
tf.nn.relu(张量a)这个方法等价于tf.maximum(张量a)，不过为了提高可读性我们都写前者。

tf.clip_by_norm(张量a, b)
根据二范数来放缩梯度, 保留梯度方向的同时，减少梯度对张量整体方向的影响。
此方法会把张量a的模缩放成b大小。

new_grads, total_norm = tf.clip_by_global_norm(张量a，b)
此方法用于等比例放缩神经网络各层的梯度张量(各层的梯度张量整合成张量a)，保证不会出现某层的梯度放缩比例太大或太小的问题，保证梯度的整体方向不发生改变。其中b的取值是>=梯度张量a中所有所有维度的二范数的加和。
返回值new_grads是经过缩放后的综合梯度张量a, total_norm是放缩前张量a中所有所有维度的二范数的加和。

Gradient Clipping

为了解决梯度爆炸(Gradient exploding)和梯度消失(Gradient vanishing)问题。
方式：避免出现梯度过大或者梯度过小的情况，如果出现了就使用tf.clip_by_global_norm(张量a，b)方法对梯度进行放缩。

new_grads, total_norm = tf.clip_by_global_norm(张量a，b)
此方法用于等比例放缩神经网络各层的梯度张量(各层的梯度张量整合成张量a)，保证不会出现某层的梯度放缩比例太大或太小的问题，保证梯度的整体方向不发生改变。其中b的取值是>=梯度张量a中所有所有维度的二范数的加和。
返回值new_grads是经过缩放后的综合梯度张量a, total_norm是放缩前张量a中所有所有维度的二范数的加和。

11.进阶操作

tf.where(张量a)
此方法中的张量a首先经过布尔转换，比如通过 a = a > 0 操作将张量a中所有大于 0 的元素为设置为真，返回值则为张量a中所有元素值为真的位置索引。

tf.scatter_nd(indices, updates, 张量a)
此方法是将update中的数值按照indices中的位置索引，逐一更新到 a 中。但是此方法只能在 a 中元素全部为 0 时使用。

tf.meshgrid()
确定坐标轴的区间及间隔大小，并生成坐标轴上的点，方便进行函数运算。

12.数据集加载

下面是小型、常用的数据集加载方法。
keras.datasets.XXX.load_data()
(x, y), (x_test, y_test) = tf.keras.datasets.XXX.load_data()
此方法适用于调用tensorflow中内含的数据集，例如：
boston housing(波斯顿房价)、mnist(手写数字)、fashion_mnist(服装)、cifar10/100(图片识别)、imdb(电影评分)。

(x, y), (x_test, y_test) = keras.datasets.cifar10.load_data()  # 读取cifar10的数据集

tf.data.Dataset.from_tensor_slices()

db = tf.data.Dataset.from_tensor_slices((x, y))  # 读取数据并转换成tensor格式
db = db.shuffle(10000)  # 可以对数据进行打乱操作，里面的参数是指打散的范围，10000就是指打散10000张图片。
db = db.batch(32).repeat(10)  # 用来划分训练数据的batchsize，batchsize=32;repeat()中的参数指的是整体数据集训练轮次epoch的次数，如果空着不填表示无穷大
batch = next(iter(db))  # 提取

一步完成读取的数据从numpy转换成tensor的格式

input pipeline

二、深度学习基础

Matmul矩阵形式到Neural Network形式的转换


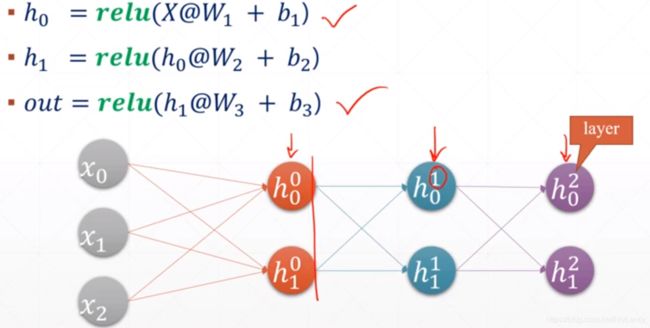
最一开始只是叫神经网络，还没有深度学习的概念，但当神经网络的层数多了就叫深度学习了。
（趣闻：最初时由于计算能力的限制，神经网络的解决问题的能力不如SVM方式，所以在2000年时机器学习领域SVM方案大行其道，而Neural Network由于缺乏一点可解释性，所以paper不是很好发。所以Geoffrey Hinton给一个较深的神经网络模型起了一个名字叫“Deep learning”，很多审稿人以为是一个新的概念，为了增大自己家刊物的知名度，就给通过了，而现在由于计算能力的大幅提升、数据量的暴增、激活函数解决梯度弥散，以及Dropout、Batchnormlization、超参数初始化研究的进步和ResNet的发明和引用，可以使得神经网络的层数变得很深，从而能力得到大幅提升，所以之后“Neural Network”就作为“Deep learning”被人们所熟知，也借此保留下来了名字。）

1.数据格式转换

神经网络对于不同的应用会有一个不同的输出格式要求，所以我们要通过一些方法来对我们的输出进行规格化。比如，在线性划分linear regression中我们的输出元素是实数out∈R（斜率和偏置的数值）；在分类中，out是每种label的概率值取值在[0，1]中，并且out中元素加和为1。

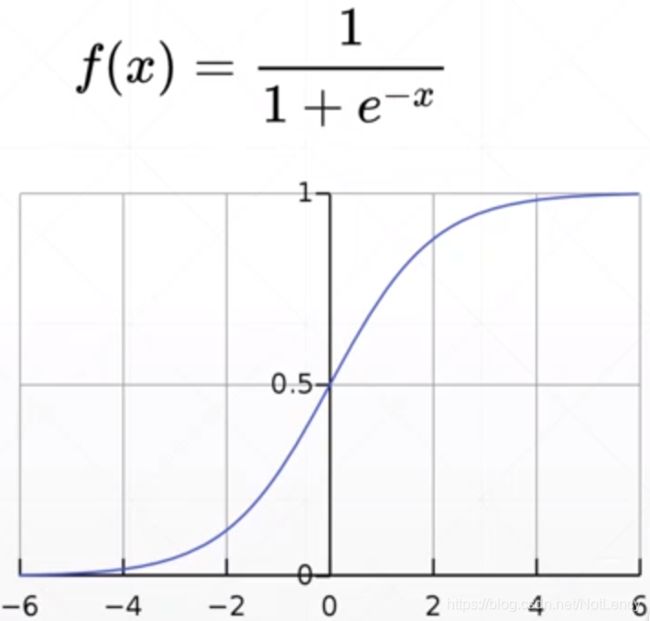
sigmoid()

tf.sigmoid()将输入的值转换到[0，1]之间。

softmax()

tf.nn.softmax()保证输出在[0，1]之间的同时，加和为1。在多分类时使用。

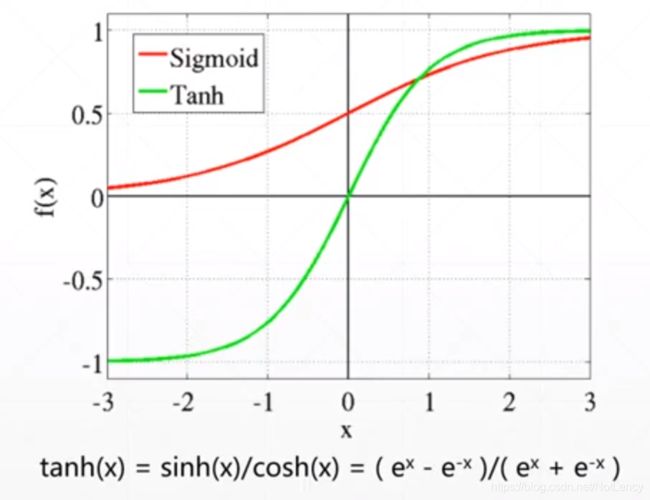
tanh()

输出值在[-1， 1]之间，它是将softmax()的输出放大了两倍，然后在乡下平移得到的。

2.损失函数loss

Mean Squared Error，MSE均方差

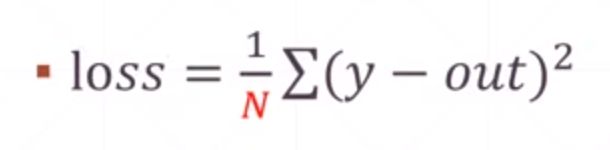
二范数

求MSE的三种方式：
tf.reduce_mean(tf.square(y-out))
tf.square(tf.norm(y-out)) / (out中元素的总个数)
tf.losses.MSE(y, out)

Cross Entropy交叉熵

Entropy信息熵

熵：衡量不确定度，衡量惊喜度的概念。
熵越低，意味着信息越多越不稳定。

（熵！信息居然也是可以量化的！）

Cross Entropy交叉熵

衡量两个信息之间的差异，差异越小交叉熵越小（预测与真实值越接近）。

tf.losses.binary_crossentropy(y, logits, from_logits=True) # out不经过激活函数激活时名字叫logits

为什么不继续使用MSE而选择Cross Entropy？？？

sigmoid + MSE方式会出现一个梯度消失的问题，因为sigmoid函数在两端的变换比较平缓。而交叉熵则收敛的很快。

Hinge Loss

用在SVM中，求最“胖”的那条线。

3.梯度

SGD、Monmentum、NAG、Adagrad、Adadelta、RMSprop

1.什么是梯度

梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

2.为什么梯度方向是函数增长最快的方向？

https://blog.csdn.net/weixin_42398658/article/details/83017995
TIPs：从如何找出函数增大速度最快的方向为出发点，去寻找答案。而不是一开始就想“为什么梯度方向是函数增长最快的方向？”。

3.梯度的意义，怎么利用梯度？

既然我们知道了梯度是使得函数增长最快的方向，那么其反方向就是使得函数下降最快的方向，这样我们就有办法更新各个超参数使得loss函数取得最小值了。
参数更新：

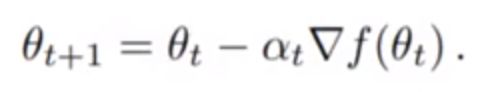
θ：超参数
α：学习率，也可以用lr表示
▽f(θ)：梯度

5.自动求解梯度

    # 构建梯度环境，将w和b加入跟踪列表
    with tf.GradientTape() as tape:
        tape.watch([w1, b1])
        # 构建计算函数
        loss = ((w1 * x1 + b1) - y1) ** 2
    # 求导
    [dloss_dw1, dloss_db1] = tape.gradient(loss, [w1, b1])
    del tape

4.激活函数

常见的激活函数的总结：
https://blog.csdn.net/tyhj_sf/article/details/79932893
https://zhuanlan.zhihu.com/p/192497127?utm_source=wechat_timeline

5.反向传播

查看https://www.bilibili.com/video/BV1HV411q7xD?from=search&seid=10919896531854962895教程P67~69,讲得很清楚。

6.tf.keras中的工具

1.datasets，layers，losses，metrics

# 用metrics来总体衡量模型训练过程中的相关数值。
loss_meter = metrics.Mean()
loss_meter.reset_states()  # 使用之前先清零

loss_meter.update_state(loss)  # 更新loss
print('epoch={0},step={1},loss={2}'.format(epoch, step, loss_meter.result().numpy()))

# 设置一定间隔来清除缓存，可以是几个step，也可以是1个epoch
loss_meter.reset_states()

acc_meter = metrics.Accuracy()
acc_meter.reset_states()  # 使用之前先清零

acc_meter.update_state(y, pred)  # y真实值，pred预测值
print('epoch={0},step={1},acc={2}'.format(epoch, step, acc_meter.result().numpy()))

# 设置一定间隔来清除缓存，可以是几个step，也可以是1个epoch
acc_meter.reset_states()

5.optimizers

optimizer = optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.99)
optimizer = optimizers.SGD(lr=0.001, momentum=0.9)  # momentum的数值一般设置为0.99,0.9或0.5
optimizer = optimizers.RMSprop(lr=0.001, momentum=0.9)

6.compile

# 使用compile来设置模型的相关参数
model.compile(optimizer=optimizers.Adam(lr=0.01),  # 指定梯度下降优化器和学习率
              loss=tf.keras.losses.CategoricalCrossentropy(from_logits=True),  # 设置loss函数
              metrics=['accuracy'])  # 指定一个测试模型的评测标准

7.fit、evaluate

@enable_multi_worker
  def fit(self,
          x=None,  # x：输入数据。如果模型只有一个输入，那么x的类型是numpy，array，如果模型有多个输入，那么x的类型应当为list，list的元素是对应于各个输入的numpy array
          y=None,  # y：标签，numpy array。x和y可以作为张量输入（x， y）
          batch_size=None,  #batch_size：整数，指定进行梯度下降时每个batch包含的样本数。训练时一个batch的样本会被计算一次梯度下降，使目标函数优化一步。
          epochs=1,  # epochs：整数，训练终止时的epoch值，训练将在达到该epoch值时停止，当没有设置initial_epoch时，它就是训练的总轮数，否则训练的总轮数为epochs - inital_epoch
          verbose=1,  # verbose：日志显示，0为不在标准输出流输出日志信息，1为输出进度条记录，2为每个epoch输出一行记录
          callbacks=None,  # callbacks：list，其中的元素是keras.callbacks.Callback的对象。这个list中的回调函数将会在训练过程中的适当时机被调用，参考回调函数
          validation_split=0.,  # validation_split：0~1之间的浮点数，用来指定训练集的一定比例数据作为验证集。验证集将不参与训练，并在每个epoch结束后测试的模型的指标，如损失函数、精确度等。注意，validation_split的划分在shuffle之前，因此如果你的数据本身是有序的，需要先手工打乱再指定validation_split，否则可能会出现验证集样本不均匀。
          validation_data=None,  # validation_data：形式为（X，y）的tuple，是指定的验证集。此参数将覆盖validation_spilt。
          shuffle=True,  # shuffle：布尔值或字符串，一般为布尔值，表示是否在训练过程中随机打乱输入样本的顺序。若为字符串“batch”，则是用来处理HDF5数据的特殊情况，它将在batch内部将数据打乱。
          class_weight=None,  # class_weight：字典，将不同的类别映射为不同的权值，该参数用来在训练过程中调整损失函数（只能用于训练）
          sample_weight=None,  # sample_weight：权值的numpyarray，用于在训练时调整损失函数（仅用于训练）。可以传递一个1D的与样本等长的向量用于对样本进行1对1的加权，或者在面对时序数据时，传递一个的形式为（samples，sequence_length）的矩阵来为每个时间步上的样本赋不同的权。这种情况下请确定在编译模型时添加了sample_weight_mode=’temporal’。
          initial_epoch=0,  # initial_epoch: 从该参数指定的epoch开始训练，在继续之前的训练时有用。
          steps_per_epoch=None,
          validation_steps=None,
          validation_batch_size=None,
          validation_freq=1,  # 设置每多少个epoch进行一次验证
          max_queue_size=10,
          workers=1,
          use_multiprocessing=False):

fit函数返回一个History的对象，其History.history属性记录了损失函数和其他指标的数值随epoch变化的情况，如果有验证集的话，也包含了验证集的这些指标变化情况

# 使用fit来设置训练所用数据和训练轮次epoch,指定验证时所用的数据集，以及模型训练多少步step进行一次验证
model.fit(db, epochs, validation_data=db_val,
          validation_freq=2)  # 使用这个方法验证模型validating的过程是在模型training的过程中进行的（推荐使用这个方法，因为你不知道你的模型到底要training多久）
model.evaluate(db_val)  # 在模型training结束后调用，开始进行验证

8.predict

# 使用predict来测试模型或者直接输入验证集
pred = model.predict(x) 
pred = model(x)

9.自定义网络

10.模型的保存与加载

# 模型的保存与加载
# 1.只保存模型的参数
model.save_weights(dir)
model = create_mdoel()  # 创建一个和之前的模型结构完全一致的模型,然后加载保存下来的参数
model.load_weights(dir)

# 2.全部保存
model.save('model.h5')
print('saved total model.')
model = tf.keras.models.load_model('model.h5')

# 3.更加通用的保存方式，可以提供给其他语言使用
tf.saved_model.save(model, dir)
imported = tf.saved_model.load(dir)
model = imported.signatures['serving_default']

7.过拟合与欠拟合

1.Underfitting，欠拟合

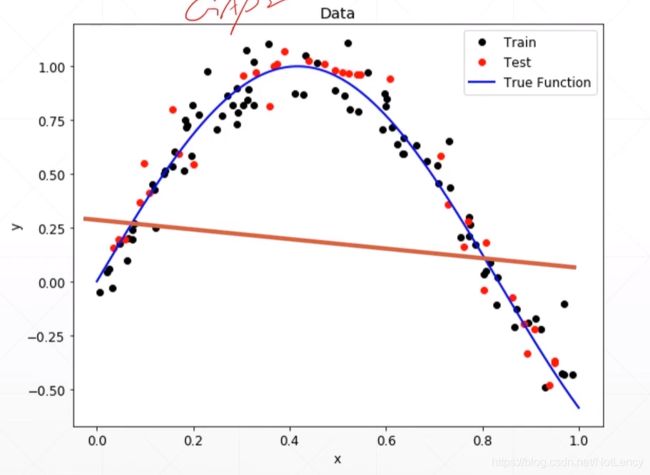
所用的模型不够复杂。——增加层数，增加参数。
训练准确度和验证准确度都很差。

2.Overfitting，过拟合

模型过于复杂。——减少层数，减少参数
训练准确度很高，但验证准确度很差。泛化能力差。

1.交叉验证，为什么要将Dataset划分为trian_db，val_db，test_db？

答：train_db用于梯度下降更新模型参数的过程；
从狭义来讲，验证集val_db并没有参与梯度下降确定参数的过程，也就是说是没有经过训练的，但从广义上来看，验证集val_db却参与了一个“人工调参”的过程——我们根据验证集的结果调节了迭代数、调节了学习率，查看是否发生了过拟合情况等等，使得结果在验证集上最优。
因此，我们也可以认为，验证集也参与了训练。所以，我们还额外需要一个test_db，一个完全没有参与过模型训练的数据集来测试我们的模型。

2.划分比例和方法

10=6:2:2
采用动态划分train_db和val_db的方式会有提升，每次选用不同的val_db来验证模型，尽可能的让更多的数据参与到训练中。

# 使用model.fit()通过设置参数可以直接实现交叉验证的功能
model.fit(nontest_db,
	batch_size=batchsize,
	epochs=epoch,
	shuffle=True,
	validation_split=0.1  # 设置划分训练集和验证集的比例
	validation_freq=1)

3.减轻过拟合

1.尽可能的提供更多的数据
2.尽可能低的模型复杂度；在建立模型时首先设置较高的模型复杂度，查看过拟合情况，然后在主动降低复杂度。
3.数据增强（变相的增加训练数据）
4.Early Stopping提前停止训练（这不就是较少的epoch吗？）

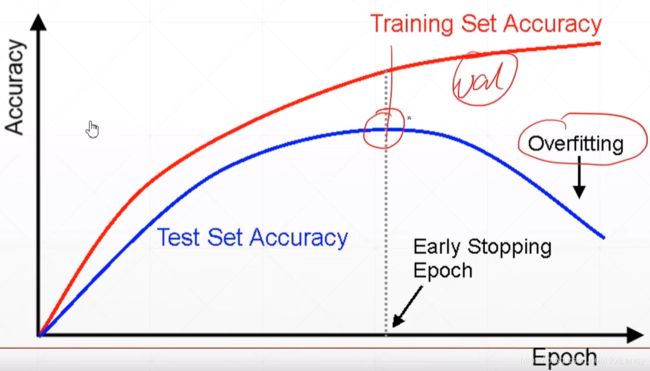
5.Regularization正则化（Weight Decay权值衰减）
将模型的超参数的范数整合到模型的loss方程中得到loss2方程，在梯度下降求loss2最小值。loss2 = loss + λ（因子）× 模型超参数的范数，其最小值等于两者的最小值，当第二项（λ（因子）× 模型超参数的范数）最小时也就限制了模型的复杂度。


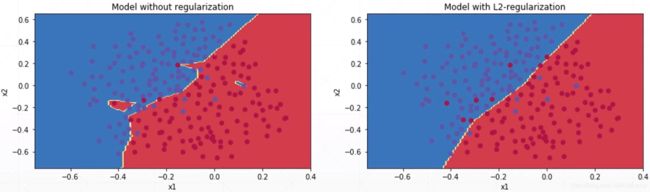
常用的两种正则化方式方程表达，loss函数=J(θ)

6.Dropout(Learning less to learn better)

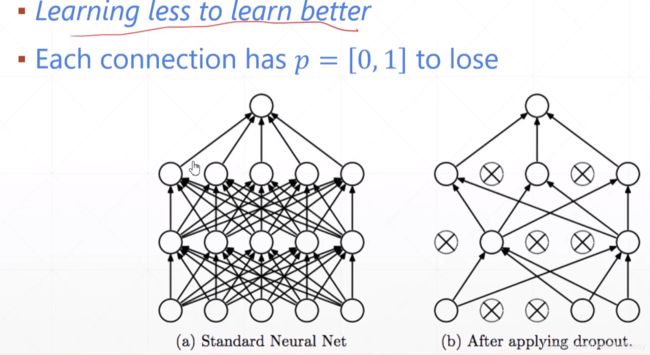
8.动量与学习率

1.Momentum，动量

梯度下降时加入了上一次下降方向的影响。

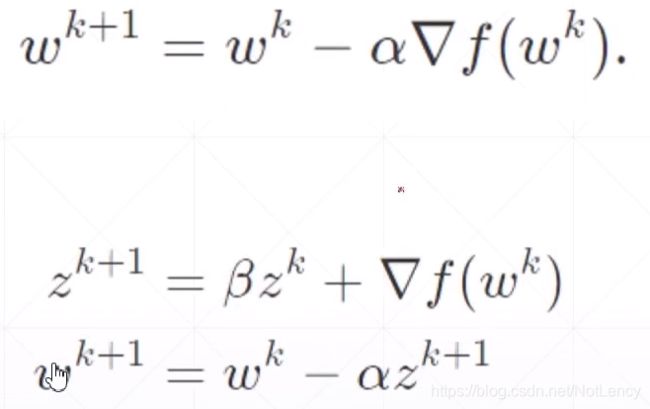
不加入动量

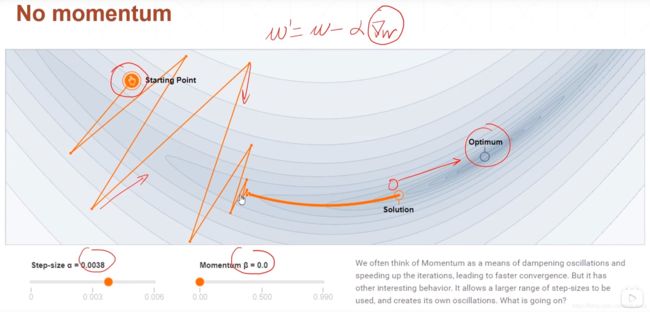
加入动量

# 设置优化器
optimizer = optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.99)
optimizer = optimizers.SGD(lr=0.001, momentum=0.9)  # momentum的数值一般设置为0.99,0.9或0.5
optimizer = optimizers.RMSprop(lr=0.001, momentum=0.9)

2.学习率

1.学习率下降/学习率衰减

# 设置学习率衰减
optimizer = optimizers.RMSprop(lr=0.001, momentum=0.9)
for epoch in range(100):
    optimizer.learning_rate = 0.2 * (100 - epoch) / 100

initial_learning_rate = 0.1
learning_rate = tf.train.exponential_decay(initial_learning_rate,  # 初始学习率
                                           global_step=global_step,  # 全局步数，系统会自动更新这个参数的值，从1开始，每迭代一次加1。
                                           decay_steps=10,  # 为衰减速度，每10步一衰减
                                           decay_rate=0.5)  # 为衰减率（取值0到1）

9.神经网络的类型

1.Dense，全连接层（线性层）

（名字由来：因为每一个输入节点和所有的输出节点相连接，连接的密度很Dense）

Multi-layer，使用容器的创建

model = tf.keras.Sequential([
    tf.keras.layers.Dense(128, activation='relu'),
    tf.keras.layers.Dense(64, activation='relu'),
    tf.keras.layers.Dense(10)
])

model.build(input_shape=[None, 512])
model.summary()

输出：
Model: “sequential”
Total params: 74,570
Trainable params: 74,570
Non-trainable params: 0

2.Convolutional Neural Networks, CNN卷积神经网络，什么是卷积？

卷积相比于原来的全连接层大大降低了参数的数量。
不同的卷积核有不同的效果：

1.为什么说卷积神经网络是“不可解释的”？（这是一个大问题，我的答案还是很片面）

答：因为虽然我们列举了一些卷积核像上述例子一样具有一些特定的作用，可是他们只是用在图片处理中来进行一些确切的、有目的的操作。
而在深度学习里面存在有大量的卷积核的初始数值是随机设定的，并通过梯度下降进行更新，我们只知道在数学规则的约束下，通过参数更新使得我们的神经网络模型向着正确的、我们所希望的方向进行改变。但这些大量的、看起来是随机生成并通过梯度下降进行更新的卷积核，其真实的作用究竟是什么？我们人还没有一个清楚的认识，所以说目前的卷积神经网络是“不可解释的”。

延伸：神经网络的可解释性
还有就是为什么卷积核的大小是3 * 3、5 * 5，仅仅是因为他们最后的acc比较高吗？
神经网络的层数和准确率之间有什么关系？我们只能通过“先建模型看结果”来调整层数吗？
是否有办法“一眼”看出该用几层网络，用什么网络，学习率设置为多少等等需要用经验来确定的数值呢？
……

说神经网络是“黑箱”，其含义至少有以下两个方面：
一、神经网络特征或决策逻辑在语义层面难以理解
二、缺少数学工具去诊断与评测网络的特征表达能力（比如，去解释深度模型所建模的知识量、其泛化能力和收敛速度），进而解释目前不同神经网络模型的信息处理特点。

2.卷积神经网络中的一些计算

每一层的过滤器filter形状：[f, f, c, m] # [卷积核尺寸, 卷积核尺寸, 输入图片的通道数, 卷积核个数]
步长stride：s
填充padding：p
下采样/池化pooling：[b, b]，移动步长s1 # [池化核尺寸, 池化核尺寸]
上采样：[b, b]，移动步长s1
池化前、卷积前的图片大小：[n, h, w, c] # h = w，一般是相等的，可以不等
池化前、卷积后的图片大小：[n, h1, w1, c1] # h1 = w1，一般是相等的，可以不等

图片池化之前[n, h, w, c]，池化核形状[b, b]，步长s1，池化后 ===》[n, h1, w1, c]，其中
h1 = w1 = (h - b) / s1 + 1

图片卷积之前[n, h, w, c]，填充padding大小为p，采用步长s，通过卷积核[f, f, c, m]后 ===》[n, h1, w1, m]，其中h1 = w1 = floor((h + 2p − f ) / s + 1)
可以通过公式让h1 = h，然后反求出所需的padding的大小，以满足卷积之后图片大小不变的要求。

（一般来说卷积神经网络中卷积核和图片都是正方形的，但可以不是；在x和y方向上的填充尺寸以及步长大小，也都是相同的，但可以不是。）

3.经典的卷积神经网络模型

1.LeNet5

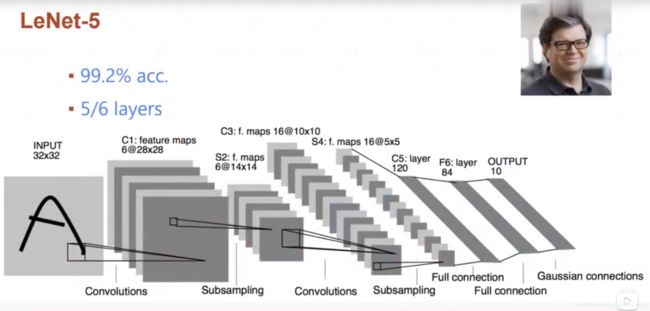
作者：Yann LeCun
年份：1998
层数：6层（不包括输入输出）
这个模型当年是跑在CPU上的。第一个较为成功的、应用于数字识别问题的卷积神经网络。LeNet的实现确立了CNN的结构，现在神经网络中的许多内容在LeNet的网络结构中都能看到，例如卷积层，Pooling层，ReLU层。LeNet-5 模型是 Yann LeCun 教授于 1998 年在论文 Gradient-based learning applied to document recognitionr中提出的，在 MNIST 数据集上， LeNet-5 模型可以达到大约 99.2%的正确率。

2.AlexNet

作者：G.Hinton和他的学生Alex Krizhevsky
年份：2012
层数：7层
出于显存的限制，不得已将模型的训练任务划分到了两个显卡上，所以模型看起来“裂开了”，现在计算能力比较强，又有了分布式计算的框架，已经不需要了使用这种结构的模型了。
比较创新的点是：1.使用了最大池化；2.引入了ReLU激活函数；3.Dropout

3.VGG

作者：Oxford Visual Geometry Group
年份：2014
层数：11~19层
VGG一共有6个版本（A-E）比如VGG16、VGG19
比较创新的点是：1.发现了在卷积中使用尺寸较小的核心效果比较好，因为尺寸越大卷积神经网络的参数量和复杂度就越接近全连接层，而小核心不仅可以降低参数量还可以提升效果（原因不知，只知道结果变好了）。
VGG模型在迁移学习中有较好的表现，好于同年竞赛的冠军GoogLeNet。

4.GoogLeNet

作者：Google
年份：2014
层数：22层
GoogLeNet是google推出的基于Inception模块的深度神经网络模型，在2014年的ImageNet竞赛中夺得了冠军，在随后的两年中一直在改进，形成了Inception V2、Inception V3、Inception V4等版本。
比较创新的点：1.使用了不同大小的卷积核、pooling层，然后将其处理后的结果综合起来进行考虑。

是不是通过简单的堆叠层数就可以提高模型的准确度了？答案是否定的，但是ResNets做到了！

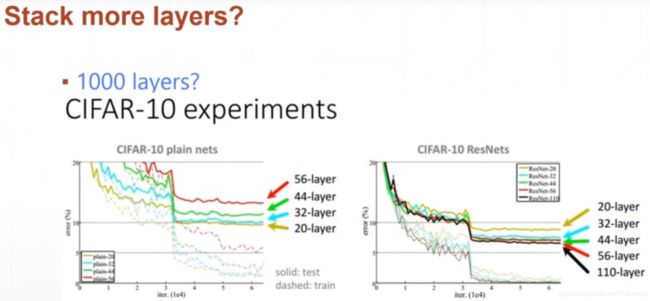
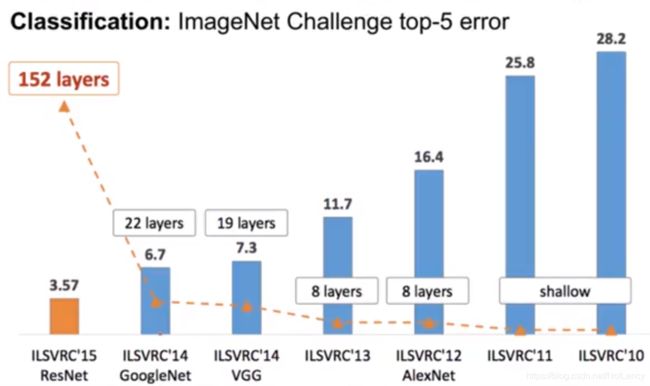
5.ResNet，深度残差网络

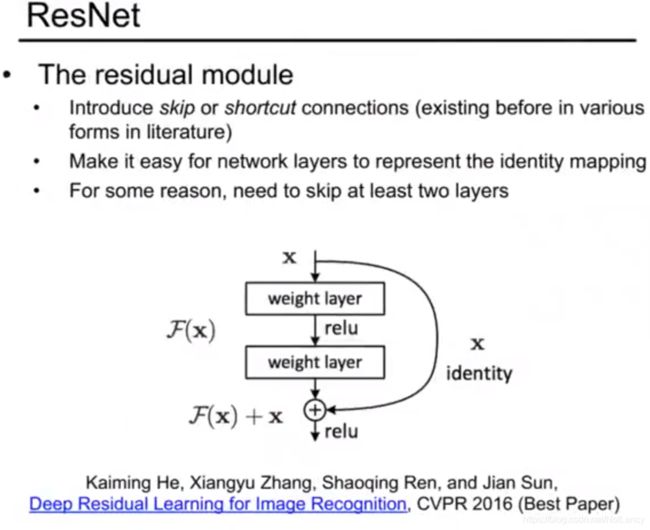
作者：Microsoft Research，微软研究团队包括何恺明、张祥雨、任少卿和孙剑四位成员
年份：2015年
亮点：在2015年的ImageNet大规模视觉识别竞赛（ImageNet Large Scale Visual Recognition Challenge, ILSVRC）中获得了图像分类和物体识别的优胜。 残差网络的特点是容易优化，并且能够通过增加相当的深度来提高准确率。其内部的残差块使用了跳跃连接，选择性的跳过某些网络结构，并且在整个网络稳定后再进行利用，缓解了在深度神经网络中增加深度带来的梯度消失问题，也保证了更深层次的网络的表现能力不会差于浅层的网络模型。

6.DenseNet

类似于ResNet的思想，ResNet的重点在于前一层的结果与下一层的输出有一条shortcut，可以直接作为下下层的输入相连接，而DenseNet则是前面的层与后面的所有层都有直接的shortcut，可以和后面的所有层都直接连接。而且在ResNet中前一层的结果和下一层的输出相结合的方式是直接相加，在DenseNet中则是以Concatenate操作相连接的，将前面的层的结果和后续层的结果并在一起作为输入，这样越后面的层其输入数据的channel就会越来越大。。

7.Inception

8.Xception

9.各神经网络的对比

各神经网络在准确率以及准确率与参数量上的对比：

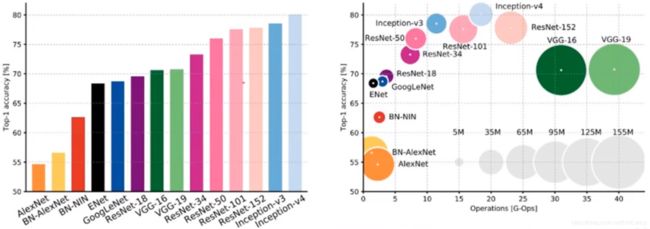
VGG的模型参数量大且准确率对不起他的大小。
以大小和准确率综合考虑比较好的是：
T0：Inception-V3
T1：Inception-V4和ResNet-101
T2：ResNet-50

3.Batch Normalization，BN层

1.Batch Normalization
我们以前在神经网络训练中，只是对输入层数据进行归一化处理，却没有在中间层进行归一化处理。要知道，虽然我们对输入数据进行了归一化处理，但是输入数据经过σ ( W X + b ) σ(WX+b)σ(WX+b)这样的矩阵乘法以及非线性运算之后，其数据分布很可能被改变，而随着深度网络的多层运算之后，数据分布的变化将越来越大。如果我们能在网络的中间也进行归一化处理，是否对网络的训练起到改进作用呢？答案是肯定的。
这种在神经网络中间层也进行归一化处理，使训练效果更好的方法，就是批归一化Batch Normalization（BN）。
简而言之，通过数学转换改变训练所用数据的分布，并使其尽可能的按着能够使得模型预测的更准的方式分布。一种数据归一化方式
查看https://www.bilibili.com/video/BV1HV411q7xD?from=search&seid=10919896531854962895教程P106~107,讲得很清楚。
如何进行Batch Normalization呢？只需添加BatchNormalization层就好了。

# BatchNormalization层
# 简而言之，通过数学转换使得训练所用的数据其分布尽可能的按着能够使得模型更准确的方式分布。
# 个人感觉属于数据预处理的一种
optimizer = optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.99)
bn_layer_net = layers.BatchNormalization(
	axis=-1,  # 指定在输入数据的哪一个维度上进行处理
	center=True,  # 转变数据分布后的数据分布中心位置
	scale=True,  # 转变数据分布后的数据的放大倍数
	trainable=True  # 设定center参数和scale参数是参与到反向传播中的
	)
x = tf.random.normal([2,4,4,3],mean=1.,stddev=0.5)  # 随机初始化一些服从（1.0，0.5）正态分布的数据进行测试
for i in range(100):  # 进行100轮的训练，并反向传播进行训练模型中的center和scale参数
    out = bn_layer_net(x,trainable=True)
    with tf.GradientTape() as tape:
        loss = tf.reduce_mean(tf.pow(out, 2)) - 1  # 此处的loss函数是随便写的；如果想要直接使训练数据的分布尽可能按着能够使得模型预测的更准确的方式进行分布，则可直接使用整个的模型loss函数来进行梯度下降调整参数
    grads = tape.Gradient(loss, bn_layer_net.trainable_variables)
    optimizer.apply_gradients(zip(grads, bn_layer_net.trainable_variables))

BatchNormalization层的优点：
1.能够保证神经网络每层的输入参数在经过激活函数的处理后都能产生一个较好的梯度。
2.鲁棒性更强
3.保证梯度的健康度，加快训练速度
4.可以省去dropout，L1, L2等正则化处理方法
5.提高模型训练精度

4.Recurrent Neural Network, RNN循环神经网络

CNN网络用是针对于自然界中二维的位置相关信息的提取，它采取位置相关、权值共享的思想，通过移动一个个窗口成功的提取出了有用信息的同时相比于FC网络大大降低了参数的数量。
但是，在信息的种类中不仅仅有位置相关的类型还有许多类型，比如时间相关（时序相关）类型，像语音、视频、音乐、聊天中的文字等等，我们将拥有时间相关特性的信息统称为：“Sequence序列”，接下来我们就来学习怎样对序列的信息进行提取和处理。

1.SimpleRNN

1.如何对非数字信息进行数字编码？Sequence embedding

例如翻译系统，我们怎样表示一个个句子？——拆成一个个单词。怎样表示单词？——使用数字编码。怎样对一个个单词进行编码？要注意数字是有大小关系的，会影响模型的处理，而实际中单词之间可没有大小关系但是有语义相关性。
如何对非数字信息进行编码而且还能保持其原有的语义相关性？
相似度，欧氏距离或者其他距离类型。

先把单词随意（方便进行存储、管理和运算的某种方式，比如要想办法减少占用的存储空间之类的）编码成一个数字，然后通过某种Word embedding方法将代表单词的数字再转化成向量，之后再利用向量之间的各种距离（机器学习中各种距离公式）来计算并更改表示各个单词的向量，最终使得两种语言中所表示意思相近的单词向量之间的距离越来越短。

Word embedding方法中现在已经有了的，比较好用的有：Word2Vec、GloVe。

2.如何处理句子中单词间的关系？

通过1中的方法，我们可能已经可以很好的将两种语言间相似意思的单词进行转化。但是只是单词的变换的话，这不就是所谓的“机翻”嘛，效果我们都知道是什么样的。所以，我们不仅要知道每个单词之间的相互转化，而且还要了解到这个单词在这个句子中所起的作用，这个单词的意思对整个句子语义的影响。


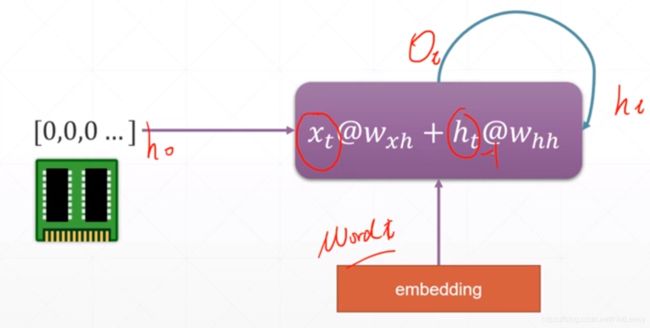
因此，在翻译句子的时候我们有了一个Consistent memory（持续性记忆）的概念，通过这种方法来把每个单词的意思糅合到整个句子中。
我们初始化一个句子状态h0，在对第一个单词进行处理的时候把h0也作为一个输入参与到其中，结果作为h1输入到第二个单词的处理过程中，得到h2，后续相同。其中，每一个hi都包含有前面单词的信息，最终我们得到的输出h5(hout)也就包含并糅合的句子中所有单词的信息，然后在对句子的语义进行判断。从h1到h5的过程也表现出了时间移动的这一特点，一句话时间越长包含的单词也就越多。


以SimpleRNN的数学公式为例，SimpleRNN的梯度表示：


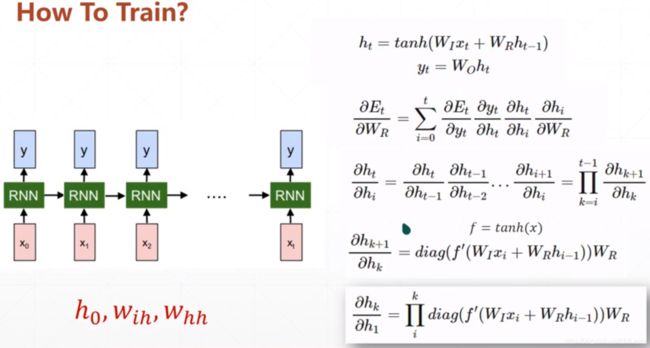
由于梯度的表示中存在Wr的累乘，所以会导致RNN中的一系列问题。

3.RNN的梯度弥散和梯度爆炸问题

首先需要明确的是，RNN 中的梯度消失/梯度爆炸和普通的 MLP 或者深层 CNN 中梯度消失/梯度爆炸的含义不一样。MLP/CNN 中不同的层有不同的参数，各是各的梯度；而 RNN 中同样的权重在各个时间步共享，最终的梯度 g = 各个时间步的梯度 g_t 的和。
由上所述的原因，可得RNN 中总的梯度是不会消失的。即便梯度越传越弱，那也只是远距离的梯度消失，由于近距离的梯度不会消失，所有梯度之和便不会消失。RNN 所谓梯度消失的真正含义是，梯度被近距离梯度主导，导致模型难以学到远距离的依赖关系。

由于梯度的表示中存在Wr的累乘，所以会导致RNN中的一系列问题。

当Wr<1时，高阶指数运算过后会导致梯度的数值无限接近于0（梯度弥散）；反之，当Wr>1时，梯度又会变得无穷大∞（梯度爆炸）。
梯度爆炸很容易解决，将梯度进行限幅：先用梯度除于自己的模，防止梯度数值太大，然后再乘一个常数a起到放大的作用。这就是所谓的梯度限幅Gradient clipping。
代码如下：

with tf.GradientTape() as tape:
    logits = model(x)  # 模型的预测结果
    loss = criteon(y, logits)  # loss函数

grads = tape.gradient(loss, model.trainable_variables)  # 求解梯度
# Gradient cliping，梯度限幅
grads = [tf.clip_by_norm(g, 15) for g in grads]  # 将梯度限幅到0~15之间,15是一个经验值，因为大多数较好的模型在训练的时候梯度的值一般在10上下。
optimizer.apply_gradients(zip(grads, model.trainable_variables))

梯度弥散的问题我们引入了Long-Short Term Memory。

2.LSTM，Long-Short Term Memory

我们在普通CNN网络中设置了一个“记忆单元”，它理应记录所有的单词语义，可是在实际应用中，他只能记住很近的几个单词所以叫Short Term Memory，而

遗忘门或者叫记忆门：将通过上一个循环计算出的h_t-1这个循环中输入的信息x_t通过参数W_f整合加偏置后在经过sigmoid函数归一化得到的f_t与之前的记忆C_t-1相乘完成之前记忆的一部分处理工作。因为得到的f_t经过了sigmoid函数的处理，其中的数值肯定是处于0~1之间的，所以他决定了上一次的记忆C_t-1还“记”着多少。

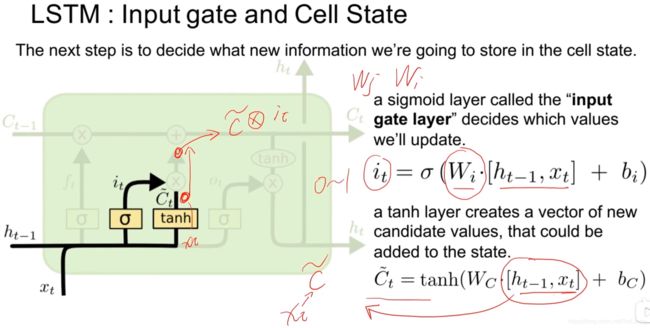
输入门：i_t表示对输入数据的开门程度，决定多少比例的数据用于输入，通过用参数W_i将上一循环的h_t-1和这次循环输入的x_t相整合，加上偏置后通过sigmoid函数激活得到介于0~1的数值。
~C_t表示经过tanh激活函数激活后的输入信息，其中数学运算过程如上例，不再赘述。
i_t与~C_t相乘得到本次循环的输入信息。

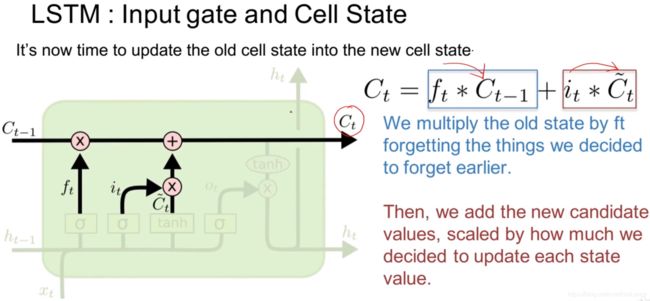
记忆门：将经过处理的历史记忆f_t * C_t-1与当前输入信息i_t * ~C_t相加和得到最终本轮的记忆C_t。

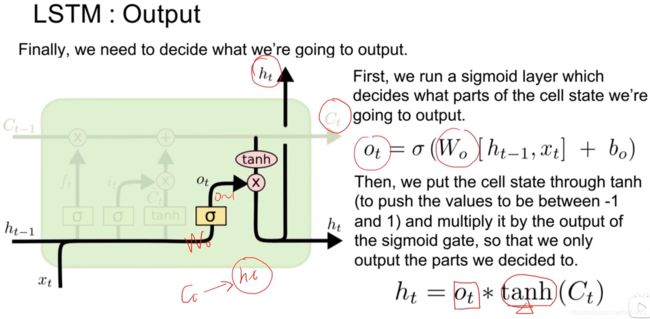
输出门：首先确定一个开门的程度o_t，然后与通过tanh激活的本循环记忆C_t相乘得到h_t
总览：

那么为什么LSTM能处理梯度弥散问题呢？

LSTM 刚提出时没有遗忘门，或者说相当于f_t = 1，这时候在C_t-1 -> C_t这条直接相连的短路路径上，梯度可以无损地向后传递，从而这条路径上的梯度畅通无阻，不会消失。类似于 ResNet 中的残差连接。
而且LSTM在求导的时候不会单独的出现W_r的n次方形式了，转而是各条路径上梯度相加的形式，虽然在路径上依然会出现参数累乘的情况，但是最终的梯度还要相加起来，这样就减轻了单独使用RNN时梯度弥散的情况。由于总的远距离梯度 = 各条路径的远距离梯度之和，即便其他远距离路径梯度消失了，只要保证有一条远距离路径（就是上面说的那条高速公路）梯度不消失，总的远距离梯度就不会消失（正常梯度 + 消失梯度 = 正常梯度）。因此 LSTM 通过改善一条路径上的梯度问题拯救了总体的远距离梯度。但是在爆炸的时候依然会爆炸（正常梯度 + 爆炸梯度 = 爆炸梯度）

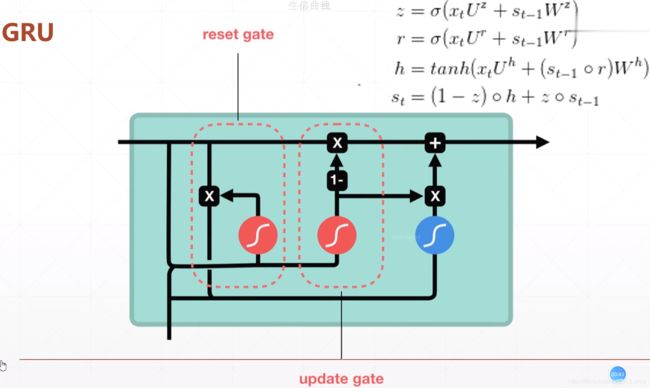
3.Gated Recurrent Unit，GRU

简化版的LSTM模型，复杂度降低了，性能更好了：

4.总结

其实RNN中用来解决梯度弥散的门结构优点类似于ResNet中的残差网络结构。

5.GNN，图神经网络

10.Unsupervised Learining，无监督学习

强化学习（行为主义）：强化学习是智能体（Agent）以“试错”的方式进行学习，通过与环境进行交互获得的奖赏指导行为，目标是使智能体获得最大的奖赏，强化学习不同于连接主义学习中的监督学习，主要表现在强化信号上，强化学习中由环境提供的强化信号是对产生动作的好坏作一种评价(通常为标量信号)，而不是告诉强化学习系统RLS(reinforcement learning system)如何去产生正确的动作。由于外部环境提供的信息很少，RLS必须靠自身的经历进行学习。通过这种方式，RLS在行动-评价的环境中获得知识，改进行动方案以适应环境。通过这种方法训练的模型所使用的数据量很小。
监督学习：把已经人工分好类的做好标签的数据输入到模型中去，让模型学习数据之间存在的联系，以达到模型的训练目的。这种方式使用了一定量的数据，但是由于需要实现人工的进行识别加标签这一过程，所以很费事。
无监督学习：现实生活中常常会有这样的问题：缺乏足够的先验知识，因此难以人工标注类别或进行人工类别标注的成本太高。很自然地，我们希望计算机能代我们完成这些工作，或至少提供一些帮助。根据类别未知(没有被标记)的训练样本解决模式识别中的各种问题，称之为无监督学习。这样模型就可以无差别的使用海量的数据而不需要人为的事先进行分类了。最典型最直接的应用：聚类。

1.Auto-Encoders

给定一个输入进行自编码，然后再解码，目标是使得解码生成的输入与输入尽可能一致。


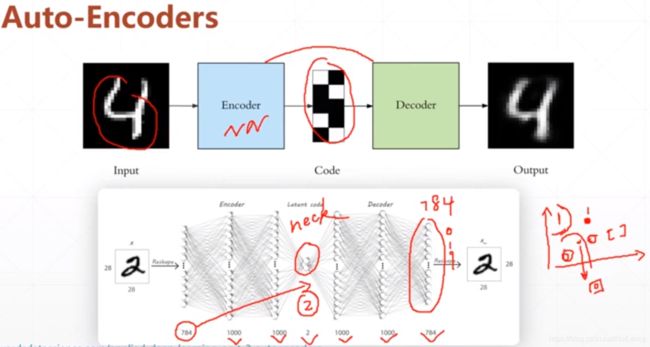
对于分类输入：是或不是，使用交叉熵loss函数求解梯度，然后BP。
对于回归输入：我们的loss function直接定义为原始数据和反向生成的数据两者之间的差距，然后求解梯度，进行BP。

1.降噪自动编码机（Denoising Autoencoder）

为了确保模型学习到的联系是更加高维的联系，而不是简单的例如像素的数值等信息，我们随机的对原始图片添加上噪声，然后再让模型进行还原。

2.Dropout AutoEncoders

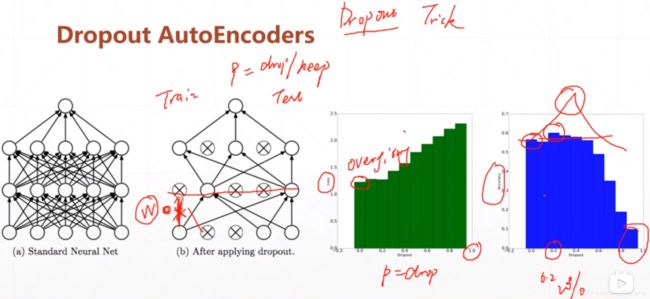
为了确保模型学习到的联系是更加高维的联系，而不是简单的例如像素的数值等信息，我们随机的断掉模型中的某些连接，然后再让模型进行还原。

3.对抗自编码器（Adversarial Autoencoders）

我们输入的数据x大多数都是服从于某种分布的，然而经过多轮epoch处理后，得到的z可能已经不再和x的分布相同了。所以需要

通过Discriminator的调节来尽可能的让AutoEncoders的处理结果服从某种设定的分布情况，一般设置为高斯分布。

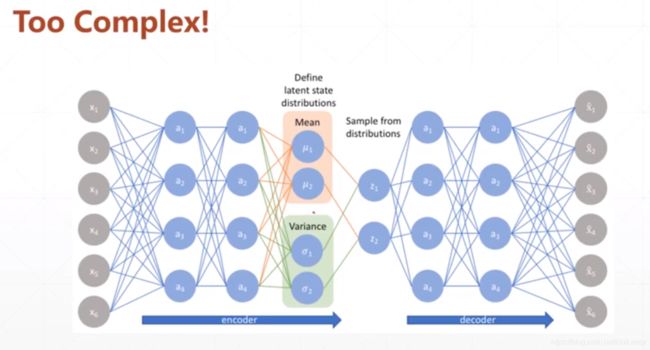
4.变分自编码器VAE(Variational Autoencoders)

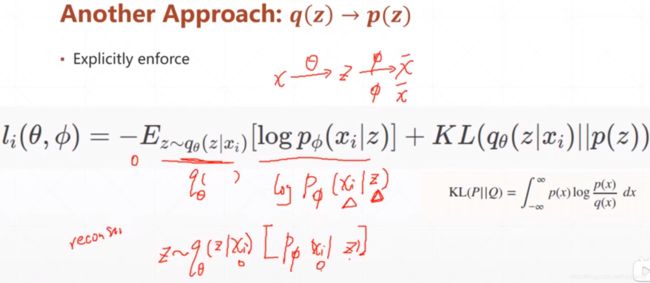
qθ(z|xi)表示在分布q下给一个xi得到z的概率，也就对应着xi通过网络θ得到对应的z，然后我们将数据z的分布情况sample出下一个网络的输入；p(z)表示给一个服从数据z分布的sample通过φ网络的处理得到x1的概率。所以KL(qθ(z|xi)||p(z))就表示着x和x1的差异。


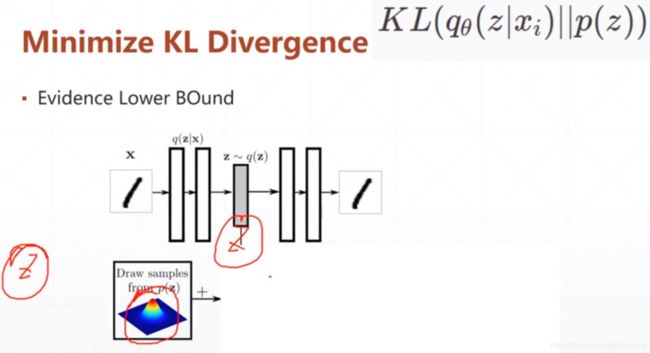
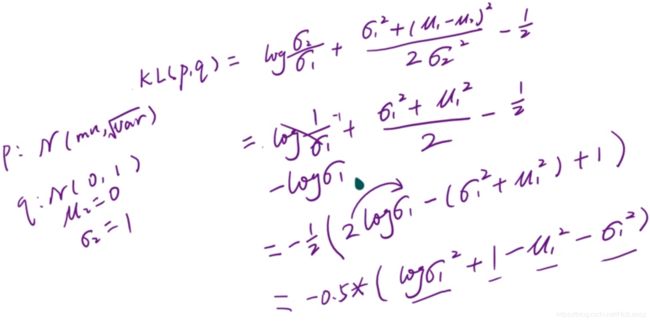
KL散度计算公式，让p分布尽可能的接近于q。
AutoEncoders的目的就是首先让数据x通过一个Encoder网络θ编码成一个服从于某种分布q的数据z，然后再通过Decoder网络φ解码成服从某种分布p的x1，而且尽可能的要让x和x1相同而且分布p和分布q也要尽可能的相似，也就是KL(q||p)散度尽可能的小。

5.总结

AutoEncoders就是通过Encoder降维来寻找大量数据x之间的共同性latent code，然后再通过Decoder升维来还原出与原来数据类似的东西x1，甚至可以通过调整前面降维找到的共同性的数值，来生成原本不存在的但与本来数据类似的东西x2。
了解一下各种loss函数的计算方法

rec_loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=x, logits=out)  # 为什么？如果不用这个loss函数的话效果很差

2.生成对抗网络（Generative Adversarial Networks，GAN）

p(x)表示x在其分布p下的概率，但是究竟是什么分布我们并不知道，而且我们想要使p(x)的概率尽可能的大，所以我们用一个复杂的神经网络g去模拟分布p，已达到我们给一个数据z经过神经网络g之后能使得我们的p(x) = p(x|z) * p(z) = 这一部分就相当于网神经网络里输入z最大。
而无监督学习VAE就是首先先通过原始数据x‘学习其中的数据分布情况p（也就是encoder网络做的事情）并且假设这个p实际是服从实际存在的某种分布（一般认为是正态分布），从而引入KL散度来使逼近与正态分布。然后我们在通过已知的数据分布情况p，sample解码网络的输入数据z，通过解码网络重新生成“原始数据x”，并且要使得真实的原始数据x‘和解码生成的“原始数据x”差异最小。

生成对抗网络GAN则是一个生成器通过输入随机数据生成Fake数据，然后再有一个判别器用来识别Fake数据属不属于Real数据，输出0或1。最终的结果是达到一个均衡——对于生成器生成的Fake数据，判别器有50%的概率识别成真实数据，也有50%的概率识别成虚假数据，这样我们就有了一个对于随意的输入都能生成一份较为真实的数据的数据生成器。

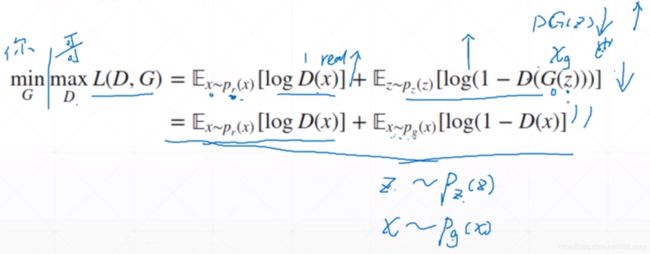
D代表判别器网络，G代表生成器网络。
对于判别器来说它的期望是最大化D网络的判错能力——真实数据都识别为1，生成器生成的数据都判别为0。所以他要maxL(D,G)=最大化D网络的对于真实数据的判真能力 + 最大化D网络的对于Fake数据的判假能力
对于生成器来说它的期望是最小化D网络的判错能力，所以他要minL(D,G)=最小化D网络的对于真实数据的判真能力 + 最小化D网络的对于Fake数据的判假能力（x~pg(x)表示x数据是经过G网络生成的Fake_x数据）。

分开研究判断网络D和生成网络G的最优情况：
首先固定G网络（也就相当于固定了通过G网络后数据的分布Pg(x)的数值）单独研究此时D网络所能达到的最优情况D^*(x)；
然后查看在D网络判断能力最强的情况下G网络的最优状况。
先将生成网络G的输入固定，单独训练判断网络D，研究D网络L(D,G)函数(类似于loss函数不过对于D网络来说是求其最大值)的构成及达到最大值时x的分布情况D^*(x)
首先将数学期望表示成积分形式：E(x) = 积分符号大S x * f(x) dx

为了研究G网络的最优情况，引进一个由KL散度构建生成的JS散度：
KL散度是不对称的，也就是说KL(q||p)和KL(p||q)不同的，JS散度是对称的。

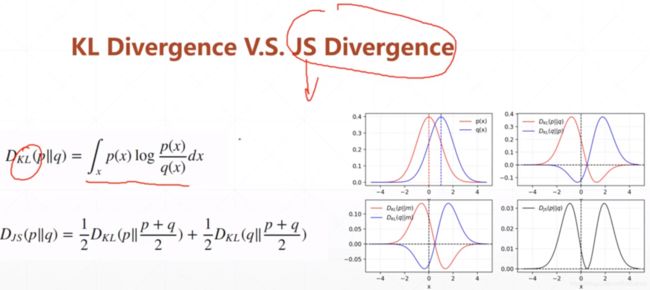
当生成网络D最优达到D^*时，我们解冻G网络的参数，研究此时G网络能到达的最优情况及loss函数的表达：

我们可以看到当在D网络达到最优的情况下G网络的loss函数L(G,D^*)表达为图中最下方的公式，Djs(Pr||Pg)散度的取值是(0, log2)的所以要想loss函数取最小值则Djs(Pr||Pg)散度的值就需要取得0，此时也就意味着Pr(Preal真实图片的数据分布情况)和Pg(经过G生成网络处理后的图片数据分布情况)完全一致。
此时我们再回看令D网络取得最优表现时的D^*(x)的表达式就会发现Pr(x) / Pr(x) + Pg(x) = 1 / 2（纳什均衡点)。

1.Deep Convolutional GAN, DCGAN

为了生成任意大小的图片，我们需要一种卷积来放大feature map——Transposed Convolution，转置卷积

效果对比GT(Ground Truth)GAN(GAN生成的图片)

GAN的缺陷：Training Stability

对GAN进行训练的一大目标就是使得生成的数据的分布p尽可能的与真实的数据q的分布相同，所以我们引入了KL散度和JS散度来衡量两个分布的差异，但是有一个问题是：在初始时分布p和q他们的差异会很大，大概率会出现几乎没有任何相互重叠的地方，所以我们需要快速的对生成网络进行调整，以便于训练。但问题就在于，由于KL散度和JS散度这两个度量分布差异的方法在两个分布没有任何相互重叠的时候，他们的值分别是正无穷和log2变成了一个常数，没有很好的量化，这就会出现梯度弥散现象，也就导致我们没有办法很根据梯度下降对网络进行调整。（loss函数的值是个常数，导数为0，没有很好的体现出一个变化的趋势，我们在梯度下降的时候也就不知道该往哪边下降了。）


所以我们重新引入了一个新的Wasserstein Distance来衡量两个分布的相似度，以解决KL和JS散度存在的问题。

Wasserstein Distance

Wasserstein Distance，我们将不同的分布图像视作一个个土堆，研究如何能够通过“移土”的方式将两个分布变得相同，然后将代价最小的“移土”方式视作两个分布的差异。


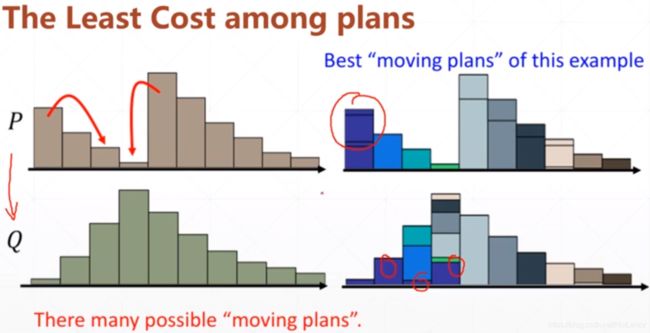
（我自己想的Wasserstein Distance计算方法是从左往右扫描，在没遇到比原来数组对应位置上多的位置时，多的搬到少的上面，优先放到最左侧的位置上，如果遇到了，记录下来位置，直到第一个数值多的位置与对照位置的数值相同后，从第二个数值多的位置上重新开始“移土”。可能不对，既是是对的应该也有更加巧妙的算法，我就暂时不去研究了。）
以上是离散的情况，实际问题几乎都是连续的：


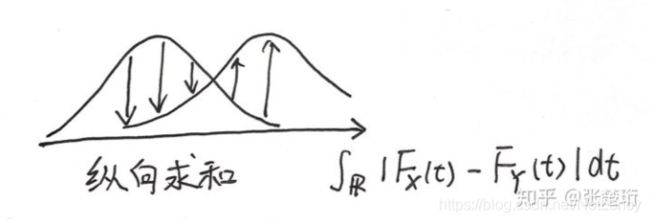
为了更好的解决梯度的不平缓问题，WGAN中引入了新的GradientPenalty机制，用来限制梯度在(0, 1)范围内。（说实话这个机制没太看明白）

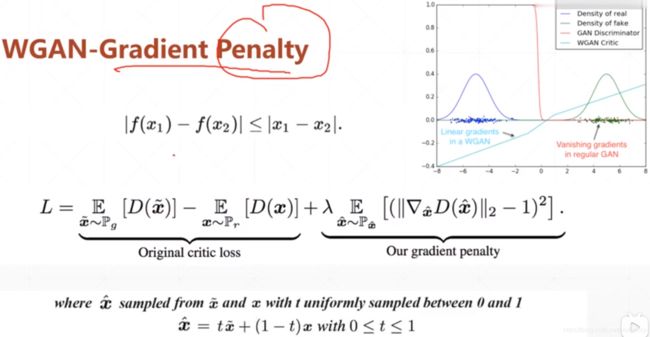
p150

11.

12.

待解决的问题：

1.什么样的任务要用什么样机器学习方法？什么样的网络？
2.网络的结构怎么搭建？用几层？每一层的参数又怎样设置？
3.用什么样的激活函数？不同的激活函数之间对训练的数据又有什么要求？应用中如何选择合适的激活函数？
这个问题目前没有确定的方法，凭一些经验吧。
1）深度学习往往需要大量时间来处理大量数据，模型的收敛速度是尤为重要的。所以，总体上来讲，训练深度学习网络尽量使用zero-centered数据 (可以经过数据预处理实现) 和zero-centered输出。所以要尽量选择输出具有zero-centered特点的激活函数以加快模型的收敛速度。
2）如果使用 ReLU，那么一定要小心设置 learning rate，而且要注意不要让网络出现很多 “dead” 神经元，如果这个问题不好解决，那么可以试试 Leaky ReLU、PReLU 或者 Maxout.
3）最好不要用 sigmoid，你可以试试 tanh，不过可以预期它的效果会比不上 ReLU 和 Maxout.
4.用不用Dropout？在哪里用？数值设多大？
答：0.2~0.4，是经验值。
5.用哪种优化器？各种优化器的不同点，与优点所在？学习率设置多少？动量参数又设置多少？
6.loss函数用哪一种？
7.模型的效果不好怎么办？过拟合？欠拟合？
8.什么是机器学习？
答：什么是机器学习，是找关系；可关系是什么呢？关系的建立基于什么呢？个人的理解，机器学习的本质，其实就是对人的经验的利用。这就意味着，你要想算法work，人的经验先应该基本上可以work，最起码这个问题可以用机器学习来解决；还有，人的经验利用，本质就是准确的列出可能的关联因素，加以分析确定主要因素，所以要想模型有用，你还得选出具有代表性的潜在features. 跑题说一下，深度学习的股票预测， 至今不能work，不是说深度模型不好，而是说，模型有了，你能把潜在因素包含进去吗？正所谓巧妇难为无米之炊，没有米，饭自然下不了。

对于supervised learning 和 semi-supervised learning, 之间把算法当作黑盒子，给它input和output，它建立模型告诉我们关联就可以；但是对于unsupervised learning, 问题就来了。我们没有这种明确的目的，要分类，我们也没有output labels. 最重要的是，我们不知道数据自身可不可具有一定的特征，从而借助这些特征把数据分类。根据我的machine learning使用经验，在不知道模型能不能建起来，performance好不好的之前，先问问自己，使用人的经验能不能把数据聚类。这就涉及到机器学习的本质了。

扯远了，那什么样的数据类型，能用unsupervised learning呢？总结上段文章的分析，1.这个数据要可以根据人的经验，能基本聚类，而不是看起来毫无章法。这谈的是feasibility。 2，含有潜在的pattern，不管它是implicit的被提到，还是explicit被提到，最起码包含一下具有区分度的pattern。这谈的是performance。

总而言之，无监督学习的本质就是，对于各种数据，我虽然不知道你讲的是什么，但是我知道你们讲的是相似的东西，还是不同的东西。实现好的performance的无监督学习，不仅仅是数据质量问题，而是遗忘问题，就是有效的忘掉一些不具有区分度的特征，记住有区分度的特征。

9.机器学习的三大主义？每种主义的代表？SVM、DL、KNN、决策树、集成学习、贝叶斯算法、聚类算法、Auto-Encoders、无监督学习？