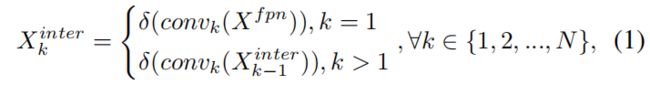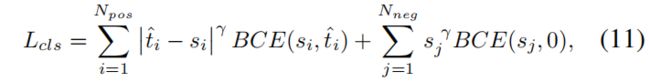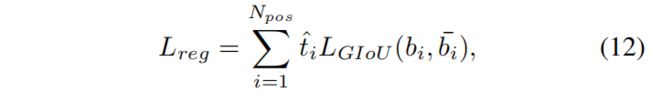TOOD: Task-aligned One-stage Object Detection 原理与代码解析

paper：TOOD: Task-aligned One-stage Object Detection

code：https://github.com/fcjian/TOOD 

存在的问题 

目标检测包括分类和定位两个子任务，分类任务学习的特征主要关注物体的关键或显著区域，而定位任务是为了精确定位整个对象主要关注物体的边界。由于分类和定位学习机制的不同，两个任务学习的特征的空间分布可能会不同，当使用两个独立的分支进行预测时，会导致一定程度的misalignment。如下图所示，Result栏第一行是ATSS预测dining table的结果，其中红色和绿色的patch分别是置信度最高和IoU最大的anchor，对应的预测bounding box分别是红色和绿色的box。可以看出，分类得分最高的anchor预测的bounding box和披萨的IoU更大，而和目标IoU最大的anchor分类得分却很低，反映出两个任务的misalignment。而第二行是TOOD的预测结果，可以看出分类得分最高的anchor同时也是IoU最大的。

本文的创新点

为了解决上述存在的问题，本文提出了一种任务对齐的单阶段目标检测模型TOOD（Task-aligned One-stage Object Detection），通过设计一种新的head和alignment-oriented学习方法，来更准确地对齐两个任务。具体如下

Task-aligned head. 与传统的单阶段目标检测模型中，分类和定位分别使用两个并行分支的结构不同，本文设计了一个任务对齐的head，以增强两个任务之间的交互，从而使它们的预测保持一致。T-head包括计算task-interactive特征，并通过新提出的Task-Aligned Predictor（TAP）进行预测，然后根据task alignment learning提供的信息对两个预测的空间分布进行对齐。

Task alignment learning. 为了进一步克服misalignment问题，作者提出了Task Alignment Learning（TAP）来拉近两个任务最优的anchor。这是通过设计了一个新的样本分配方法和任务对齐的损失函数来实现的，前者通过计算每个anchor的任务对齐程度来分配标签，后者在训练过程中逐步统一最适合两个任务的anchor。因此在推理阶段，一个分类得分最高的anchor同时也是定位精度最高的。

方法介绍

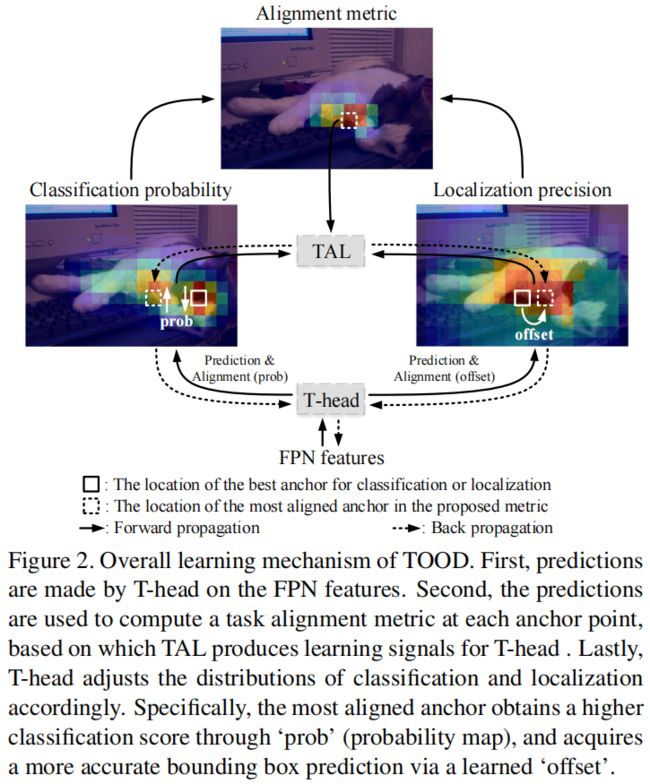
本文通过新设计的T-head和TAL来对齐两个子任务，如下图所示，两者可以协同工作以改进两个任务的对齐方式。具体来说，T-head首先对FPN特征的分类和定位进行预测，然后TAL计算一个对齐metric，这个指标用来衡量两个任务的对齐程度，最后T-head利用在反向传播过程中从TAL计算得到的对齐指标自动调整分类概率和定位预测。

Task-aligned Head

如上图所示，(a)是常见的one-stage detector的head结构，(b)是本文提出的T-head，它包括一个简单的特征提取器和两个TAP。为了增强分类和定位之间的interaction，本文使用特征提取器从多个卷积层中学习task-interactive特征，如(b)中间蓝色部分所示。\(X^{fpn} \in \mathbb{R}^H\times W\times C\) 是FPN特征，特征提取器使用 \(N\) 个连续的卷积层和激活函数来计算task-interactive特征，如下所示

其中 \(conv_{k}\) 是第 \(k\) 个卷积层，\(\delta\) 是 \(relu\) 函数。这样就用head中的单个分支从FPN特征中提取出了丰富的多尺度特征，接着这些交互特征被送进两个TAP进行分类和定位的对齐。

Task-aligned Predictor（TAP）

由于单一分支的设计，任务交互特征不可避免的会在两个不同任务之间引入一定程度的特征冲突，这是因为分类和定位的目标不同，因此专注于不同类型的特征，比如不同的层次和感受野。因此本文提出一种层注意力机制，通过在层级动态计算不同任务特定的特征从而进行任务分解。如图3(c)所示，对于分类和定位，分别计算其task-specific特征：

其中 \(\omega_{k}\) 是学习到的layer attention权重 \(\omega \in \mathbb{R}^{N}\) 的第 \(k\) 个元素。\(\omega\) 是根据cross-layer任务交互特征计算得到的，并且能够捕获层之间的交互关系：

其中 \(fc_{1}\) 和 \(fc_{2}\) 是两个全连接层。\(\sigma\) 是sigmoid激活函数，\(x^{inter}\) 是对 \(X^{inter}\) 应用average pooling得到的，而 \(X^{inter}\) 是对 \(X^{inter}_{k}\) 进行concatenate得到的。

最后，分类和定位的预测结果根据每个任务的 \(X^{task}\) 按下式计算得到：

其中 \(X^{task}\) 是对 \(X^{task}_{k}\) 进行concatenate得到的，\(conv1\) 是用于降维的1x1卷积，\(Z^{task}\) 经过 \(sigmoid\) 转换为分类得分 \(P\in \mathbb{R}^{H\times W\times 80}\)，经过 \(distance{\small -}to{\small -}bbox\) 转换得到定位预测 \(B\in \mathbb{R}^{H\times W\times 4}\)。

Prediction alignment.

在预测阶段，通过调整两个预测的空间分布进一步对齐两个任务。和之前使用centerness分支或IoU分支的模型不同，它们只能根据分类特征或定位特征对分类得分进行调整，而本文在用任务交互特征对齐两个预测时同时考虑到了两个任务。值得注意的是作者在两个任务上分别执行对齐方法，如上图(c)所示，作者使用了一个空间概率图 \(M\in \mathbb{R}^{H\times W\times 1}\) 来调整分类预测

其中 \(M\) 是从根据任务交互特征计算得到的，因此在每个空间位置都可以学习到两个任务的一致性。

同时为了对定位预测进行对齐，还从任务交互特征中学习了空间偏移图 \(O\in \mathbb{R}^{H\times W\times 8}\)，具体来说学习到的空间偏移量是最对齐的anchor能够识别周围的最佳边界预测：

其中索引 \((i,j,c)\) 表示一个tensor中通道 \(c\) 中 \((i,j)\) 位置。式(6)是通过双线性插值实现的，每个通道的偏移量都是独立学习的，这意味着每个对象的每个边界都有其自己学习到的偏移量，这就使得四个边界的预测更加准确，因为每个边界都可以从其附近最精确的anchor进行学习。

两个对齐特征图 \(M\) 和 \(O\) 的计算方式如下

其中 \(conv1\) 和 \(conv3\) 是两个用于降维的1x1卷积，\(M\) 和 \(O\) 的学习是通过接下来要介绍的Task Alignment Learning（TAL）进行的。

Task Alignment Learning

TAL和之前的方法有两点不同，首先，从任务对齐的角度看，它基于一个单独设计的度量指标动态的挑选高质量的anchor。其次，它同时考虑到了anchor的分配和权重。具体包括一个样本分配策略和一个专门为调整这两个任务而设计的新的损失函数。

Task-aligned Sample Assignment

为了应对NMS，一个训练示例的样本分配应该满足以下的准则：（1）一个well-aligned的anchor的分类和定位预测都应该很精确。（2）一个misaligned的anchor预测的分类得分应该低这样在NMS中才能被抑制。本文设计了一个anchor对齐度量指标，用来衡量anchor的任务对齐程度，并集成到样本分配和损失函数中，以动态的细化每个anchor的预测。

Anchor alignment metric.

分类得分以及预测的bounding box和gt之间的IoU分别表明了两个任务的预测质量，因此作者将两者结合到一起设计了一个新的对齐衡量指标，如下

其中 \(s\) 和 \(u\) 分别表示分类得分和IoU，\(\alpha\) 和 \(\beta\) 是权重系数用来控制两个任务对任务对齐衡量指标的影响大小。

Training sample alignment.

作者将任务对齐指标引入样本分配汇总，具体来说，对每个目标，选择 \(t\) 值最大的 \(m\) 个anchor作为正样本，其余的作为负样本。

Task-aligned Loss

Classification objective.

作者用 \(t\) 值替换正样本的二分类标签值1，但是作者发现当 \(\alpha\) 和 \(\beta\) 增大时，\(t\) 变得非常小从而导致网络无法收敛，因此采用了一个normalized的 \(t\) 即 \(\hat{t}\)，\(\hat{t}\) 的最大值等于和每个对象IoU的最大值。替换后的交叉熵loss如下

为了缓解样本不平衡问题，作者使用了focal loss，将其中对应的标签替换后，最终的分类loss如下

其中 \(j\) 表示 \(N_{neg}\) 负样本中的第 \(j\) 个anchor，\(\gamma\) 是权重参数。

Localization objective.

和分类一样，回归损失里也加入了 \(\hat{t}\) 来进行re-weight，改进后的GIoU loss如下

其中 \(b\) 和 \(\bar{b}\) 分别表示预测的bounding box和对应的gt box。

代码解析

假设batch_size=2，模型的输入shape=(2, 3, 300, 300)，backbone=ResNet-50，neck=FPN，FPN的输出为[(2,256,38,38),(2,256,19,19),(2,256,10,10),(2,256,5,5),(2,256,3,3)]，然后遍历FPN每个level的输出， 分别计算分类和定位的预测结果。接下来的tood head部分实现都在tood_head.py中，这里以第一层(2, 256, 38, 38)为例，首先按式(1)提取task-interactive特征，代码如下，其中self.inter_convs就是6个连续的conv3x3-GN-ReLU，最终得到 \(X_{k}^{inter}\)。

# extract task interactive features
inter_feats = []
for inter_conv in self.inter_convs:
    x = inter_conv(x)
    inter_feats.append(x)  
# [(2,256,38,38),(2,256,38,38),(2,256,38,38),(2,256,38,38),(2,256,38,38),(2,256,38,38)]

接着将 \(X_{k}^{inter}\) 拼接成 \(X^{inter}\)，再经过平均池化得到 \(x^{inter}\)，然后分别对分类和定位任务进行分解。对应式(2)-式(4)

feat = torch.cat(inter_feats, 1)  # X^{inter}_{k} -> X^{inter}, (2,1536,38,38),1536=256x6
# task decomposition
avg_feat = F.adaptive_avg_pool2d(feat, (1, 1))  # x^{inter}, (2,1536,1,1)
cls_feat = self.cls_decomp(feat, avg_feat)  # (2,256,38,38)
reg_feat = self.reg_decomp(feat, avg_feat)  # (2,256,38,38)

任务分解包括layer attention和降维，注意任务交互特征是6层卷积的输出，每层通道数为256，因此拼接后通道数为256x6=1536，但层注意力是每层共享一个权重，因此权重的shape为(2, 6, 1, 1)。

mmdet中的实现是先将注意力的权重矩阵和降维 \(conv1\) 的权重矩阵相乘，然后再对任务交互特征进行计算。在paddledetection中这两步是分开的tood_head.py，这里仿照paddle的实现将两部分开得到tmp_feat如下面代码中注释部分，最终结果是一致的，但注意torch.allclose中要设置atol=1e2，将结果打印出来发现小数后第四位就会有差异，这可能是框架底层实现的原因。

另外mmdet和paddle的实现中都没有式(4)中的 \(conv2\)。

class TaskDecomposition(nn.Module):
    """Task decomposition module in task-aligned predictor of TOOD.

    Args:
        feat_channels (int): Number of feature channels in TOOD head.
        stacked_convs (int): Number of conv layers in TOOD head.
        la_down_rate (int): Downsample rate of layer attention.
        conv_cfg (dict): Config dict for convolution layer.
        norm_cfg (dict): Config dict for normalization layer.
    """

    def __init__(self,
                 feat_channels,
                 stacked_convs,
                 la_down_rate=8,  # 48
                 conv_cfg=None,
                 norm_cfg=None):
        super(TaskDecomposition, self).__init__()
        self.feat_channels = feat_channels  # 256
        self.stacked_convs = stacked_convs  # 6
        self.in_channels = self.feat_channels * self.stacked_convs  # 256x6=1536
        self.norm_cfg = norm_cfg
        self.layer_attention = nn.Sequential(
            nn.Conv2d(self.in_channels, self.in_channels // la_down_rate, 1),  # 1536//48=32
            nn.ReLU(inplace=True),
            nn.Conv2d(
                self.in_channels // la_down_rate,  # 32
                self.stacked_convs,  # 6
                1,
                padding=0), nn.Sigmoid())

        self.reduction_conv = ConvModule(
            self.in_channels,
            self.feat_channels,
            1,
            stride=1,
            padding=0,
            conv_cfg=conv_cfg,
            norm_cfg=norm_cfg,
            bias=norm_cfg is None)

    def init_weights(self):
        for m in self.layer_attention.modules():
            if isinstance(m, nn.Conv2d):
                normal_init(m, std=0.001)
        normal_init(self.reduction_conv.conv, std=0.01)

    def forward(self, feat, avg_feat=None):  # (2,1536,38,38),(2,1536,1,1)
        b, c, h, w = feat.shape
        if avg_feat is None:
            avg_feat = F.adaptive_avg_pool2d(feat, (1, 1))
        weight = self.layer_attention(avg_feat)  # (2,6,1,1)


        # tmp_weight = weight.unsqueeze(-1)  # (2,6,1,1,1)
        # tmp_feat = feat.reshape(2, 6, 256, 38, 38)
        # tmp_feat = tmp_feat * tmp_weight  # (2,6,256,38,38)
        # # tmp_feat = tmp_feat.reshape(2, 1536, 38, 38)
        # tmp_feat = tmp_feat.flatten(1, 2)  # (2,1536,38,38)
        # tmp_feat = self.reduction_conv(tmp_feat)  # (2,256,38,38)


        # here we first compute the product between layer attention weight and
        # conv weight, and then compute the convolution between new conv weight
        # and feature map, in order to save memory and FLOPs.
        conv_weight = weight.reshape(
            b, 1, self.stacked_convs,
            1) * self.reduction_conv.conv.weight.reshape(
                1, self.feat_channels, self.stacked_convs, self.feat_channels)
        # (2,6,1,1)->(2,1,6,1) * (256,1536,1,1)->(1,256,6,256) = (2,256,6,256)
        conv_weight = conv_weight.reshape(b, self.feat_channels,
                                          self.in_channels)  # (2,256,1536)
        feat = feat.reshape(b, self.in_channels, h * w)  # (2,1536,1444)
        feat = torch.bmm(conv_weight, feat).reshape(b, self.feat_channels, h,
                                                    w)  # (2,256,1444)->(2,256,38,38)
        if self.norm_cfg is not None:
            feat = self.reduction_conv.norm(feat)
        feat = self.reduction_conv.activate(feat)  # ReLU(inplace=True), (2,256,38,38)
        # 好像少了式(4)中的conv2


        # t = torch.allclose(tmp_feat, feat, atol=1e-2)
        # print(tmp_feat[0][0][0])
        # print(feat[0][0][0])
        # print(t)
        # exit()

        return feat

接下来计算分类预测和分类的空间概率图，其中sigmoid_geometric_mean是将入参分别取sigmoid、相乘、开根，对应式（5）

# cls prediction and alignment
cls_logits = self.tood_cls(cls_feat)  # 没有sigmoid的P, (2,20,38,38)
cls_prob = self.cls_prob_module(feat)  # 没有sigmoid的M, (2,1,38,38)
cls_score = sigmoid_geometric_mean(cls_logits, cls_prob)  # P^{align}, (2,20,38,38)

接着计算定位预测和定位空间偏移图，其中deform_sampling是根据学习到的空间偏移图对定位预测进行调整，其中具体实现用的可分离卷积，和双线性插值是一样的。

# reg prediction and alignment
if self.anchor_type == 'anchor_free':
    reg_dist = scale(self.tood_reg(reg_feat).exp()).float()  # (2,4,38,38), 为什么要exp
    reg_dist = reg_dist.permute(0, 2, 3, 1).reshape(-1, 4)  # (2,4,38,38)->(2,38,38,4)->(2888,4)
    reg_bbox = distance2bbox(
        self.anchor_center(anchor) / stride[0],
        reg_dist).reshape(b, h, w, 4).permute(0, 3, 1,
                                              2)  # (2888,4)->(2,38,38,4)->(2,4,38,38)
reg_offset = self.reg_offset_module(feat)  # O, (2,8,38,38)
bbox_pred = self.deform_sampling(reg_bbox.contiguous(),
                                 reg_offset.contiguous())  # (2,4,38,38)

在对分类和定位预测结果进行调整后得到模型的最终预测，接下来就是正负样本分配和计算损失。在task_aligned_assigner.py中针对每个对象计算了 \(t\) 值并挑选 \(m\) 个 \(t\) 值最大的anchor作为正样本，其余作为负样本，代码如下，其中m=13

# select top-k bboxes as candidates for each gt
alignment_metrics = bbox_scores ** alpha * overlaps ** beta  # t
topk = min(self.topk, alignment_metrics.size(0))  # 13

在分配好正负样本后，就是计算损失函数，回到tood_head.py中，在函数_get_target_single()中计算每个anchor对应的分类标签和回归target，其中对 \(t\) 值normalized得到 \(\hat{t}\)，代码如下

pos_norm_alignment_metrics = pos_alignment_metrics / (
        pos_alignment_metrics.max() + 10e-8) * pos_ious.max()  # normalized t

注意，在mmdet的实现中，前4个epoch，标签分配用的是ATSS，topk=9，损失函数用的是Focal loss。之后标签分配改为本文提出的TaskAligned标签分配方法，topk=13，损失函数改为Qualiy Focal loss。定位损失全程是GIoU loss。

另外一些参数的选择，提取任务交互的连续卷积层个数 \(N=6\)，anchor对齐度量指标 \(t\) 中 \(\alpha=1,\beta=6\)，标签分配取 \(t\) 值最大的 \(m=13\) 个anchor作为正样本。

实验结果

下面是一些本文提出的T-head+TAL的测试图，以及和ATSS的对比，可以看出T-head+TAL可以很好的对齐两个预测，最终分类得分最高的预测同时也是IoU最大的。

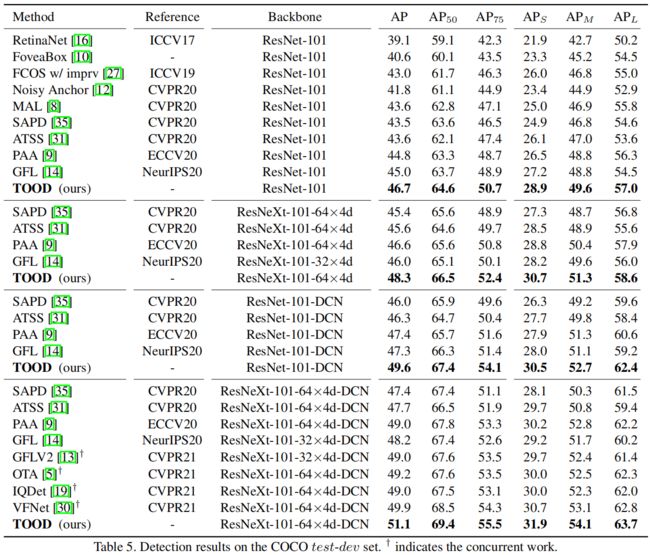
下面是和一些当前主流的单阶段检测模型以及标签分配方法的对比，TOOD取得了SOTA的结果。