【单目3D目标检测】MonoFlex论文精读与代码解析

Preface

Zhang Y, Lu J, Zhou J. Objects are different: Flexible monocular 3d object detection[C]. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021: 3289-3298.
Paper
Code

Abstract

现有单目3D目标检测大多忽略了对象之间的差异，对所有对象进行同等和联合处理可能会很难检测到严重截断的对象，并且这些硬样本会增加学习负担，并影响对一般对象的预测，造成检测性能下降。因此，统一的方法可能无法找到每个对象，也无法预测精确的3D位置。为此，作者提出了一种灵活的检测器，它考虑了对象之间的差异，并以自适应方式估计其3D位置
 

Contributions

• 发现针对截断类(outside object)的目标，从2D到3D映射过程，需要的偏移量的分布与非截断类目标(inside objects)的偏移量分布差别很大，因此要解耦这两类目标，分别进行学习，也就是关注到单目三维目标检测中考虑目标间差异的重要性，提出了截断目标预测的解耦方法
• 边缘融合模块（Edge Fusion）
• 几何深度+直接回归（M+1）
• 提出了一种新的目标深度估计公式，它利用不确定性灵活地组合独立的估计器估计对象深度，而不是对所有对象采用单一方法
   

Pipeline

Nonoflex框架以及检测思想是从CenterNet扩展而来的，CenterNet的核心思想是将目标作为一个点，即目标BBox的中心点，检测器采用关键点估计来找到中心点，并回归到其他目标属性，例如2D边界框、维度、方向、关键点和深度。最终深度估计是回归深度和根据估计的关键点和尺寸计算的深度的不确定性组合：

• 首先，CNN主干网络从单张图像中提取特征图作为多个预测头的输入，其中图像级定位涉及热图（Heatmap）和偏移量（Offsets）
• 之后边缘融合（Edge Fusion）模块用于解耦截断对象的特征学习和预测
• 同时自适应深度集合采用四种方法进行深度估计，并同时预测其不确定性，从而形成不确定性加权预测
   

Problem Definition

物体的3D检测包括估计其3D位置$(x,y,z)$、尺寸$(h,w,l)$和方向$\theta$。尺寸和方向可以直接从基于外观的线索推断出来，而3D位置则转换为投影的3D中心$x_c=(u_c,v_c)$和对象深度$z$：
$$\begin{array}{rl}& x=\frac{\left(u_c-c_u\right)z}{f}\\ & y=\frac{\left(v_c-c_v\right)z}{f}\end{array}$$
其中，$(c_u,c_v)$为主点（principle point），$f$为焦距（focal length）。3D位置转换为投影中心和对象深度的示意图如下所示：

 

Decoupled Representations of Objects

Inside & Outside Objects

现有的单目3D检测方法对每个对象使用统一表示$x_r$，即2D边界框$x_b$的中心点。计算偏移${\delta }_c=x_c-x_b$回归以导出投影的3D中心$x_c$。根据物体的投影3D中心在图像内部还是外部，我们将物体分为两组，内部对象（Inside Objects）和外部对象（Outside Objects）在从2D中心到投影3D中心过程中，呈现完全不同的偏移${\delta }_c$分布：

因此，作者将将内外对象的表示和偏移学习进行解耦：

• 对于投影的3D中心位于图像内部的对象，它们由$x_c$直接识别，此时的偏移误差如下，其中$S$为CNN下采样率：
  $${\delta }_{in}=\frac{x_c}{S}-\lfloor \frac{x_c}{S}\rfloor$$
• 为了解耦外部对象的表示，作者通过 图像边缘 和 从$x_b$到$x_c$的之间的交点$x_I$来识别外部对象，交点$x_I$比简单地将$x_b$或$x_c$夹持到边界更有物理意义：
  $${\delta }_{out}=\frac{x_c}{S}-\lfloor \frac{x_I}{S}\rfloor$$

 

Edge Fusion

• 尽管内部和外部对象的表示在输出特征的内部和边缘区域中解耦，但共享卷积核仍然难以处理空间变量预测。因此，作者提出了一个边缘融合模块来进一步解耦外部对象的特征学习和预测
• 如下图所示，模块首先提取特征图的四个边界，并将它们按顺时针顺序（图文不一致）连接成边缘特征向量，然后由两个1×1卷积层处理，以学习截断对象的独特特征。最后，将处理后的向量重新映射到四个边界并添加到输入特征图。当应用于热图预测时，边缘特征可以专门预测外部对象的边缘热图，从而不会混淆内部对象的定位。为了回归偏移，${\delta }_{in}$和${\delta }_{out}$之间的显著尺度差异可以通过边缘融合模块解决

 

Loss

作者采用L1 Loss回归${\delta }_{in}$，Log-Scale L1 Loss回归${\delta }_{out}$，因为它对极端异常值更加鲁棒，偏移损失计算为：
$$L_{off}=\{\begin{array}{l}\left|{\mathbf{\delta }}_{in}-{\mathbf{\delta }}_{in}^{\ast }\right|\text{ if inside }\\ \log \left(1+\left|{\mathbf{\delta }}_{out}-{\mathbf{\delta }}_{out}^{\ast }\right|\right)\text{otherwise}\end{array}$$
其中，${\delta }_{in}$和${\delta }_{out}$表示预测，${\delta }_{in}^{\ast }$和${\delta }_{out}^{\ast }$表示GT

 

Visual Properties Regression

视觉属性的回归，包括对象的2D边界框、尺寸、方向和关键点

2D Detection

作者不将对象表示为2D中心，遵循FCOS将代表点$x_r=(u_r,v_r)$的距离回归到2D边界框的四个侧面，其中代表点$x_b$表示内部对象，$x_I$表示外部对象。此外，2D检测采用GIOU损失，因为它对规模变化的鲁棒性
 

Dimension Estimation

考虑到每个类别中对象之间的小方差，本文回归了相对于统计平均值的相对变化而不是绝对值，对于每个类$c$，训练集的平均维数表示为$(h_c,w_c,l_c)$，那么尺寸回归的L1 loss表示为：
$$L_{dim}=\sum _{k\in \{h,w,l\}}\left|{\bar{k}}_c{e}^{{\delta }_k}-k^{\ast }\right|$$

Orientation Estimation

方向可以表示为相机坐标系中的全局方向或相对于观察方向的局部方向。对于位于$(x,y,z)$的对象，其全局方向$r_y$和局部方向$\alpha$满足：
$$r_y=\alpha +arctan(x/z)$$

• 具有相同全局方向但不同视角的对象将具有不同的局部方向和视觉外观。因此，我们选择使用MultiBin损失来估计局部方向，这将方向范围划分为无重叠区域，以便网络可以确定对象位于哪个区域，并估计区域中心的剩余旋转

 

Keypoint Estimation

为每个对象定义$N_k=10$个关键点，其中包括3D边界框的8个顶点$k_i,i=1\dots 8$、底部中心$k_9$和顶部中心$k_{10}$的投影：

在后续预测几何深度的时候，会利用到这十个顶点，来计算三类目标的2D高度，再根据投影公式来计算目标的深度
 

Adaptive Depth Ensemble

本文将对象深度的估计表述为 M + 1 个独立估计器的自适应集成，包括来自关键点的直接回归和 M 个几何深度

Depth From Keypoints

利用目标的2D高度和3D高度之间的相对比例来计算目标深度（即投影公式：$z_l=\frac{f\times H}{h_l}$），从高度求解深度不仅与orientation估计无关，而且受dimension估计误差的影响较小（预测时直接回归10个关键点，而计算targets中的10个关键点时则是需要利用labels中的目标三维坐标、偏航角以及长高宽）：

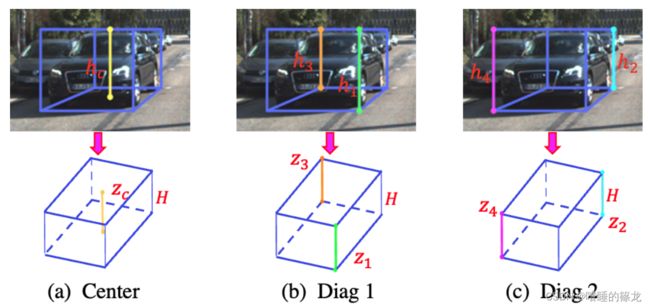
Uncertainty Guided Ensemble

利用M+1个深度估计值和不确定性，进行加权求解平均值：
$$z_{soft}=\left(\sum _{i=1}^{M+1}\frac{z_i}{{\sigma }_i}\right)/\left(\sum _{i=1}^{M+1}\frac{1}{{\sigma }_i}\right)$$
soft ensemble可以为那些更自信的估计器分配更多的权重，同时对潜在的不准确不确定性具有鲁棒性

 

Run Code

1、创建环境

# 创建conda虚拟环境：python==3.7, pytorch==1.4.0 and cuda==10.1
conda create -n monoflex python=3.7 -y
conda activate monoflex
pip install torch==1.4.0 torchvision==0.5.0

# clone代码
git clone https://github.com/zhangyp15/MonoFlex
cd monoflex
# 安装库文件
pip install -r requirements.txt

# Build DCNv2 and the project
cd model/backbone/DCNv2
. make.sh
cd ../../..
python setup.py build develop

2、准备数据集并修改路径

数据集下载及配置同SMOKE中的步骤。下载完成后，打开/monoflex/config/paths_catalog.py文件，修改数据集路径：

class DatasetCatalog():
    DATA_DIR = "/your_datasets_root/"
    DATASETS = {
        "kitti_train": {
            "root": "kitti/training/",
        },
        "kitti_test": {
            "root": "kitti/testing/",
        },

    }

3、修改训练及测试参数
打开/home/rrl/det3d/monoflex/runs/monoflex.yaml文件，按照需要进行修改：

SOLVER:
  OPTIMIZER: 'adamw'
  BASE_LR: 3e-4
  WEIGHT_DECAY: 1e-5
  LR_WARMUP: False
  WARMUP_STEPS: 2000

  # for 1 GPU
  LR_DECAY: 0.1
  # 使用epoch作为训练的次数，而不是iterations
  EVAL_AND_SAVE_EPOCH: True
  EVAL_EPOCH_INTERVAL: 1
  SAVE_CHECKPOINT_EPOCH_INTERVAL: 2
  # 训练epoch数
  MAX_EPOCHS: 100
  DECAY_EPOCH_STEPS: [80, 90]
  # batchsize大小
  IMS_PER_BATCH: 8
  EVAL_INTERVAL: 1000

TEST:
  UNCERTAINTY_AS_CONFIDENCE: True
  # 检测阈值越大，检测出来的框越少
  DETECTIONS_THRESHOLD: 0.9
  METRIC: ['R40']
# 保存路径
OUTPUT_DIR: "./output/exp1"

4、开始训练

• 单GPU训练

CUDA_VISIBLE_DEVICES=0 python tools/plain_train_net.py --batch_size 8 --config runs/monoflex.yaml --output output/exp

• 第一次训练，会自动下载预训练权重dla34-ba72cf86.pth，因为要，所以下载很慢，大家可以从这里直接下载到本地，然后上传到/root/.cache/torch/checkpoints/dla34-ba72cf86.pth即可

5、测试及可视化

CUDA_VISIBLE_DEVICES=0 python tools/plain_train_net.py --config runs/monoflex.yaml --ckpt YOUR_CKPT  --eval --vis

可视化结果如下：

6、保存可视化图像（可选）
为了实时保存可视化图像，对源代码进行以下修改：

• 打开/monoflex/engine/inference.py文件，在inference函数中调用compute_on_dataset函数的地方，添加新的传参output_dir = output_folder，也就是把保存路径传给之后的可视化函数，目的是将可视化结果保存在我们指定的目录下：

• 打开/monoflex/engine/inference.py文件，在compute_on_dataset函数中添加新的传参output_dir = None，并且设置新的子文件夹save_jpg，将作为参数其传递给
  show_image_with_boxes函数：

• 打开/monoflex/engine/visualize_infer.py文件，在show_image_with_boxes函数中添加新的传参save_dir = None，

• 最后，在show_image_with_boxes函数的最后，添加保存图像的代码，这里既保存plt.fifure()合成的完整图像（包括热力图、检测结果图和BEV视角正确和错误的推理图），又保存检测结果图（即img3）：

最终可视化过程中，实时保存图像的目录如下所示：

Reference

【单目3D检测】Monoflex论文阅读

文献阅读：(CVPR2021)Objects are Different: Flexible Monocular 3D Object Detection