基于量子计算的无收益标的资产欧式看涨期权定价和delta风险分析

本文的目标是验证量子计算可应用于金融衍生品的定价和风险分析，场景选择为最简单的无收益标的资产欧式看涨期权的定价和delta风险参数的计算，场景可以用数值方法和经典蒙特卡洛算法求解，以做相互对照。

1. 问题

1.1. 描述

已知一个以无收益标的资产为目标的欧式看涨期权合约（European Call Options），即，已知合约的标的资产期初价格（记作S0）、执行价格（Strike Price，记作K）、生效时间到到期日之间的时间长度（以年为单位，记作T），求在给定时间点（本文中为期权生效的日期），合约的价格（因为是欧式（European）看涨（Call）期权的，所以记作CE）和风险参数（本文只计算Δ，记作delta）。

1.2. 解读

期权是一种合约，赋予持有人在到期日或该日之前任何时间以执行价格买入或卖出标的资产的权利。只能在到期日行权的就是欧式期权。在到期日行使的是买入权力的就是欧式看涨期权。期权的标的资产不会产生任何收益（如利息、分红等）的就是无收益标的资产。期权的payoff就是行权时带来的收益或损失，即，行权时标的资产价格（记作ST）与执行价格的差。期权的定价也就是payoff的数学期望（即所有可能的值乘以其概率后加和）。期权有一堆用希腊字母代表的风险参数，本文中选取delta，它反映的是期权定价对标的资产期初价格的敏感程度，在下面要用的BSM模型里，delta就是期权定价相对于标的资产价格的一阶偏导数，其实就是行权时的标的资产价格大于等于执行价格的概率。

综上，问题就是已知S0、K、T，求CE、delta。

2. 原理

解决上述问题的量子算法（量子蒙特卡洛算法）包括以下4步：

1. 基于BSM模型算出标的资产到期日价格ST的取样。制作初始化量子线路，线路的作用是将样本及对应概率存进一组量子比特。
2. 制作payoff计算量子线路，线路的作用是针对上步的ST样本，计算其payoff。
3. 用量子振幅估计算法，将存在量子比特的振幅中payoff，也就是期权的定价提取出来。由于量子比特每次测量后就变化了（想象薛定谔的猫，就是猫装在盒子里，如果不看它，它就是“亦生亦死”，但每看它一次就从“亦生亦死”变成了“生”或者“死”），所以振幅估计的过程会多次调用上两步中的两个量子线路，最终按每次测量的结果的概率分布得出结论。
4. 制作delta计算量子线路，线路的作用是针对上步的ST样本，计算其delta。
5. 用量子振幅估计算法，将存在量子比特的振幅中delta提取出来，这次的振幅估计会多次调用第1、4步中的量子线路。
   以下内容为上述算法中涉及到的金融和量子计算基本原理：

2.1. BSM模型

BSM模型用于在任一时刻预计标的资产到期日价格：ST = S0 * e^(vol * WT + (r - 0.5 *vol^2) * t)

• ST：在当前时刻预计的标的资产到期日价格
• S0：标的资产期初价格
• e：自然常数，即，2.71828183…
• vol：波动率
• WT：符合正态分布的随机值，该正态分布的两个参数为0和T，T是生效时间到到期日之间的时间长度（以年为单位）
• r：无风险收益率
• t：当前时刻到到期日之间的时长（以年为单位）

对此公式两侧取e为底的对数，则得到：ln(ST) = vol * WT + ln(S0) + (r - 0.5 * vol^2) * t。因为WT符合正态分布（0,T），所以ln(ST)符合对数正态分布，以正态分布之间的转化公式，这个对数正态分布的两个参数mu和sigma如下：

• mu = ln(S0) + (r - 0.5 * vol^2) * t
• sigma = vol * √T

进而，依对数正态分布计算公式，此对数正态分布的数学期望mean、方差（所有可能的值与数学期望的差的平方和）variance和标准差（方差的平方根）stddev为：

• mean = e^(mu + 0.5 * sigma^2)
• variance = (e^(`sigma`2) - 1) * e^(2 * mu + sigma^2)
• stddev = √variance

2.2. 经典蒙特卡洛算法

经典蒙特卡洛算法解决期权定价问题，就是将2.1节中的WT按照符合正态分布的规律，反复随机生成，将所有算出的ST取均值，就得到了标的资产到期日价格，减去执行价格K，就是期权的定价了。

2.3. 量子蒙特卡洛算法

与经典蒙特卡洛算法不同的是，量子蒙特卡洛算法用2.1中算出的ST的数学期望mean和标准差stddev，生成ST的取值区间，即，数学期望左右各3倍标准差的区间，然后在此区间上直接为ST等步长取样，样本数量为2 ^ n，n为存储样本的量子比特的个数。这些样本符合对数正态分布，因此是可以计算出每个样本的出现概率的。这时，就可以将样本值对应到n个量子比特所代表2^n个数字上，并将所有概率作为这些数字的振幅存进这组量子比特。

接下来，再对这组量子比特施加量子计算，算每个ST样本的payoff值，这其实是个很简单的分段线性函数，即，ST<K时，结果是0，ST>=K时，结果是ST - K。但量子计算机的原理与传统计算机不同，它对分段线性函数的实现并不是直观，它是在原始量子比特组上增加了多个辅助量子比特，然后构建一个量子线路，线路作用于所有这些量子比特，数学上可以理解为是构建了一个特定的矩阵，乘在了所有量子比特代表的向量构成的矩阵上，本章后面的节会讲述基本原理，但就像我们只了解传统计算机的基本原理（0，1和加法器）以及上层高级编程语言代表的算法一样，我们也不会在每次运用量子算法时，将从量子力学到最终量子算法的实现过程都推到一遍。这个实现分段线性函数的量子线路，会将以特定精度估计的payoff的数学期望存储在一个辅助比特的振幅里。事实上，这时我们已经得到了想要的期权定价，只是我们无法将它读出来，如果直接测量，我们需要无数次的测量（每次测量都是至少一次矩阵预算），才能知道振幅所代表的概率，这样就得不偿失了。

所以，我们用量子振幅估计算法来提取这个辅助量子比特的振幅，振幅估计算法是几乎所有量子算法应用场景的最后一步，因为我们需要把数字从量子世界取回到传统计算机世界来，也许有一天量子计算机能直接下达操作指令时，它就不需要把藏在量子的振幅的信息吐出来了。

2.4. 量子、量子计算和量子算法

量子是组成万物的、不能再分割的组成部分，具备叠加性、一测量就坍缩等特性，量子计算主要就是在用这两个特性。这里只从实用角度出发解释量子计算里用到的量子比特，而不做量子力学和数学的推演。由于量子的叠加特性，与传统计算机的1个比特只能存储0或1相比，1个量子比特可以同时存储0和1，也就是说n个量子比特，可以同时存储2 ^ n个值，并且同时对他们进行运算。只要只在量子计算机里运转，无论如何运算，这些量子比特都同时保存着这些信息，但，一旦我们希望看到这些信息，也就是说只要我们一测量，这些量子比特就会坍缩到一个特定的值。具体坍缩到哪个值，是有概率的，这个概率也存储在量子比特里，成为振幅。也就是说，n个量子比特，可以同时存2^n个数字，并且还为每个数字存了一个概率，如果我们测量的次数足够多，坍缩出来的结果就会按照这个概率分布。

现在的大多数量子计算机，就是用这个思路，将数据从振幅到量子比特代表的值来回折腾，在数学模型上，就是一堆在复数域上的矩阵运算，在硬件实现上，也跟传统计算机类似，在作用到比特上的一堆逻辑门，但传统计算的门代表的就是折腾0和1，但量子计算机的逻辑门是现在矩阵运算。一堆矩阵运算放在一起，就构成了一个量子算法，对应的，一堆逻辑门放在一起，就构成一个量子线路。2.3中提到的将对数正态分布存到量子比特中、算payoff的分段线性函数、振幅估计分别对应这3套不同的矩阵运算及对应的量子线路。

振幅估计是其中需要解释一下的部分。振幅估计是结合相位估计和振幅放大两个算法，将存储在量子比特里的振幅的信息测量出来的算法。

相位估计是计算一个矩阵的复数特征值e^(2 * pai * i * theta)（其中e为自然常熟、pai为圆周率、i为虚数单位、theta为相位）里的相位theta的，需要用到量子傅里叶逆变换，传统傅里叶变换是将时域和频域信号进行转换，但量子傅里叶变换只是有跟传统傅里叶变换相同的数学形式，并没有对应的意义，相位估计使用量子傅里叶逆变换，只是为了将相位信息从振幅中转化到量子比例存储的值里，从而通过测量得到它。在做量子傅里叶逆变换前，相位估计需要执行一个量子线路（即一组矩阵运算），构建出符合量子傅里叶变换结果形式的表达式。振幅放大是通过构建特定的量子线路（也就是一组矩阵运算），使量子比特里存储的某个值的振幅尽量接近于1，这样一测量就一定会测量到这个值。振幅估计，就是将相位估计需要的那组矩阵运算，用振幅放大里的这组矩阵运算替代，这样能使最终的测量算法的复杂度极度降低。

振幅估计折腾来折腾去就是为了降低测量算法的复杂度，这是因为虽然量子计算很快，但是测量是个算法复杂度很高的动作。测量的目的是得出每个值及其对应概率，测量其实也是对量子比特组做矩阵运算，对于n个量子比特进行测量，就有2^n种矩阵运算，而且还要把每种矩阵运算运行多次，以得出概率。因为一旦测量，量子态就被破坏了，所以每测一次，又要把前面生成当前状态的算法重新跑一遍，这样就得不偿失，还不如用传统计算机了。所以，振幅估计这类的算法是量子算法能应用的前提条件。

如果想对量子算法有更直观的理解，可以到本源量子的量子云上去试试，这个量子云平台和IBM开源从操作方式，到应用场景资料都很像，本源的部分材料就是直接翻译的IBM开源平台的文档，可以省了看英文文档的麻烦。这种操作方式，让我想起了大学时学汇编语言时画的图，本质上，也确实是这么个对应关系。

在我们使用量子算法解决具体问题时，必须记住量子的奇怪特性，但又不能纠结于想要每次都推导出完整的量子运算过程，否则可能会疯掉。

2.5. 量子算法在金融行业的应用情况

现在国内外的科技大厂和创业公司都有不少在搞量子计算的落地和应用，海外的IBM、谷歌、微软，国内的百度、阿里、腾讯，美股已经有三家上市公司，国内也有几家创业公司融了多轮了，比如2.4里提到的本源量子。在金融行业应用上，国外的高盛、JP、富国等银行都在两三年前就开始了衍生品定价和风控的实践，从论文上看，再有两三年，就会有成熟的实际业务应用。国内建行（建信金科）与本源量子合作，也在今年上半年发表了在金融衍生品定价和风控领域的尝试。

2.6. 开源量子计算开发包Qiskit

如果说前面说到的本源量子云平台的操作界面对应着汇编语言，那量子计算开发包就是高级语言，Qiskit是IBM开源的量子计算开发包，当然每个量子计算平台都有自己的开发包（本源也有），作用就是屏蔽量子量子比特逻辑门的操作细节，提供常见的量子算法（即一堆矩阵运算）实现。因为Qiskit的资料完备，成熟度高，所以本文的验证基于Qiskit用python实现。在使用前，需要安装Qiskit的包：

pip install qiskit
pip install qiskit[visualization]
pip install qiskit[finance]

2.7. 开发工具Jupyter Lab

计算类程序都有参数调整，并实时看到效果的需求，所以建议用Jupyter Lab进行开发，Jupyter Lab就是Jupyter notebook的升级版，就是把Jupyter notebook里加上了能打开OS命令行窗口、Python的console等的命令，用如下命令安装：

pip install jupyterlab

然后，创建个工作路径，在OS命令行里进入工作路径，执行：

jupyter lab

在弹出的浏览器的Jupyter Lab页面里，把第3章的代码放进去就可以愉快的玩耍了。

3. 代码

以下代码验证使用量子虚拟机，即在传统计算机上模拟量子线路的执行。上文中可体验手感的本源量子云虽然也实现了期权计算器等场景，但其SDK不能免费使用，且其云平台也很不稳定，所以还是使用了Qiskit在量子虚拟机上验证。即使只是在量子虚拟机运行，因为其算法思路与传统蒙特卡洛不同，从风控角度，仍能作为与传统蒙特卡洛相互印证的输入。

import matplotlib.pyplot as plt
# 仅对Jupyter notebook生效的代码，以将绘制的图形直接显示出来
%matplotlib inline
import numpy as np

from qiskit import Aer, QuantumCircuit
from qiskit.utils import QuantumInstance
from qiskit.algorithms import IterativeAmplitudeEstimation, EstimationProblem
from qiskit.circuit.library import LinearAmplitudeFunction
from qiskit_finance.circuit.library import LogNormalDistribution

# 设置存储标的资产到期日价格ST样本的量子比特数量为3，即，取2^3=8个样本
num_uncertainty_qubits = 3

# 基于BSM模型，计算ST需要的参数
S0 = 7.1271  # 标的资产期初价格
vol = 0.04893752407882 # 波动率
r = 0.020703023955912545  # 无风险收益率
T = 94 / 365  # 期权合约的期限，94天，以年为单位

# 根据数学公式，计算ST的数学期望和标准差
# 计算ST的对数正态分布的参数mu
mu = (r - 0.5 * vol**2) * T + np.log(S)
# 计算ST的对数正态分布的参数sigma
sigma = vol * np.sqrt(T)
# 计算ST的数学期望
mean = np.exp(mu + sigma**2 / 2)
# 计算ST的方差
variance = (np.exp(sigma**2) - 1) * np.exp(2 * mu + sigma**2)
# 计算ST的标准差
stddev = np.sqrt(variance)

# 计算ST取样的区间的下限
low = np.maximum(0, mean - 3 * stddev)
# 计算ST取样的区间的上限
high = mean + 3 * stddev

print("标的资产到期日价格ST取样区间：[%f,%f]" % (low, high))

标的资产到期日价格ST取样区间：[6.046319,7.019962]

# LogNormalDistribution会构建一个量子线路（就是一堆矩阵运算），它作用于3个初始状态（初始状态为100%概率测量为0）的量子比特，使其存储8个在指定区间均匀取得的对数正态分布的变量的样本，及对应概率
# 参数num_uncertainty_qubits为被施加运算的量子比特的数量
# 参数mu为构建的对数正态分布的第一个参数，参数sigma^2为对数正态分布的第二个参数，这两个参数用于根据数学公式计算样本对应的概率
# 参数(low, high)为样本取值的区间
uncertainty_model = LogNormalDistribution(
    num_uncertainty_qubits, mu=mu, sigma=sigma**2, bounds=(low, high)
)
print("标的资产到期日价格ST的样本：     %s" % uncertainty_model.values)
print("标的资产到期日价格ST的样本的概率：%s" % uncertainty_model.probabilities)
print("该量子线路的线路图：")
print(uncertainty_model)

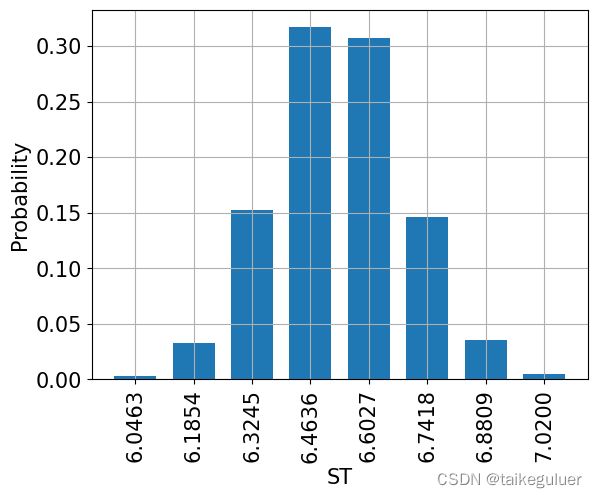
标的资产到期日价格ST的样本：     [6.04631886 6.1854107  6.32450254 6.46359438 6.60268621 6.74177805
 6.88086989 7.01996173]
标的资产到期日价格ST的样本的概率：[0.00297419 0.03285524 0.15291801 0.31684201 0.30748391 0.14648391
 0.03577825 0.00466448]
该量子线路的线路图：
     ┌───────┐
q_0: ┤0      ├
     │       │
q_1: ┤1 P(X) ├
     │       │
q_2: ┤2      ├
     └───────┘

# 绘制ST的分布情况
x = uncertainty_model.values
y = uncertainty_model.probabilities
plt.bar(x, y, width=0.1)
plt.xticks(x, size=15, rotation=90)
plt.yticks(size=15)
plt.grid()
plt.xlabel("ST", size=15)
plt.ylabel("Probability", size=15)
plt.show()

# 设置期权的执行价格，因为它需要在ST的取样区间内对验证才有意义，所以到这里再设置，实际情况执行价格肯定是预先确定的
strike_price = 6.4999

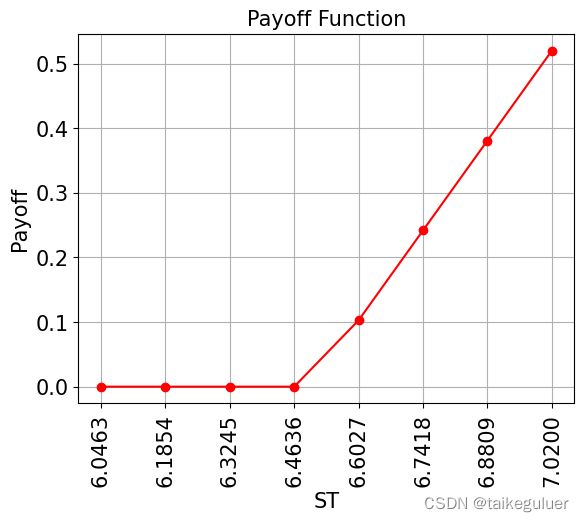
# 绘制用ST计算payoff的分段线性函数
x = uncertainty_model.values
y = np.maximum(0, x - strike_price)
plt.plot(x, y, "ro-")
plt.grid()
plt.title("Payoff Function", size=15)
plt.xlabel("ST", size=15)
plt.ylabel("Payoff", size=15)
plt.xticks(x, size=15, rotation=90)
plt.yticks(size=15)
plt.show()

# 直接计算出期权的定价和delta风险参数，用于对比后继量子算法计算出的结果的准确度
exact_value = np.dot(uncertainty_model.probabilities, y) # 计算payoff的数学期望，即将每个值与对应概率相乘后，求和
exact_delta = sum(uncertainty_model.probabilities[x >= strike_price]) # 计算delta风险参数，按它就是标志资产到期日价格大于执行价格的概率之和计算
print("期权的定价（payoff数学期望）:\t%.4f" % exact_value)
print("期权delta风险参数:          \t%.4f" % exact_delta)

期权的定价（payoff数学期望）:	0.0831
期权delta风险参数:          	0.4944

# 设置计算payoff的分段线性函数对应的量子线路需要的估算精度
c_approx = 0.25

# 创建计算payoff的分段线性函数的量子线路
breakpoints = [low, strike_price] # 分段函数自变量的第一段，标的资产到期日价格小于执行价格时，payoff永远为0
slopes = [0, 1] # 分段线性函数的各段斜率，第一段是0，第二段是1，第二段是1跟量子线路的具体实现有关，在第二段自变量和因变量是一一对应的
offsets = [0, 0] # 分段线性函数的各段位移，两段都是0，第二段是0跟量子线路的具体实现有关，在第二段自变量和因变量是一一对应的
f_min = 0 # 分段线性函数的因变量的取值下限
f_max = high - strike_price # 分段线性函数的因变量的取值上限，标的资产到期日价格大于执行价格时，payoff最大就是标的资产到期日价格与执行价格的差
# LinearAmplitudeFunction会根据输入的参数构建出量子线路，这个量子线路需要的量子比特包括存储样本的量子比特，但还需要增加辅助的量子比特
european_call_objective = LinearAmplitudeFunction(
    num_uncertainty_qubits,
    slopes,
    offsets,
    domain=(low, high),
    image=(f_min, f_max),
    breakpoints=breakpoints,
    rescaling_factor=c_approx,
)

# 结合初始化样本的量子线路和计算payoff的量子线路，构建一个量子线路，就是把着两堆矩阵运算放一起连续算，这个新的量子线路就是振幅估计算法的初始化线路
# 新的量子线路的量子比特数跟payoff计算量子线路的比特数量相等，为7
num_qubits = european_call_objective.num_qubits
european_call = QuantumCircuit(num_qubits)
european_call.append(uncertainty_model, range(num_uncertainty_qubits))
european_call.append(european_call_objective, range(num_qubits))
# 绘制这个新的量子线路
european_call.draw()

     ┌───────┐┌────┐
q_0: ┤0      ├┤0   ├
     │       ││    │
q_1: ┤1 P(X) ├┤1   ├
     │       ││    │
q_2: ┤2      ├┤2   ├
     └───────┘│    │
q_3: ─────────┤3 F ├
              │    │
q_4: ─────────┤4   ├
              │    │
q_5: ─────────┤5   ├
              │    │
q_6: ─────────┤6   ├
              └────┘

# 创建一个量子虚拟机实例（在传统计算机里模拟），用于基于运行上面构建的量子线路的振幅估计算法
qi = QuantumInstance(Aer.get_backend("aer_simulator"), shots=100)
# 创建一个振幅估计问题
# 参数state_preparation为振幅估计的状态初始化量子线路，即前文构建的量子线路，包含ST采样和payoff计算
# 参数objective_qubits标识振幅估计进行测量的目标比特列表，即上面7个量子比特里的q_3
# 参数post_processing指定测出振幅后的操作，它使用的LinearAmplitudeFunction的post_processing，这个操作会将估计出的振幅映射回原来的payoff值
problem = EstimationProblem(
    state_preparation=european_call,
    objective_qubits=[3],
    post_processing=european_call_objective.post_processing,
)
# 设置振幅估计需要的精度参数
epsilon = 0.01
alpha = 0.05
# 构建一个振幅估计IterativeAmplitudeEstimation（还有其他种类的振幅估计器，不同种类的实现逻辑和算法复杂度不同）
ae = IterativeAmplitudeEstimation(epsilon, alpha=alpha, quantum_instance=qi)
# 启动振幅估计器，即重复执行量子线路并进行测量
result = ae.estimate(problem)
# 从结果中取出期权定价的在95%（1-alpha）概率下的置信区间
old_conf_int = np.array(result.confidence_interval_processed)
old_result = result.estimation_processed

print("期权定价数值解：           \t%.4f" % exact_value)
print("期权定价量子算法解：       \t%.4f" % old_result)
print("期权定价95%%概率置信区间： \t[%.4f, %.4f]" % tuple(old_conf_int))

期权定价数值解：           	0.0831
期权定价量子算法解：       	0.0856
期权定价95%概率置信区间： 	[0.0820, 0.0893]

# 以上量子线路构建过程仅为展示算法逻辑，其实Qiskit中内置了无收益标的资产的欧式看涨期权的定价和风险参数的实现，直接调用如下即可：
from qiskit_finance.applications.estimation import EuropeanCallPricing

# 参数num_state_qubits是存储样本用的量子比特数
# 参数strike_price是执行价格
# 参数rescaling_factor是payoff计算分段线性函数线路的估算精度
# 参数bounds是ST的取样区间
# 参数uncertainty_model是ST的取样量子线路
european_call_pricing = EuropeanCallPricing(
    num_state_qubits=num_uncertainty_qubits,
    strike_price=strike_price,
    rescaling_factor=c_approx,
    bounds=(low, high),
    uncertainty_model=uncertainty_model,
)
# 设置振幅估计需要的精度参数
epsilon = 0.01
alpha = 0.05
# 创建一个量子虚拟机实例（在传统计算机里模拟）
qi = QuantumInstance(Aer.get_backend("aer_simulator"), shots=100)
# 从内置的欧式看涨期权的定价实现中取出需要振幅估计的问题
problem = european_call_pricing.to_estimation_problem()
# 构建一个振幅估计IterativeAmplitudeEstimation
ae = IterativeAmplitudeEstimation(epsilon, alpha=alpha, quantum_instance=qi)
# 启动振幅估计器，即重复执行量子线路并进行测量
result = ae.estimate(problem)
# 从结果中取出期权定价在95%（1-alpha）概率下的置信区间
conf_int = np.array(result.confidence_interval_processed)


print("期权定价数值解：                        \t%.4f" % exact_value)
print("自构建线路期权定价量子算法解：           \t%.4f" % old_result)
print("自构建线路期权定价95%%概率置信区间：     \t[%.4f, %.4f]" % tuple(old_conf_int))
print("Qiskit内置算法期权定价量子算法解：       \t%.4f" % (european_call_pricing.interpret(result)))
print("Qiskit内置算法期权定价95%%概率置信区间： \t[%.4f, %.4f]" % tuple(conf_int))

期权定价数值解：                        	0.0831
自构建线路期权定价量子算法解：           	0.0856
自构建线路期权定价95%概率置信区间：     	[0.0820, 0.0893]
Qiskit内置算法期权定价量子算法解：       	0.0878
Qiskit内置算法期权定价95%概率置信区间： 	[0.0840, 0.0916]

# 对于delta风险参数，使用Qiskit内置的delta计算函数量子线路
from qiskit_finance.applications.estimation import EuropeanCallDelta

# 参数num_state_qubits是存储样本用的量子比特数
# 参数strike_price是执行价格
# 参数bounds是ST的取样区间
# 参数uncertainty_model是ST的取样量子线路
european_call_delta = EuropeanCallDelta(
    num_state_qubits=num_uncertainty_qubits,
    strike_price=strike_price,
    bounds=(low, high),
    uncertainty_model=uncertainty_model,
)
# 绘制量子线路
european_call_delta._objective.decompose().draw()

         ┌──────┐
state_0: ┤0     ├
         │      │
state_1: ┤1     ├
         │      │
state_2: ┤2     ├
         │  cmp │
state_3: ┤3     ├
         │      │
 work_0: ┤4     ├
         │      │
 work_1: ┤5     ├
         └──────┘

# 设置振幅估计需要的精度参数
epsilon = 0.01
alpha = 0.05

# 创建一个量子虚拟机实例（在传统计算机里模拟）
qi = QuantumInstance(Aer.get_backend("aer_simulator"), shots=100)
# 从内置的欧式看涨期权的定价实现中取出需要振幅估计的问题
problem = european_call_delta.to_estimation_problem()

# 构建一个振幅估计IterativeAmplitudeEstimation
ae_delta = IterativeAmplitudeEstimation(epsilon, alpha=alpha, quantum_instance=qi)
# 启动振幅估计器，即重复执行量子线路并进行测量
result_delta = ae_delta.estimate(problem)
# 从结果中取出期权delta风险参数在95%（1-alpha）概率下的置信区间
conf_int = np.array(result_delta.confidence_interval_processed)

print("期权delta风险参数数值解：          \t%.4f" % exact_delta)
print("期权delta风险参数量子算法解:       \t%.4f" % european_call_delta.interpret(result_delta))
print("期权delta风险参数95%%概率置信区间：\t[%.4f, %.4f]" % tuple(conf_int))

期权delta风险参数数值解：          	0.4944
期权delta风险参数量子算法解:       	0.4965
期权delta风险参数95%概率置信区间：	[0.4884, 0.5047]

4. 其他参考资料

主要的参考资料都已经嵌入到上文中的超链接中了，未嵌入的参考资料如下：
《欧式看涨期权定价》：Qiskit的文档。本文中的代码就是对此文档里的代码的略加修正和解读。
《量子风险分析》：自然周刊2019年2月上的一篇论文，是上面Qiskit文档的理论依据之一。
《量子金融白皮书》：本源量子最近发布的量子计算在金融行业应用的白皮书。
《量子计算与编程入门》：本源量子发布的免费的量子计算入门开源读物，从原理到实践都有涉及。