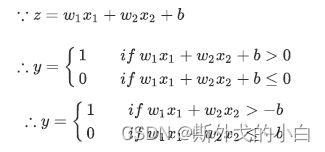pytorch_lesson8 单层线性回归+二分类逻辑回归+多分类softmax
注:仅仅是学习记录笔记,搬运了学习课程的ppt内容,本意不是抄袭!望大家不要误解!纯属学习记录笔记!!!!!!
文章目录
- 一、单层回归网络:线性回归
-
- 1、单层回归网络的理论基础
- 2 tensor实现单层神经网络的正向传播
- 3 tensor新手陷阱
-
- tensor计算中的第一大坑:PyTorch的静态性
- tensor计算中的第二大坑:精度问题
- 4 torch.nn.Linear实现单层回归神经网络的正向传播
- 二、二分类神经网络:逻辑回归
-
- 1 二分类神经网络的理论基础
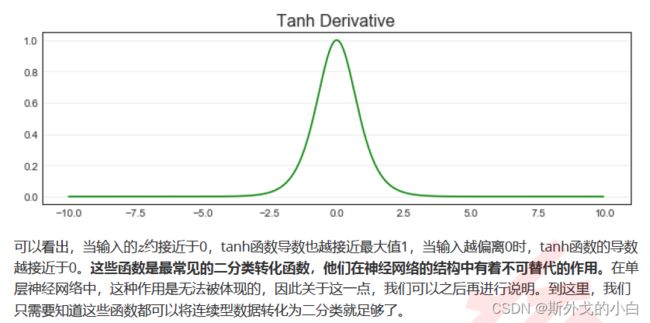
- 2 符号函数sign,ReLU,Tanh
-
- sign
- ReLU
- tanh
- 3 torch.functional实现单层二分类神经网络的正向传播
- 三、多分类神经网络:softmax
-
- 1 认识softmax函数
- 2 pytorch中的softmax函数
- 3 使用nn.Linear与functional实现多分类神经网络的正向传播
一、单层回归网络:线性回归
1、单层回归网络的理论基础
线性回归算法是机器学习中最简单的回归类算法,多元线性回归指的就是一个样本对应多个特征的线性回归问题。假设我们的数据现在就是二维表,对于一个有个特征的样本而言,它的预测结果可以写作一个几乎人人熟悉的方程:



如果在我们的方程里没有常量b,我们则可以不写X特征矩阵中的第一列以及中的权重矩阵第一行。
现在假设,我们的数据只有2个特征,则线性回归方程可以写作如下结构:
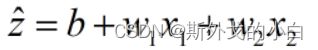
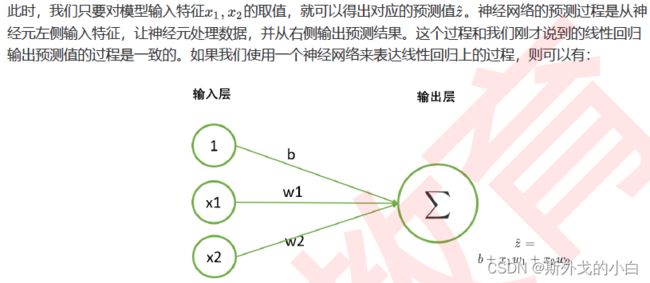
2 tensor实现单层神经网络的正向传播
让我们使用一组非常简单(简直是简单过头了)的代码来实现一下回归神经网络求解的过程,在神经
网络中,这个过程是从左向右进行的,被称为神经网络的正向传播(forward spread)(当然,这是正
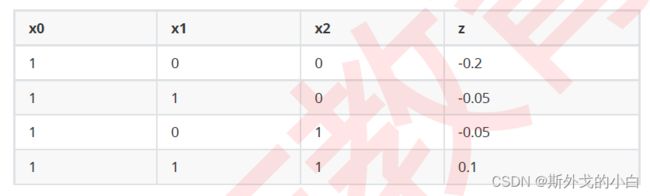
向传播中非常简单的一种情况)。来看下面这组数据:
#构造能够拟合以上数据的单层归回神经网络
import torch
X = torch.tensor([[1, 0, 0], [1, 1, 0], [1, 0, 1], [1, 1, 1]],dtype=torch.float32)
#x张量中第一列所有的数值为1,是为了跟偏置b相乘
y = torch.tensor([-0.2, -0.05, -0.05, 0.1])
w = torch.tensor([-0.2, 0.15, 0.15])
#w张量中, -0.2是bias偏置的数值
def linearR(X, w):
zhat = torch.mv(X, w)
return zhat
zhat = linearR(X, w)
print(zhat)
#tensor([-0.2000, -0.0500, -0.0500, 0.1000])
3 tensor新手陷阱
当我们输入的是整数时,默认生成的int64的类型,当我们输入的是浮点型数据时,默认生成的是float32的类型。
torch.mv矩阵和向量相乘时,向量必须是第二个参数。
tensor计算中的第一大坑:PyTorch的静态性
#我们使用大写的Tensor可以直接定义float类型,但这个方法并不推荐
x_ = torch.Tensor([[1, 0, 0], [1, 1, 0], [1, 0, 1], [1, 1, 1]])
print(x_.dtype)
#torch.float32
#或者就就养成好习惯,在构建张量的时候,直接定义张量的类型即可
X = torch.tensor([[1, 0, 0], [1, 1, 0], [1, 0, 1], [1, 1, 1]], dtype=torch.float32)
tensor计算中的第二大坑:精度问题
print(zhat == y)
#tensor([ True, False, False, False])
SSE = sum((y - zhat) ** 2)
print(SSE)
#tensor(8.3267e-17)
为什么会出现这种情况呢?因为求解的预测值和真实值看起来是一样的。
preds = torch.ones(300, 68, 64, 64)
print(preds.sum())
#tensor(83558400.)
preds = torch.ones(300, 68, 64, 64) * 0.1
print(preds.sum() * 10)
#tensor(83558336.)
主要的原因是张量在定义的时候,默认的精度是32位,所以在计算的过程中存在一些精度的问题。
与Python中存在Decimal库不同,PyTorch设置了64位浮点数来尽量减轻精度问题
preds = torch.ones((300, 68, 64, 64), dtype=torch.float64)
print(preds.sum() * 10)
#tensor(8.3558e+08, dtype=torch.float64)
4 torch.nn.Linear实现单层回归神经网络的正向传播
import torch
X = torch.tensor([[0, 0], [1, 0], [0, 1], [1, 1]], dtype=torch.float32)
Output = torch.nn.Linear(2, 1) #特征一共有两个,也就是列的个数,输出的时候只需要一个神经元
zhat = Output(X)
print(zhat)
'''
tensor([[ 0.1883],
[ 0.0015],
[-0.0536],
[-0.2404]], grad_fn=)
'''
(1)nn.Linear是一个类,在这里代表了输出层,所以我使用output作为变量名,output = 的这一行相当于是类的实例化过程;
(2)实例化的时候,nn.Linear需要输入两个参数,分别是(上一层的神经元个数,这一层的神经元个数)。上一层是输入层,因此神经元个数由特征的个数决定(2个)。这一层是输出层,作为回归神经网络,输出层只有一个神经元。因此nn.Linear中输入的是(2,1);
(3)我只定义了X,没有定义w和b。所有nn.Module的子类,形如nn.XXX的层,都会在实例化的同时随
机生成w和b的初始值。所以实例化之后,我们就可以调用以下属性来查看生成的w和b:
print(Output.weight) #查看生成的w
'''
Parameter containing:
tensor([[0.6750, 0.5684]], requires_grad=True)
'''
print(Output.bias)
'''
Parameter containing:
tensor([0.1965], requires_grad=True)
'''
其中,w是必然会生成的,b是我们可以控制是否要生成的。在nn.Linear类中,有参数bias,默认
bias = True。如果我们希望不拟合常量b,在实例化时将参数bias设置为False即可:
Output = torch.nn.Linear(2, 1, bias=False)
print(Output.weight)
'''
Parameter containing:
tensor([[ 0.4493, -0.5164]], requires_grad=True)
'''
print(Output.bias)
#None
由于w和b是随机生成的,所以每次代码运行之后的结果都不一致,我们希望控制随机性,就可以使用torch的random类。如下所示:
torch.random.manual_seed(420)
output = torch.nn.Linear(2, 1)
zhat = output(X)
print(zhat)
(1)由于不需要定义常量b,因此在特征张量中,也不需要留出与常数项相乘的x0那一列,在输入数据时,我们只输入了两个特征x1, x2;
(2)输入层只有一层,并且输入层的结构(神经元的个数)由输入的特征张量X决定,因此在pytorch中建立神经网络时,不需要定义是输入层;
(3)实例化之后,将特征张量输入到实例化的类中,即可得到输出层的输出结果。
二、二分类神经网络:逻辑回归
1 二分类神经网络的理论基础
在实际生活中,变量之间的关系通常不是一条直线,而是呈现某种曲线关系。统计学家们再线性回归的方程两边引入了联系函数,对线性回归的方程做出了各种各样的变坏,并将这些变化的方程称为“广义线性回归”。

sigmoid函数能够带来奇妙的变化




更神奇的是,当我们对线性回归的结果取sigmoid函数之后,只要再进行以下操作:
1)将结果以几率的形式展现
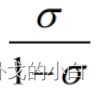
2)在几率上求e为底的对数
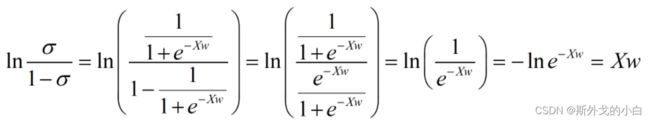


2 tensor实现二分类神经网络的正向传播

import torch
X = torch.tensor([[1, 0, 0], [1, 1, 0], [1, 0, 1], [1, 1, 1]], dtype=torch.float32)
andgate = torch.tensor([[0], [0], [0], [1]], dtype=torch.float32)
#保险起见,生成二维的.float32类型的标签
w = torch.tensor([-0.2, 0.15, 0.15], dtype=torch.float32)
def LogisticR(X, w):
zhat = torch.mv(X, w)
sigma = torch.sigmoid(zhat)
#sigma = torch.sigmoid(1/ 1 + torch.exp(-zhat))
andgate = torch.tensor([int(x) for x in sigma >= 0.5], dtype=torch.float32)
return zhat, sigma, andgate
zhat,sigma, andhat = LogisticR(X, w)
print(zhat, sigma, andgate)
'''
tensor([-0.2000, -0.0500, -0.0500, 0.1000])
tensor([0.4502, 0.4875, 0.4875, 0.5250])
tensor([[0.],
[0.],
[0.],
[1.]])
'''
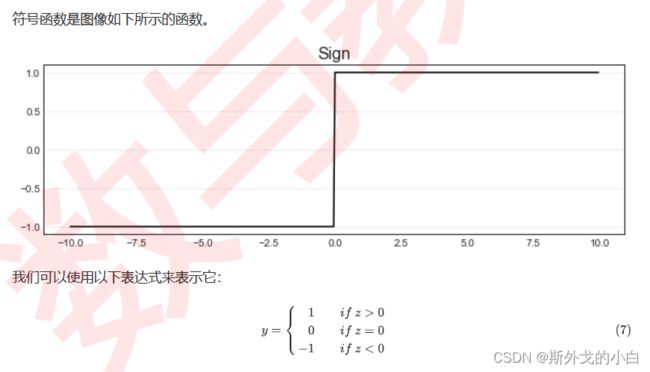
2 符号函数sign,ReLU,Tanh
sign
X = torch.tensor([[1, 0, 0], [1, 1, 0], [1, 0, 1], [1, 1, 1]], dtype=torch.float32)
andgate = torch.tensor([[0], [0], [0], [1]], dtype=torch.float32)
#保险起见,生成二维的.float32类型的标签
w = torch.tensor([-0.2, 0.15, 0.15], dtype=torch.float32)
def LogisticRwithsign(X, w):
zhat = torch.mv(X, w)
andgate = torch.tensor([torch.ceil(x) for x in zhat], dtype=torch.float32)
return zhat, andgate
LogisticRwithsign(X, w)
print(zhat, andgate)
'''
tensor([-0.2000, -0.0500, -0.0500, 0.1000])
tensor([[0.],
[0.],
[0.],
[1.]])
'''
ReLU
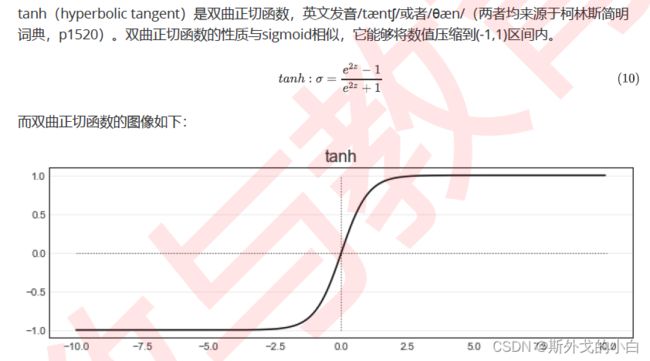
tanh
def LogisticRwithtanh(X, w):
zhat = torch.mv(X, w)
tanh = torch.tanh(zhat)
andgate = torch.tensor([int(x) for x in tanh >= 0], dtype=torch.float32).reshape(4, 1)
return zhat, tanh, andgate
zhat, tanh, andgate = LogisticRwithtanh(X, w)
print(zhat, tanh, andgate)
'''
tensor([-0.2000, -0.0500, -0.0500, 0.1000])
tensor([-0.1974, -0.0500, -0.0500, 0.0997])
tensor([[0.],
[0.],
[0.],
[1.]])
'''
3 torch.functional实现单层二分类神经网络的正向传播
import torch
from torch.nn import functional as F
X = torch.tensor([[0, 0], [1, 0], [0, 1], [1, 1]], dtype=torch.float32)
torch.random.manual_seed(420) #人为设置随机种子
dense = torch.nn.Linear(2, 1)
zhat = dense(X)
sigma = F.sigmoid(zhat)
#符号函数sign
#sign = torch.sign(zhat)
#Relu函数
#relu = torch.relu(zhat)
#tanh函数
#tanh =torch.tanh(zhat)
yhat = [int(x) for x in sigma > 0.5]
三、多分类神经网络:softmax
1 认识softmax函数
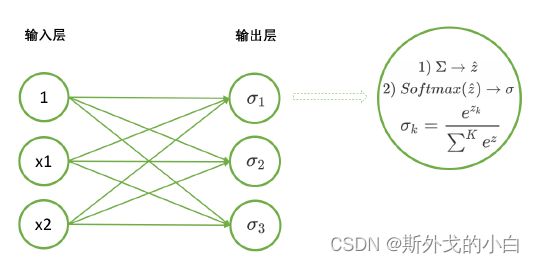
Softmax函数是深度学习基础中的基础,它是神经网络进行多分类时,默认放在输出层中处理数据的函数。假设现在神经网络是用于三分类数据,且三个分类分别是苹果,柠檬和百香果,序号则分别是分类2和分类3。则使用softmax函数的神经网络的模型会如下所示:

2 pytorch中的softmax函数
s = torch.tensor([[[1, 2], [3, 4], [5, 6]], [[5, 6], [7, 8], [9, 10]]], dtype=torch.float32)
print(s.ndim)
#2
print(s.shape)
#torch.Size([2, 3, 2])
print(torch.softmax(s, dim=0))
'''
tensor([[[0.0180, 0.0180],
[0.0180, 0.0180],
[0.0180, 0.0180]],
[[0.9820, 0.9820],
[0.9820, 0.9820],
[0.9820, 0.9820]]])
'''
#在整个张量中,有两个张量,一个二维张量就是一类
print(torch.softmax(s, dim=0))
'''
tensor([[[0.0180, 0.0180, 0.5000, 0.5000],
[0.0180, 0.0180, 0.5000, 0.5000],
[0.0180, 0.0180, 0.5000, 0.5000]],
[[0.9820, 0.9820, 0.5000, 0.5000],
[0.9820, 0.9820, 0.5000, 0.5000],
[0.9820, 0.9820, 0.5000, 0.5000]]])
'''
#在整个张量中,有两个张量,一个二维张量就是一类
print(torch.softmax(s, dim=1))
'''
tensor([[[0.0159, 0.0159, 0.3333, 0.3333],
[0.1173, 0.1173, 0.3333, 0.3333],
[0.8668, 0.8668, 0.3333, 0.3333]],
[[0.0159, 0.0159, 0.3333, 0.3333],
[0.1173, 0.1173, 0.3333, 0.3333],
[0.8668, 0.8668, 0.3333, 0.3333]]])
'''
#在一个二维张量中,有三行数据,每一行就是一类
print(torch.softmax(s, dim=2))
#在每一行中,有4个数据,每个数据就是一个类别
'''
tensor([[[0.0128, 0.0347, 0.2562, 0.6964],
[0.0723, 0.1966, 0.1966, 0.5344],
[0.1966, 0.5344, 0.0723, 0.1966]],
[[0.1966, 0.5344, 0.0723, 0.1966],
[0.2562, 0.6964, 0.0128, 0.0347],
[0.2671, 0.7262, 0.0018, 0.0049]]])
'''
在实际中,训练神经网络时往往会使用softmax函数,在预测时就不再适用softmax函数,而是直接读取结果最大的z对应的类比即可。
3 使用nn.Linear与functional实现多分类神经网络的正向传播
X = torch.tensor([[0, 0], [1, 0], [0, 1], [1, 1]], dtype=torch.float32)
torch.random.manual_seed(420)
dense = torch.nn.Linear(2, 3)
zhat = dense(X)
sigma = F.softmax(zhat, dim=1) #此时需要进行维度1来进行区分
print(zhat)
'''
tensor([[ 0.5453, 0.2653, -0.3527],
[ 0.9772, 0.9382, -0.5684],
[ 0.1197, -0.2964, -0.8400],
[ 0.5516, 0.3765, -1.0557]], grad_fn=)
'''
print(sigma.shape)
#torch.Size([4, 3])
print(sigma)
'''
tensor([[0.4623, 0.3494, 0.1883],
[0.4598, 0.4422, 0.0980],
[0.4896, 0.3229, 0.1875],
[0.4902, 0.4115, 0.0983]], grad_fn=)
'''
这里之所以用dim=1,是因为这四个变量都需要计算出对应着的三个分类的概率值,所以每一个值都是一个类,按照列计算softmax