【强化学习】概念梳理：强化学习、马尔科夫决策过程与动态规划

上一篇推文中，我们介绍了Q-learning，这是一种off-policy的算法，也是一种近似动态规划算法，其主要思想是评估每个状态$s\in S$下做出动作$a$的期望总回报，并基于评估出的state-action value信息，也就是Q-table来做决策。

但是在学习强化学习的时候，我们总是看到马尔科夫决策过程(Markov decision process)这个词，下面我们来梳理一下他们之间的关系。

首先我们来复习一下相关概念。

参考文献
Lawler, Gregory F. Introduction to stochastic processes. Chapman and Hall/CRC, 2018.
参考网址
https://towardsdatascience.com/introduction-to-reinforcement-learning-markov-decision-process-44c533ebf8da

动态规划(Dynamic programming)

动态规划(Dynamic programming, DP)是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划由美国数学家R.Bellman 等人在研究多阶段决策过程的优化问题时提出。

1. Richard Bellman. On the theory of dynamic programming. Proceedings of the National
   Academy of Sciences of the United States of America, 38(8):716, 1952.
2. Richard Bellman. Dynamic programming. Science, 153(3731):34–37, 1966.

动态规划的基本思想是：要解一个给定问题，如果问题满足一定的性质，我们可以将分拆为很多部分（即子问题），并逐一求解，再根据子问题的解得出原问题的解。

运用动态规划求解的问题一般具备如下特点：

• (1) 无后效性(无记忆性/马尔科夫性)：某个阶段的状态一旦确定后，就不会受该状态之后的决策影响，同时，该阶段之后的决策和状态发展不受该阶段之前的各状态的影响。
• (2) 最优子结构：如果某个问题的最优解可以由其子问题的最优解推出，那么该问题就具备最优子结构。简言之，一个最优策略的子策略总是最优的，就叫做最优子结构，也叫作最优化原理。例如在一个有向无环图，且无负环的图中，找寻最短路。其最短路中任何两个节点之间的路径，也是以那两个节点为起始点和终点的最短路。例如,$G=(V,A)$，给定起点为0， 终点为15，假设其最短路为$[0,1,3,7,4,6,10,8,15]$，则我们从最短路中找到两个点，例如为3和6，则从3出发，到达点6的最短路为$[3,7,4,6]$。
• (3) 子问题的重叠性：动态规划在实现过程中需要存储各种状态，这些状态会占用计算空间，如果要使得动态规划算法能够比较高效，那么各种状态就要有较高的复用性，以便减少计算空间的占用。但该性质不是必须的，只是在一定程度上决定了算法的效率。

用动态规划求解多阶段决策问题，我们首先需要定义好阶段、状态、允许决策集合、状态转移方程、策略、指标函数和最优值函数。

• 阶段:用正整数$k=1,2,3\cdots$表示;
• 状态：第$k$阶段的状态用$S_k$表示，这里需要定义可达状态集合，比如$S_2\in \{休息，学习，上课\}$
• 决策和允许决策集合: 用$a_k(s_k)$表示在状态$s_k$下做的决策，用$D_k(s_k)$表示在状态$s_k$下的允许决策集合。我们有$a_k(s_k)\in D_k(s_k)$. (这就相当于强化学习中的action 集合$A$)
• 策略：策略是一个按顺序排列的决策组成的集合。 由过程的第 $k$ 阶段开始到终止状态为止的过程(记为第$n$阶段) , 称为问题的后部子过程( 或称为$k$ 子过 程) 。 由每段的决策按顺序排列组成的决策函数序列$\{a_k(s_k),a_{k+1}(s_{k+1}),\cdots ,a_n(s_n)\}$称为$ k $子过程策略 , 简称子策略 , 记为 $p_{k,n}(s_k)$，也就是从第$k$阶段到终止阶段的决策序列。即$$p_{k,n}(s_k)=\{a_k(s_k),a_{k+1}(s_{k+1}),\cdots ,a_n(s_n)\}$$。当 $k=1$ 时 , 此决策函数序列称为全过程的一个策略 , 简称策略, 记为 $p_{1,n}(s_1)$。在实际问题中 , 可供选择的策略有一定的范围, 此范围为允许策略集合。 从允许策略集合中找出达到最优效果的策略称为最优策略。
• 状态转移方程也就对应强化学习(马尔科夫决策过程)中的状态转移概率矩阵$P_{s,s^{\prime }}^a$。状态转移方程是确定过程由一个状态到另一个状态的演变过程。 若给定第 $k$ 阶段状态变量$s_k$ 的值 , 如果该段的决策变量 $a_k$一经确定 , 第 $k+1$ 阶段的状态变量 $s_{k+1}$ 的值也就完全确定。 即$s_{k+1}$ 的值随 $s_k$ 和 $a_k$ 的值变化而变化。 这种确定的对应关系 , 记为$$s_{k+1}=T_k(s_k,a_k)$$。上式描述了由$k$ 阶段到 $k+1$ 阶段的状态转移规律 , 也被称为状态转移方程。 $T_k$ 称为状态转移函数。 例如在最短路中，$s_{k+1}=T_k(s_k=1,a_k=2)=2$,也就是，在点1，我们下一步访问2，那么下一阶段我们就到达了点2。
• 指标函数和最优值函数对应强化学习中的Action-Value function以及Optimal Action-Value function：用来衡量所实现过程优劣的一种数量指标 , 称为指标函 数。 它是定义在全过程和 所有后部子过程上确定的数量函数。 常用 $V_{k,n}$ 表示,也就是从第$k$阶段到第$n$阶段的累计价值。 即$$V_{k,n}=V_{k,n}(s_k,a_k,s_{k+1},a_{k+1},\cdots ,s_{n+1}),\forall k=1,2,\cdots ,n$$。对于要构成动态规划模型的指标函数 , 应具有可分离性 , 并满足递推关系。 即$V_{k,n}$ 可以表示为 $s_k、u_k、V_{k+1},n$ 的函数。 记为$$V_{k,n}(s_k,a_k,s_{k+1},a_{k+1},\cdots ,s_{n+1})=\varphi [s_k,a_k,V_{k,n}(s_{k+1},a_{k+1},\cdots ,s_{n+1})]$$。这也反映了无记忆性。之后发生的事，只和当前状态和动作，以及之后的事情有关，与之前发生的事情无关。指标函数的最优值 , 称为最优值函数 , 记为$f_k(s_k)$。 它表示从第$k $阶段的状态$s_k$ 开始到第$n$阶段的终止状态的过程 , 采取最优策略所得到的指标函数值。 即$$f_k(s_k)=\underset{a_k,\cdots ,a_n}{\mathrm{opt}}{V}_{k,n}(s_k,a_k,s_{k+1},a_{k+1},\cdots ,s_{n+1})$$。其中，opt可以是$\max$或者$\min$。
  -动态规划基本方程或者贝尔曼方程:定义好上述元素，接下来如何求解呢？这时候就要用到大名鼎鼎的贝尔曼方程了，即$$f_k(s_k)=\underset{a_k\in D_k(s_k)}{\mathrm{opt}}\{v_k(s_k,a_k(s_k))+f_{k+1}(a_k(s_k))\}$$。其中，opt可以是$\max$或者$\min$。该方程需要一个边界条件，即$$f_{n+1}(s_{n+1})=0$$。当然这里有顺序解法和逆序解法下的方程，这里不做涉及。

Note：贝尔曼方程$$f_k(s_k)=\underset{a_k\in D_k(s_k)}{\mathrm{opt}}\{v_k(s_k,a_k(s_k))+f_{k+1}(a_k(s_k))\}$$也是反应了无后效性的特点。

Note 2: 我们来对比动态规划中的贝尔曼方程$$f_k(s_k)=\underset{a_k\in D_k(s_k)}{\mathrm{opt}}\{v_k(s_k,a_k(s_k))+f_{k+1}(a_k(s_k))\}$$，与强化学习中我们使用的贝尔曼方程$$Q^{\ast }(s_t,a_t)=\mathbb{E}[R_t+\gamma Q^{\ast }(S_{t+1},A_{t+1})|S_t=s_t]$$,或者
$$V(s_t)=\mathbb{E}[R_t+\gamma V(S_{t+1})|S_t=s_t]$$
形式是相同的。特别地，从含义上来讲，动态规划中的$f_k(a_k(s_k))$就相当于强化学习中的$Q^{\ast }(s_t,a_t)$，区别在于，动态规划中，贝尔曼方程是可以精确求解的。但是在强化学习中，$R_t$是随机的或者未知的；且$Q^{\ast }(s_t,a_t)$也通常是未知形式，需要用迭代算法去近似。

以上参考自：《运筹学》教材编写组. 运筹学. 2012.

其中，各个部分与强化学习(马尔科夫决策过程)的对应关系如下：

• 阶段其实就是强化学习中常见的时间戳$t$
• 状态跟强化学习(马尔科夫决策过程)中相同，也就是$S$
• 决策和允许决策集合也就是强化学习(马尔科夫决策过程)中的action，也就是$A$
• 策略：对应强化学习中的策略(policy)，但是区别在于，强化学习中的策略$\pi$是一个概率分布，而动态规划中的policy是一个确定的决策集合。
• 状态转移方程也就对应强化学习(马尔科夫决策过程)中的状态转移概率矩阵$P_{s,s^{\prime }}^a$
• 指标函数和最优值函数对应强化学习中的Action-Value function以及Optimal Action-Value function

但是动态规划与强化学习的区别在于：

• 状态转移函数：强化学习中，状态转移是一个已知或者是未知的状态转移概率矩阵$P_{s,s^{\prime }}^a$，而在传统动态规划中，状态转移是一个确定的函数，即$$s_{k+1}=T_k(s_k,a_k)$$,也就是说，在动态规划中，在状态$s_k$，采取决策(动作)$a_k$，下一阶段的状态是完全确定的，可以根据状态转移函数计算得出。而强化学习中，根据状态转移概率矩阵$P_{s,s^{\prime }}^a$随机生成下一阶段的状态(model based reinforcement learning)，或者是由环境反馈得到下一阶段的状态(model free)。这里我其实有一个疑问，如果状态转移概率矩阵$P_{s,s^{\prime }}^a$已知，确实也可以用动态规划求解，但是跟我了解的传统动态规划不同。这里希望和读者们进一步探讨确认。
• 决策：在传统的动态规划中，决策必须是确定的，不能是概率分布。而强化学习的policy based方法中，是允许给一个policy的，即每个动作取值的概率。例如：向左：概率为0.8；向右：概率为0.2。这里也有一个疑问，就是我所理解的动态规划中，这个策略是确定的，不会是一个概率分布。当然，如果用动态规划求解MDP，我觉得是没问题的。只是这里还是有一点疑惑。
• reward:在动态规划中，进行一步动作$a_k$，由于下一阶段的状态是可以按照状态转移方程$s_{k+1}=T_k(s_k,a_k)$精确的计算出来，也就是可以精确的预测出来，因此immediate reward是可以精确的计算出来的。但是在强化学习中，immediate reward一般是环境给出的，具有一定的随机性。当然，一些问题中，immediate reward也是可以定义的，因此也是可以定义出来。但是区别就在于，用户自己定义的immediate reward，只是基于自己的目的设计的，它与真正的能够使得最后的目标函数最大化的方向不一定是一样的。用户也只能通过摸索去尝试，如果运气好，reward设计的好，就可以使得算法很好的收敛，如果设计的不好，则会遇到收敛困难等问题。但是动态规划中，immediate reward是可以很准确的与整体的目标贴合的，具体来讲，immediate reward其实就是目标函数的计算方法，在一开始就精确的定义好了。

马尔科夫链（Markov Chain）

马尔科夫链是随机过程中一个重要的概念。要了解马尔科夫链，我们首先需要回顾一下随机过程。

随机过程(stochastic process)
一个随机过程$\{X_t,t\in T\}$就是一系列随机变量的序列。
– A stochastic process $\{X_t,t\in T\}$ is a family of random variables.
– 例如抛100次硬币，其正面朝上(1)还是反面朝上(0)的状态序列，就是一个随机过程: $[0,0,1,1,0,1,0,\cdots ]$
– 随机过程并没有强调随机变量之间的关系，比如，并不要求具有无后效性等，只要是一些列随机变量的序列，都叫做随机过程。

基于随机过程的概念，马尔科夫链的定义如下：

马尔科夫链（Markov Chain）
若一个随机过程$\{X_n,n=0,1,2,\cdots \}$,其状态空间(state space)是有限的，且对于其所有状态$i_0,i_1,\cdots ,i_{n-1},i,j$以及所有的$n⩾0$，均满足

$$\begin{array}{rl}& P\left\{X_{n+1}=j|X_0=i_0,X_1=i_1,X_2=i_2,\cdots ,X_{n-1}=i_{n-1},X_n=i\right\}\\ =& P\left\{X_{n+1}=j|X_n=i\right\}\end{array}$$
则该随机过程被称之为一个马尔科夫链。我们也将上述性质叫做马尔可夫性或者无记忆性或者无后效性.
如果$P\left\{X_{n+1}=j|X_n=i\right\}$随着$n$的变化不改变，则我们说该马尔科夫链拥有稳态转移概率。

为了方便，我们做一个简写，即
$$P_{ij}=P\left\{X_{n+1}=j|X_n=i\right\}$$

从上述概念可以得出。马尔科夫链：

1. 是一个随机过程；
2. 满足马尔可夫性或者无记忆性或者无后效性.
3. 状态空间有限。

在后续探讨中，我们会用到一个重要概念：单步状态转移概率(one-step transition probabilities) $P_{ij}$
$$P=\left[\begin{array}{cccc}{P}_{00}& P_{01}& P_{02}& \cdots \\ P_{10}& P_{11}& P_{12}& \cdots \\ ⋮& ⋮& ⋮& ⋮\\ P_{n0}& P_{n1}& P_{n2}& \cdots \\ ⋮& ⋮& ⋮& ⋮\end{array}\right]$$
其中，$P_{ij}$表示当前状态为$j$，下一步状态为$j$的概率。单步状态转移概率矩阵$P$满足：

1. $P_{ij}⩾0,\forall i,j=0,1,2,\cdots$，即概率非负。
2. ${\sum }_{j=0}^{\infty }{P}_{ij}=1,\forall i=0.1.,\cdots$，每一行概率相加为1，也就是在一个状态$i$下，下一个状态必然在状态空间中。

• 我们举一个马尔科夫链的简单例子：未来15天的天气情况。我们只考虑3种天气：晴天(1)，阴天(2)，多云(3)。则未来15天的天气情况就是一个马尔科夫链：$[1,1,3,2,\cdots ]$。

• 单步状态转移概率矩阵$P$为
  $$P=\left[\begin{array}{ccc}0.3& 0.2& 0.5\\ 0.2& 0.4& 0.4\\ 0.5& 0.3& 0.2\end{array}\right]$$

• 马尔科夫链中，并没有引入动作(action)的概念，仅仅是考虑不同时刻之间的状态变化是满足马尔可夫性的，且状态之间的转换是具有随机性的。也就是说，马尔科夫链中，并没有明确地引入决策的概念，没有强调一个决策者(也就是agent)应该如何在这种随机的环境中做决策。

• 而马尔科夫决策过程(Markov decision process)则是将决策引入随机过程，试图让决策主体(agent)做出最优的决策。

马尔科夫决策过程和强化学习

上面提到，马尔科夫决策过程(Markov decision process)将决策主体agent的决策或者动作(action)引入了系统，试图解决一个决策者(也就是agent)应该如何在这种随机的环境中做决策的问题。

马尔科夫决策过程(Markov decision process)
考虑一个具有有限状态的过程(状态索引为0,1,2,…)，其在时刻$t=0,1,2,\cdots$下被观测到处于一个可能的状态之中。在过程的状态被观测到之后，一个动作必须被选择并且执行。用$A$表示所有可能动作的集合，且$A$中的元素是有限的。
如果该过程在时刻$t$处在状态$i$，且动作$a$被选择执行，我们假设会发生下面两件事:

1. 产生成本$C(i,a)$;
2. 系统的下一个状态是根据状态转移概率$P_{ij}(a)$选取得到。
   我们用$X_t$表示过程在时刻$t$的状态，用$a_t$表示在时刻$t$执行的动作，则假设2可以等价为
   $$P\left\{X_{t+1}=j|X_0,a_0,X_1,a_1,\cdots ,X_t=i,a_t=a\right\}=P_{ij}(a)$$
   因此，成本$C(i,a)$和转移概率$P_{ij}(a)$都只是上一个状态$X_t=i$和接下来的动作$a$的函数。另外，我们假设成本$C(i,a)$是有界的，即$|C(i,a)|<M$，其中$M$是一个正数。

马尔科夫决策过程和强化学习息息相关。

参考：https://towardsdatascience.com/introduction-to-reinforcement-learning-markov-decision-process-44c533ebf8da

• 一般来讲，强化学习是一种专门用于解决序列决策问题的学习范式。根据强化学习，一个智能体(agent)根据它从环境中得到的反馈(包括状态转移以及奖励)学习如何做动作，使得agent获得的总期望收益最大化。在一个状态下采取动作的价值是由状态-动作函数来评估的，也称为Q函数(Q function)。
• 强化学习经常被用数学语言建模成为一个马尔科夫决策过程，并进一步进行求解的。这也就是马尔科夫决策过程和强化学习之间的关系。简略来讲，强化学习是一类解决问题的范式，在数学上，强化学习经常被建模为马尔科夫决策过程，而进一步被求解。这个关系，就跟混合整数规划和VRP的关系一样。

这里，我们也梳理一下马尔科夫链和马尔科夫决策过程的内容：
这里就参自https://stepneverstop.github.io/%E5%BC%BA%E5%8C%96%E5%AD%A6%E4%B9%A0%E4%B9%8BMDP%E9%A9%AC%E5%B0%94%E7%A7%91%E5%A4%AB%E5%86%B3%E7%AD%96%E8%BF%87%E7%A8%8B.html

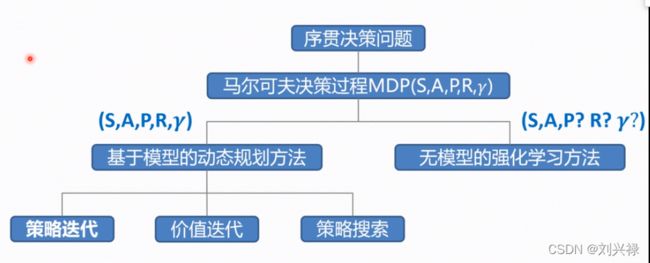
根据上述描述，强化学习和马尔科夫决策过程的关系是：强化学习问题在数学上，通常被建模成为一个马尔科夫决策过程。

马尔科夫决策过程和动态规划

接下来我们来阐明，动态规划和马尔科夫决策过程的关系。我们直接给出结论：

• 动态规划可以用于求解马尔科夫决策过程。并且从迭代的方式上一般有两类：值迭代(value iteration)和策略迭代(Policy Iteration)。也就是值迭代和策略迭代是两类动态规划算法，都属于动态规划算法，只不过由于具体细节不同，被称为不同的名字。
• 策略迭代(Policy Iteration)：找到最优策略$\pi (a|s)$。在策略迭代中，我们首先给定一个policy $\pi$，然后用初始化的value function $V_{\pi }(s)$ (比如，可以初始化$V_{\pi }(s)=0$)去评估该策略并更新value function $V_{\pi }(s)$，评估的方法，可以用贝尔曼方程。之后根据该策略做贪婪决策(act greedy),然后生成新的策略${\pi }^{\prime }$，重复以上过程，直到收敛。算法迭代中包括：策略评估(policy evaluation)和策略提升/改进(policy improvements)。Policy Iteration最后可以同时得到价值函数$V_{\pi }(s)$和策略$\pi$。这里不做展开。
  – 这里跟动态规划求解最短路等问题是一样的。例如Dijkstra算法中，会用标签记录到达每个节点的最短距离$d_v$，以及存储到达这个节点$v$的前序节点$u$。根据每个节点的前序节点$u$，就可以从起点开始，得到最短路。这个前序节点，就相当于这里的策略$\pi$，到达每个节点的最小距离$d_v$，就相当于这里的价值函数$V_{\pi }(s)$。
• 值迭代(value iteration)：Value iteration 是Policy Iteration的一个特例.当Policy Iteration中的policy evaluation在第一步以后就停止，这就变成了Value iteration。在Value iteration中，我们可以从一些随机的Value function（比如:零）开始，然后我们用贝尔曼最优方程来迭代这个过程。也就是说，我们通过在贝尔曼最优方程中插入前一次迭代的值来计算一个状态的新价值函数。我们迭代这个过程，直到它收敛到最优价值函数，然后从这个最优价值函数计算出最优策略。

动态规划和一些其他相关内容之间的关系如图所示。

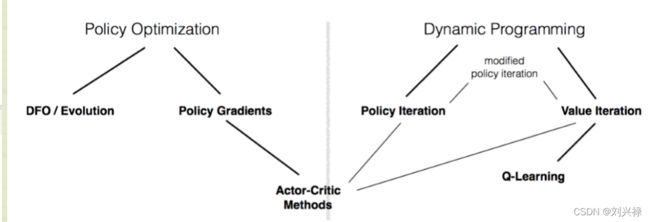
(本图来自：https://blog.csdn.net/qq_30615903/article/details/80762758)

当然还有一个总结的不错的图

(图来自https://www.bilibili.com/video/BV14f4y137Yh?p=1&share_medium=iphone&share_plat=ios&share_session_id=FAC19F1D-AA42-447C-9432-AAAF3F4825D9&share_source=WEIXIN&share_tag=s_i×tamp=1644993959&unique_k=cFjA4vw)

大致搞明白二者之间的关系之后，我们来梳理一下强化学习中的若干概念。

强化学习的基本概念

本节的概念，部分以游戏《超级马里奥》为背景进行介绍。
参考自Shusen Wang的视频：
https://www.bilibili.com/video/BV1rv41167yx?from=search&seid=18272266068137655483&spm_id_from=333.337.0.0

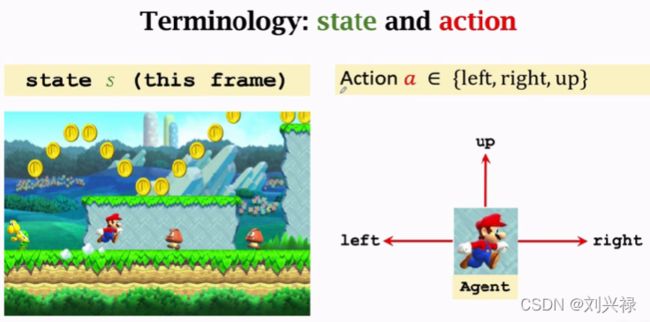
状态(State)和动作(Action)

State $s$: 当前所处的状态，上图中就是这一帧的画面(frame)，包括马里奥的位置，金币的位置，敌人的位置等
Action $a$：agent(智能体)可以选择的动作。action $\in \{\text{left, right, up}\}$,其实这里还应该有个stay，stay也是一个动作
Agent：发出动作的主体，动作是由谁做的谁就是agent

策略(Policy) $\pi$

policy的意思就是根据观测到的状态。做出一系列决策来控制agent运动，比如一局游戏中控制马里奥做动作的决策。
在数学上，Policy $\pi$是一个概率密度函数 ，用$\pi$表示，它满足

1. $\pi :(s,a)\to [0,1]$
2. $\pi (a|s)=\mathbb{P}(A=a|S=s)$

注意：大写表示是随机变量(random variable)，小写表示观测值(observation)

• 这里注意，给定状态$S=s$,下一步的具体动作$a$是根据policy $\pi (a|s)$随机抽样得到的，因此具有随机性。
• 给定了策略函数$\pi (a|s)$，我们就可以根据$\pi (a|s)$做决策。比如，控制马里奥玩游戏闯关等。

State transition

• 状态转移：当前状态$s$下，agent采取一个动作$a$，环境就会给一个新的状态$s^{\prime }$。
• 状态转移可以是确定的，也可以是随机的
  状态转移的随机性是从环境(environment)中来的。

状态转移函数
$$\begin{array}{r}p(s^{\prime }|s,a)=\mathbb{P}(S^{\prime }=s^{\prime }|S=s,A=a)\end{array}$$

• 确定的状态转移，或者状态转移概率已知，其实就是model based reinforcement learning.
• 未知的状态转移概率，一般就是model free reinforcement learning.

reward和return

下面是两个重要的概念: reward和return，其中：

• reward$R_t$：在时刻$t$，agent在采取了某个动作之后，环境返回的即时奖励（immediate reward）。这个即时奖励带有随机性，也就是随机的。由于他是个随机变量，因此我们用$R$来表示。
• return$U_t$ (Cumulative future reward): 从当前时刻开始，到过程结束，agent获得的累计奖励。

也就是$$U_t=R_t+R_{t+1}+R_{t+2}+\cdots$$

在强化学习中，我们是追求$U_t$的最大化。其实就是最大化$U_t$的期望。

• 其实这里，我们有$Q(s_t,a_t)=\mathbb{E}[U_t|S_t=s_t,A_t=a_t]$，我们用算法评估出$U_t$的期望$Q(s_t,a_t)$，然后基于$Q(s_t,a_t)$做决策。 (因为$U_t$也是随机变量)

• 这里，即时奖励写成小写$r$，表示已经是实现值了。但是实际上，即时奖励是一个随机变量$R$。
• 我们在下文中，统一用$R$表示随机变量，用$r$表示实现值。

在上式中，我们是把所有时刻的收益都同等对待了，比如今天立刻得到1000元和1年后得到1000元被同等对待了。这显然是不合理的。为了体现收益的时间价值，折扣因子(discount factor)$\gamma$被引入了。

Discount Factor ($\gamma$):

• 它决定了即时奖励（immediate reward）和未来奖励（future rewards）的重要性。即今天立刻得到1000元和1年后得到1000元不是同等重要的。这里实际上是做了简化处理，引入一个倍数关系。

基于此，则累计奖励$U_t$可以被重写为
$$\begin{array}{rl}{U}_t& =R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+\cdots \\ =& \sum _t^{\infty }{\gamma }^k{R}_{t+k}\end{array}$$

并且，我们有
$$\begin{array}{rl}{U}_t& =R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+\cdots \\ & =R_t+\gamma (R_{t+1}+\gamma R_{t+2}+\cdots )\\ & =R_t+\gamma U_{t+1}\end{array}$$
这也是在后续的算法中更新Q value的重要依据。

这里我们插播一个小知识点:

一个马尔科夫链，可以被定义为如下的5元组：$(S,A,P,R,\gamma )$

• $S$: 状态的集合;
• $A$: 智能体可选的动作的集合;
• $P$: 状态转移概率矩阵;
• $R$: 智能体的动作所积累的奖励;
• $\gamma$: 折扣因子.

• 基于模型的动态规划方法中，$(S,A,P,R,\gamma )$，五元组所有信息均已知。

• 但是在model free的强化学习中，是$(S,A,P?,R?,\gamma ?)$, $?$表示未知。
  

这里需要强调$U_t$是随机的，由于$U_t=R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+\cdots$,因此其随机性来源于：

1. 动作是随机的：$\mathbb{P}[A=a|S=s]=\pi (a|s)$
2. 新的状态是随机的：$\mathbb{P}[S^{\prime }=s^{\prime }|S=s,A=a]=p(s^{\prime }|s,a)$
   因此，对于$i⩾t$，即时奖励$R_i$是跟状态$S_i$和动作$A_i$都有关(注意，这里$S_i$，$A_i$是随机变量)。

• 所以，给定$s_t$，期望总回报$U_t$是跟下面的随机变量都有关的：
  • $A_t,A_{t+1},A_{t+2},\cdots$
  • $S_{t+1},S_{t+2},\cdots$

因此，期望总回报$U_t$也是随机的。

Action-Value function

相当于动态规划中的指标函数$$V_{k,n}=V_{k,n}(s_k,a_k,s_{k+1},a_{k+1},\cdots ,s_{n+1}),\forall k=1,2,\cdots ,n$$

Action-Value function: $Q_{\pi }(s_t,a_t)$ (Policy based approach下的定义)
$$Q_{\pi }(s_t,a_t)=\mathbb{E}[U_t|S_t=s_t,A_t=a_t]$$

• $Q_{\pi }(s_t,a_t)$指在状态$S_t=s_t$时，采取动作$A_t=a_t$的期望总回报。
• $Q_{\pi }(s_t,a_t)$是跟策略函数$\pi$以及状态$s$和动作$s$有关的，给定Policy $\pi$，State $s$, Action $a$，我们可以进行积分，获得$Q_{\pi }(s_t,a_t)$。这里需要注意，实际上$Q_{\pi }(s_t,a_t)$也是跟$s_{t+1},s_{t+2},\cdots$以及$a_{t+1},a_{t+2},\cdots$ 有关的，这个可以根据$U_t$的定义可得。但是由于积分将这些全部消除，就只剩下了观测值$s_t$和$a_t$。如果$\pi$不一样，积分得到的$Q_{\pi }(s_t,a_t)$也不一样。

上述定义是Policy based情形下的概念。即，我们是去学习策略$\pi$，最后根据策略$\pi$来做动作。

除了Policy based方法，还有一种value based方法，value based方法不是去学策略，而是去学最优动作-价值函数(Optimal Action-Value function，如下一节所介绍的)，最后基于Optimal Action-Value function来做决策。典型的算法就是Q-learning.

在value based方法中，Optimal Action-Value function就不带策略$\pi$，直接为$Q^{\ast }(s_t,a_t)$，在Q-learning中其实就是Q-table。

最优动作-价值函数(Optimal Action-Value function)

最优动作价值函数，Optimal action-Value function，定义如下：
$$\begin{array}{r}{Q}^{\ast }(s_t,a_t)=\underset{\pi }{\max }{Q}_{\pi }(s_t,a_t)\end{array}$$

最优动作价值函数与$\pi$无关，因为$\pi$已经被$\max$给消除了。Optimal action-Value function $Q^{\ast }(s_t,a_t)$可以用来对动作作评价。有了$Q^{\ast }(s_t,a_t)$，agent就可以利用$Q^{\ast }(s_t,a_t)$来做动作了。

具体来讲，在状态$s_t$下，下一步应该采取的动作可以由下式得到
$$a^{\ast }=\underset{a}{\mathrm{argmax}}{Q}^{\ast }(s,a)$$

另外，这里再次强调，$Q$值是对未来奖励总和的期望。

状态-价值函数(State-Value function)

状态-价值函数可以表示为
$$V_{\pi }(s_t)=\underset{a_t}{\max }{Q}^{\ast }(s_t,a_t)$$
也可以写为
$$V_{\pi }(s_t)={\mathbb{E}}_A[Q_{\pi }(s_t,A)]=\sum _a\pi (s_t,a)\cdot Q_{\pi }(s_t,a)$$

这个状态-价值函数(State-Value function)，给相当于之前介绍的动态规划中的$$f_k(s_k)$$。读者可以仔细进行对比。

Value based reinforcement learning 和policy based reinforcement learning

基于上述介绍，我们知道，要通过强化学习，最终能够指导agent做动作，可以有两大类方法：

1. 第一种：学习最优动作-价值函数(Optimal Action-Value function) $Q^{\ast }(s_t,a_t)$，根据下面标准指导agent做动作。即在状态$s_t$下，下一步应该采取的动作可以由下式得到
   $$a^{\ast }=\underset{a}{\mathrm{argmax}}{Q}^{\ast }(s,a)$$。简单来讲，就是用各种方法去近似$Q$ function。具体包括：

• Q-learning
• Sarsa
• DQN等。

2. 第二种：学习策略函数(policy function)$\pi (a|s)$，使其最大化状态-价值函数State-value function，策略函数$\pi (a|s)$实际上是一个概率分布，我们根据策略函数，在状态$s$下，根据概率分布$\pi (a|s)$即可得到下一步应该采取的动作$a$. 在这种方法下，我们最终其实可以同时得到策略函数$\pi (a|s)$以及状态-价值函数$V_{\pi }(s)$。具体包括：
   – Actor-Critic等。

强化学习算法分类

图片来自：https://spinningup.openai.com/en/latest/spinningup/rl_intro2.html#a-taxonomy-of-rl-algorithms

本文主要书里了一下与强化学习相关的马尔科夫链，马尔科夫决策过程以及动态规划之间的关系。这里做一个小的总结。

• 强化学习在数学上，常常被建模为一个马尔科夫决策过程；
• 马尔科夫决策过程可以使用动态规划算法求解；
• 动态规划是一大类算法框架。具体求解马尔科夫决策过程的算法主要包括两大类：值迭代和策略迭代。

参考资料

1. https://towardsdatascience.com/introduction-to-reinforcement-learning-markov-decision-process-44c533ebf8da

2. 强化学习之MDP马尔科夫决策过程，网址：https://stepneverstop.github.io/%E5%BC%BA%E5%8C%96%E5%AD%A6%E4%B9%A0%E4%B9%8BMDP%E9%A9%AC%E5%B0%94%E7%A7%91%E5%A4%AB%E5%86%B3%E7%AD%96%E8%BF%87%E7%A8%8B.html

3. https://zh.wikipedia.org/wiki/%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E9%93%BE

4. Lawler, Gregory F. Introduction to stochastic processes. Chapman and Hall/CRC, 2018.

5. https://towardsdatascience.com/introduction-to-reinforcement-learning-markov-decision-process-44c533ebf8da

6. Richard Bellman. On the theory of dynamic programming. Proceedings of the National
   Academy of Sciences of the United States of America, 38(8):716, 1952.

7. Richard Bellman. Dynamic programming. Science, 153(3731):34–37, 1966.

参考网址

1. 强化学习之MDP马尔科夫决策过程https://stepneverstop.github.io/%E5%BC%BA%E5%8C%96%E5%AD%A6%E4%B9%A0%E4%B9%8BMDP%E9%A9%AC%E5%B0%94%E7%A7%91%E5%A4%AB%E5%86%B3%E7%AD%96%E8%BF%87%E7%A8%8B.html
2. 强化学习的类别.https://spinningup.openai.com/en/latest/spinningup/rl_intro2.html#a-taxonomy-of-rl-algorithms
3. 强化学习之MDP马尔科夫决策过程. https://stepneverstop.github.io/%E5%BC%BA%E5%8C%96%E5%AD%A6%E4%B9%A0%E4%B9%8BMDP%E9%A9%AC%E5%B0%94%E7%A7%91%E5%A4%AB%E5%86%B3%E7%AD%96%E8%BF%87%E7%A8%8B.html
4. https://towardsdatascience.com/reinforcement-learning-markov-decision-process-part-2-96837c936ec3
5. 随机动态规划.https://en.wikipedia.org/wiki/Stochastic_dynamic_programming
6. 马尔科夫链.https://zh.wikipedia.org/wiki/%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E9%93%BE
7. 价值与贝尔曼方程.https://stepneverstop.github.io/%E4%BB%B7%E5%80%BC%E4%B8%8E%E8%B4%9D%E5%B0%94%E6%9B%BC%E6%96%B9%E7%A8%8B.html