泊松分布

泊松分布定义：如果随机事件A发生的概率是P，进行n次独立试验，恰巧发生了k次，则相应的概率可以用这样一个公式来计算：

在实际事例中，当一个事件以固定的平均速率出现时随机且独立地出现时，那么这个时间在单位时间（面积或体积等）内出现的次数或个数近似服从泊松分布。

如：

某医院平均每小时出生3个婴儿；（单位时间）

某公司平均每小时接到3.5个电话；（单位时间）

数学性质一：泊松分布是正态分布的一种微观视角，是正态分布的另一种面具

数学性质二：泊松分布的间隔是无记忆性的。

注意，不是说泊松分布是无记忆的，而是泊松分布的间隔无记忆。什么叫无记忆性呢？就是之前的情况对之后的情况没有影响。所以间隔的无记忆性就是指，前一间隔中随机事件是否发生对后一间隔中随机事件是否发生没有影响。

在城市大暴雨的案例中，如果去年发生了一次大暴雨，那今年发生大暴雨的概率会变成多少呢？按人类的直觉，大暴雨是平均50年发生一次，刚刚发生了一次，接下来一年就不会再发生大暴雨了，概率是0。

但是，这个看法是不对的。这又是概率反直觉的一个例子。今年发生了大暴雨与明年的大暴雨，相互没有影响，用概率论的术语就是“相互独立”。

一、理论知识

【先说说组合数C(n, k)】
C(n, k) = n!/(k!(n-k)!) 
一句话就是“n中选k”的所有可能数，详细的可以如下理解：
假设一份实验报告，有 n 个空格对应 n 次试验记录，每成功一次就对相应位置的空格打勾，如果你想要“定制”一份成功了 k 次的试验报告，就需要选其中 k 个空格打勾，这时候 C(n, k) 就代表所有的打勾方式。

【二项分布】
在 n 次 *独立* 试验中，事件 A 发生的总次数 X 的概率分布（且要求每次试验时 A 发生的概率 *相等*）。
【记号】一个随机变量 X 服从二项分布，通常用数学记号 X~B(n, p) 来表示。
其中，“实验次数 n”和“发生概率 p”决定了这个分布的所有特征。

【概率分布计算】
通过 n 和 p，我们可以计算出 X 取 0~n 中任何整数值 k 的概率：
P(X=k) = C(n,k)*(p^k)*[(1-p)^(n-k)]
其中，C(n, k) 就是上面说的组合数。
【例子】连续 10 次投硬币，正面朝上的次数 X=5 的概率：
P(X=5) = C(10, 5)*(0.5^5)[(1-0.5)^(10-5)]
= 252 * (0.5^10) ~ 0.246
（也就是文中说的大约 1/4）

【期望和方差】
二项分布的期望（均值）为 np，方差为 np(1-p)。（推导过程不难，不会也可以问问搜索引擎）

----------------
二项分布告诉我们：想要“期望 ”大，那就提升 n 和 p。

（限制了 p，就想法扩大 n）
* 而如果客观条件约束了胜算，只要“期望”收益为正，那就追求多次可重复。
例如，赌场，保险公司，风险投资……

大量可重复，概率的规律才有意义。
因为少量的“试验”次数，难以支撑那一点微小的概率优势；只有不断扩大 n，“运气”才会收敛到“期望”。

（限制了 n，就努力提升 p）
* 对难得的机会，最好事前充分地准备，提升成功概率，降低不确定性。
例如，错过等一年的高考，理想的职位面试，或者一些重要的仪式，甚至是“do or die”……

最怕的就是，当机会到来，只能遗憾地说：抱歉我还没准备好……
只有做足了准备，才能有底气的在成功之后说一句：这是我应得的！

【泊松分布与二项分布】
1）当二项分布的 n 很大而 p 很小时，泊松分布可作为二项分布的近似。
2）数学上，当 n 趋于无穷，而 np 的大小趋于一个（大于0）的稳定值  时（此时 p 无穷小），二项分布将“收敛”到泊松分布。
3）文中停车位的例子，其实理论上还是二项分布，但是由于 n=100 已经很大了，因此可以用泊松分布来近似这个二项分布。

泊松是离散型概率分布，分布特点：参数是单位时间（或单位面积）内随机事件的平均发生次数，当n>=20,p<=0.05时，就可以用泊松公式近似计算得出。

泊松分布中p必须很小，不然（math.exp(-λ)）=0，所有的概率都是0了

【泊松分布的期望和方差】
期望：μ =
方差：σ^2 =
# 对比一下“二项分布”，期望 μ = np 和方差 σ^2 = np(1-p)，发现没，当上面第（2）条满足时，对应的就是“泊松分布”的期望和方差！

【区别】
除了上述关系以外，泊松分布和二项分布还有一个很重要的区别，就是“试验成功次数 k”的取值范围不同。
* 对“二项分布”而言，试验“成功”的次数 k 只能取 0~n 之间，大于 n 的情况是不可能事件（概率为0）。
* 而对于“泊松分布”，成功次数 k 的取值 *没有上限*。也就是说，k 取任何一个非负的整数，对应的概率都是 *大于 0* 的（当然可能小到忽略不计）。

【泊松分布还能做什么？】
泊松分布适用于描述单位时间（或空间）内随机事件发生的次数。
例如，某奶茶店每分钟内到达的顾客人数（不考虑结伴而行），电话客服每小时接到的客户咨询数，机器出现的故障数，自然灾害发生的次数……

-------------------------------------------------------以上理论转自得到Cynthia

二、案例

1、停车场还有车位的概率是多大？---转自得到吴军《数学通识50讲》

    假如说公司门口有10个停车位，公司有100个上班的员工，每个员工早上8点之前开车来上班的概率是10%，他们每天什么时候来公司不仅是随机的，而且彼此无关，不存在两个人商量之后一起到的情况，而且也不存在头一天来晚了没抢到停车位，第二天找到的可能性。

    现在你是这家公司的新员工，早上8点整开车到了公司，请问停车场还有车位的概率是多大？

    在此案例中，首先我们利用泊松分布公式，计算一下k小于等于9的概率，我们需要把k=0,1,2,3...9全部代进那个公式中，一个个计算：

k	0	1	2	3	4	5	6	7	8	9
概率	0.00005	0.000454	0.00227	0.007567	0.018917	0.037833	0.063055	0.090079	0.112599	0.12511
累计概率	0.00005	0.000499	0.002769	0.010336	0.029253	0.067086	0.130141	0.220221	0.33282	0.45793

 

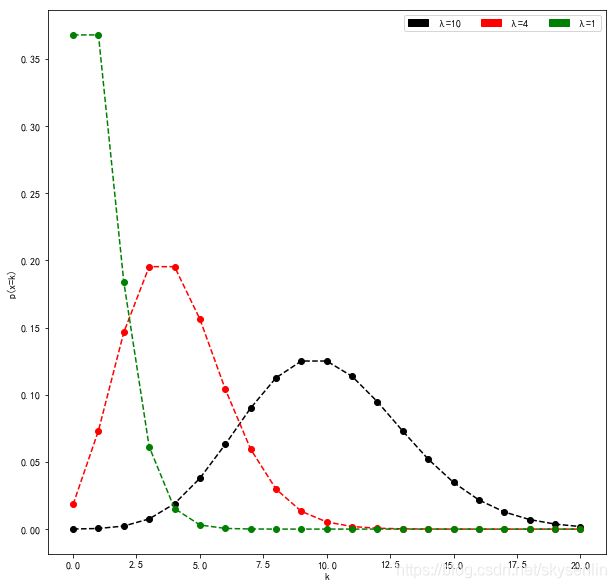
        从这个表格中可以看出，概率随着k的增加而逐渐增加，也就是说，8点之前，停车场没有车的概率小于有1辆车的概率，有1辆车的概率小于两辆车的概率，但到k=9 k=10这两个点，概率到达峰值，超过λ时，概率其实要往下走。这种现象对任何λ都是成立的。

        算完了k等于不同值的概率，我们就把表格中k=从0到9的各个概率加起来，就得到k小于等于9的总概率，我们称之为累积概率，放在了第三行。在这个问题中，它是0.46左右，也就是说你有将近一半的可能性能够获得车位。从表格的第三行累积概率的变化你可以看出，它一开始增长很慢，在k接近时就增长较快，再往后其实增长也很慢。

 

import math
import pandas
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
plt.rcParams['font.sans-serif'] = ['SimHei']  # 解决中文显示问题-设置字体为黑体
plt.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题

def f_a(num):
    """ num的阶乘  """
    factorial = 1
     
    # 查看数字是负数，0 或 正数
    if num < 0:
       print("抱歉，负数没有阶乘")
    elif num == 0:
        factorial=1
#       print("0 的阶乘为 1")
    else:
       for i in range(1,num + 1):
           factorial = factorial*i
    return factorial


def Poisson(l,k):
    """
    l:λ
    k:泊松分布中某事件发生的次数
    """
    p=(math.pow(l,k)*math.exp(-l))/f_a(k)
    return p
    
#在此案例中，λ=n*p=10时
λ_10=100*0.1

k_list=[]
one_probability=[] 
cumul_probability=[]
sum_pro=0
for i in range(21):
    one_pro=Poisson(λ_10,i)
    sum_pro+=one_pro
    k_list.append(i)
    one_probability.append(one_pro)
    cumul_probability.append(sum_pro)
    
factorial_10=pandas.DataFrame()
factorial_10['k']=k_list
factorial_10['概率']=one_probability
factorial_10['累计概率']=cumul_probability
#在此案例中，λ=n*p=4时
λ_4=100*0.04

k_list=[]
one_probability=[] 
cumul_probability=[]
sum_pro=0
for i in range(21):
    one_pro=Poisson(λ_4,i)
    sum_pro+=one_pro
    k_list.append(i)
    one_probability.append(one_pro)
    cumul_probability.append(sum_pro)
    
factorial_4=pandas.DataFrame()
factorial_4['k']=k_list
factorial_4['概率']=one_probability
factorial_4['累计概率']=cumul_probability

#在此案例中，λ=n*p=1时
λ_1=100*0.01

k_list=[]
one_probability=[] 
cumul_probability=[]
sum_pro=0
for i in range(21):
    one_pro=Poisson(λ_1,i)
    sum_pro+=one_pro
    k_list.append(i)
    one_probability.append(one_pro)
    cumul_probability.append(sum_pro)
    
factorial_1=pandas.DataFrame()
factorial_1['k']=k_list
factorial_1['概率']=one_probability
factorial_1['累计概率']=cumul_probability

color = ['black', 'red', 'green']  #指定泊松分布的颜色

#我试过这里不能直接生成legend，解决方法就是自己定义，创建legend
labels = ['λ=10', 'λ=4', 'λ=1']  #legend标签列表，上面的color即是颜色列表
#用label和color列表生成mpatches.Patch对象，它将作为句柄来生成legend
patches = [mpatches.Patch(color=color[i], label="{:s}".format(labels[i]) ) for i in range(len(color)) ] 

ax=factorial_10[['概率']].plot(style = 'k--o',legend = 'λ=10',figsize=(10,10))
factorial_4[['概率']].plot(style = 'r--o',legend = 'λ=4',ax=ax)
factorial_1[['概率']].plot(style = 'g--o',legend = 'λ=1',ax=ax)
#下面一行中bbox_to_anchor指定了legend的位置
ax.legend(handles=patches, ncol=3) #生成legend , bbox_to_anchor=(0.95,1.12)
plt.xlabel('k')  # x轴标签
plt.ylabel('p(x=k)') # y轴标签
plt.show()

 泊松分布可以直接掉stats里的函数生成

import math
import pandas
import numpy as np
from scipy import stats
n=100
rated=0.1
lamda=n*rated
y=stats.poisson.pmf(np.arange(11),mu=lamda)
pmf_data=pandas.DataFrame()
pmf_data['概率']=y
pmf_data['累计概率']=pmf_data['概率'].cumsum()

在此案例基础上，我们可以提出以下问题

a、p=10%值不变，若公司人员增加到200人，停车位数量增加到20个，其他条件不变，8点到有停车位的概率是多少？

k	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
概率	0.00000	0.00000	0.00000	0.00000	0.00001	0.00005	0.000183	0.000523	0.001309	0.002908	0.005816	0.010575	0.017625	0.027116	0.038737	0.051649	0.064561	0.075954	0.084394	0.088835	0.088835
累计概率	0.00000	0.00000	0.00000	0.00000	0.00002	0.00007	0.000255	0.000779	0.002087	0.004995	0.010812	0.021387	0.039012	0.066128	0.104864	0.156513	0.221074	0.297028	0.381422	0.470257	0.559093

p=10%，N=500，λ=50，有车位的概率为48.12%

p=10%，N=200，λ=20，有车位的概率为47.03%

 p=10%，N=100，λ=10，有车位的概率为45.79%

结论：P值不变的基础上，想要增加概率，就增加N，N不变的基础上，想要增加概率，增加P。N 和 P都不变的基础上，增加冗余量。

应对随机性，需要的冗余比你想的要大。

在现实生活中，电话公司通常要多准备一些线路，以免大家打电话的时候总是占线。根据前面的分析我们得知，如果电话公司准备的线路数量正好是λ，也就是打电话人数的平均值，那么有一半的时间大家在打电话时会遇到占线的情况，这个比例是非常高的，你肯定会抱怨不止。

#p=10%值不变，若公司人员增加到200人
λ_p10=200*0.1

k_list=[]
one_probability=[] 
cumul_probability=[]
sum_pro=0
for i in range(41):
    one_pro=Poisson(λ_p10,i)
    sum_pro+=one_pro
    k_list.append(i)
    one_probability.append(one_pro)
    cumul_probability.append(sum_pro)
    
factorial_p10=pandas.DataFrame()
factorial_p10['k']=k_list
factorial_p10['概率']=one_probability
factorial_p10['累计概率']=cumul_probability

#p=20%，公司人数不变
λ_p20=100*0.2

k_list=[]
one_probability=[] 
cumul_probability=[]
sum_pro=0
for i in range(41):
    one_pro=Poisson(λ_p20,i)
    sum_pro+=one_pro
    k_list.append(i)
    one_probability.append(one_pro)
    cumul_probability.append(sum_pro)
    
factorial_p20=pandas.DataFrame()
factorial_p20['k']=k_list
factorial_p20['概率']=one_probability
factorial_p20['累计概率']=cumul_probability

color = ['red', 'green']  #指定泊松分布的颜色

#我试过这里不能直接生成legend，解决方法就是自己定义，创建legend
labels = ['p=10% n=200', 'p=20% n=100']  #legend标签列表，上面的color即是颜色列表
#用label和color列表生成mpatches.Patch对象，它将作为句柄来生成legend
patches = [mpatches.Patch(color=color[i], label="{:s}".format(labels[i]) ) for i in range(len(color)) ] 

ax=factorial_p10[['概率']].plot(style = '--o',color='red',figsize=(10,10))
factorial_p20[['概率']].plot(style = '--o',color='green',ax=ax)

#下面一行中bbox_to_anchor指定了legend的位置
ax.legend(handles=patches, ncol=2) #生成legend , bbox_to_anchor=(0.95,1.12)
plt.xlabel('k')  # x轴标签
plt.ylabel('p(x=k)') # y轴标签
plt.show()

 

2、航空公司该售多少票？

航空公司售票，1个飞机有380个座位，平均有90%的人来，如果航空公司售卖400张机票，那么有多大的概率会有超过380的人来？

期望：λ=380*90%=360

标准差：=

正负1倍标准偏差的概率 =68.3% 正负2倍标准偏差的概率 =95.5% 正负3倍标准偏差的概率 =99.7% 

380>(λ+3=378)   =>> (100%-99.7%)/2=0.15%

大概有0.15%即千分之一的概率会有超过380的人来。

3、厕所排队时间

参考网址：https://blog.csdn.net/a493823882/article/details/78175824

https://www.jianshu.com/p/e3942d47030c

https://www.bilibili.com/video/BV1cT4y1g7gj?from=search&seid=10568284721091945198

如果每场电影结束之后会有20个人想上厕所，并且都在10分钟内上完，平均每个人上厕所时间是2分钟，需要安装几个蹲位？

1个坑可以让几个人用？10分钟/2分钟=5人

需要几个坑位：20人/5人=4（个）

λ=20

①已知某车站等候人数服从泊松分布，λ=4.5，求刚好两个人在候车的概率。

解：该题单位为每个车站，带入公式已知p（x==2）=4.5^2/2*e^(-4.5)≈0.112

②某医院平均每小时出生3个婴儿，则接下来两个小时没有婴儿出生的概率是多少？

解：该题单位为每小时，代入公式p（N(2)==0）=(3*2)^0*e^(-3*2)/2≈0.0025

③某医院平均每小时出生3个婴儿，接下来15分钟有婴儿出生的概率是多少？

4、二战空袭伦敦期间，炸弹是集群式分布还是随机分布？---转自书《成为数据分析师--6步练就数据思维》

案例背景知识：

在第二次世界大战期间。德军生产 出了一款叫作V-2的威力巨大的新型火箭弹，以威胁伦敦市民的安全。在接下来的几 个月里，至少有3 172枚V-2火箭弹遍布在各个同盟国国家中，其中的1 358枚投向 伦敦地面，导致了约7 250名军人和平民的死亡。

在空袭伦敦期间，许多观察家坚称炸弹打到的各点是集群式分布的。英国人很 想知道，德国人是有目标的炸弹攻击还是只是随机攻击。英国人认为，如果德国人 只是随机攻击目标，那么部署在遍布全国的各种安全装备能够很好地保护国家，但 如果德国人能够进行有目标的轰炸，那么英国人面临的是一个更强有力的对手。因 此，在全国范围内部署的安全装备可能还不足以保护国家的安全。英国政府雇用了 统计学家克拉克（R.D.Clarke）来解决这个问题。克拉克基于他对之前的发现或已存在的知识的回顾，实施了一个简单的统计分析。

克拉克意识到，泊松分布（Poisson distribution）可以用于分析这些炸弹的 分布。如果事情以一个已知的平均概率发生，泊松分布就会解释这些事情发生在某 段固定时期、固定区域或固定体积内的可能性。为了具体了解泊松分布，我们必须 知道的一件事情就是事件发生的平均概率。如果炸弹是随机落下的，那么轰炸任何特定小区域的炸弹的数量会遵循泊松分布。例如，如果炸弹的平均轰炸数是每个区 域1枚炸弹，那么只需把这些数字填写到泊松公式里，我们就可以轻松又精准地计算 出没有炸弹轰炸的可能性，如1枚炸弹轰炸的可能性、2枚炸弹轰炸的可能性、3枚 炸弹轰炸的可能性、4枚炸弹轰炸的可能性和更多枚炸弹轰炸的可能性。

为了测算某一特定小区域可能受到多少枚炸弹的轰炸，克拉克把南伦敦划分为 576个方块，每个方块为0.25平方公里大小，然后对飞过的炸弹按照0、1、2、3等 进行计数。如果轰炸完全是随机的，那么每一个方块被0、1、2、3等炸弹轰炸的可 能性将符合泊松分布。事实上，结果数据和泊松分布匹配得非常好，因此，它不支 持集群分布的假设。克拉克的结论让英国人松了一口气。让人感到幸运的是，在V-2 火箭弹造成更大破坏之前，德国在1945年投降了。尽管德国没能让导弹有效制导， 但是火箭却成了美国太空计划的技术基础。

1）计算每个方块的平均轰炸数

λ=总轰炸数/总方格数

2）利用泊松分布，计算每个方格1个炸弹轰炸的可能性、2个炸弹轰炸的可能性、3个炸弹轰炸的可能性...

p(x=0)

p(x=1)

p(x=2)

3）对飞过的炸弹按照0、1、2、3等进行计算

actual_0=未轰炸方格数/总方格数

actual_1=轰炸过1次的方格数/总方格数

actual_2=轰炸过2次的方格数/总方格数

actual_3=轰炸过3次的方格数/总方格数

4）对比2）和3）是否匹配，比如actual_0和p(x=0)在概率是否一致，actual_1和p(x=1)在概率上是否一致

每个网格被轰炸次数	泊松概率	实际概率	实际概率计算过程
0	0.02	0.10	未轰炸方格数/总方格数
1	0.07	0.12	轰炸过1次的方格数/总方格数
2	0.15	0.23	轰炸过2次的方格数/总方格数
3	0.20	0.23	轰炸过3次的方格数/总方格数
4	0.20	0.30	轰炸过4次的方格数/总方格数
5	0.16	0.17	轰炸过5次的方格数/总方格数
6	0.10	0.12	轰炸过6次的方格数/总方格数
7	0.06	0.14	轰炸过7次的方格数/总方格数
8	0.03	0.13	轰炸过8次的方格数/总方格数
9	0.01	0.05	轰炸过9次的方格数/总方格数
10	0.01	0.01	轰炸过10次的方格数/总方格数
11	0.00	0.00	轰炸过11次的方格数/总方格数
12	0.00	0.01	轰炸过12次的方格数/总方格数
13	0.00	0.00	轰炸过13次的方格数/总方格数
14	0.00	0.01	轰炸过14次的方格数/总方格数
15	0.00	0.01	轰炸过15次的方格数/总方格数
16	0.00	0.01	轰炸过16次的方格数/总方格数
17	0.00	0.01	轰炸过17次的方格数/总方格数

5）KS-检验（Kolmogorov-Smirnov test） -- 检验数据是否符合某种分布

参考网址：https://www.cnblogs.com/arkenstone/p/5496761.html

https://www.cnblogs.com/webRobot/p/9114411.html

KS统计量来检验这两组样本分布是否有显著差异

两条曲线算的是累计概率

计算各阶段的差值

最后算差值的最大值

import numpy as np
from scipy.stats import ks_2samp
poisson_data=np.array([0.01831564,0.07326256,0.14652511,0.19536681,0.19536681,0.15629345,0.10419563,0.05954036,0.02977018,0.01323119,0.00529248,0.00192454,0.00064151,0.00019739,0.00005640,0.00001504,0.00000376,0.00000088])
actual_data=np.array([0.09831564,0.12326256,0.22652511,0.22536681,0.29536681,0.16629345,0.12419563,0.13954036,0.12977018,0.05323119,0.01129248,0.00492454,0.00664151,0.00319739,0.01005640,0.01001504,0.00500376,0.00800088])
ks_2samp(poisson_data,actual_data)

最终返回的结果，p-value=0.13，比指定的显著水平（假设为5%）大，则我们可以认为实际轰炸和泊松分布相同，而泊松分布属于随机事件发生次数和概率的一种分布，故得出德军轰炸属于随机事件，不支持集中分布的假设。