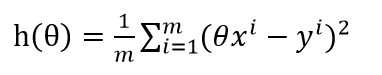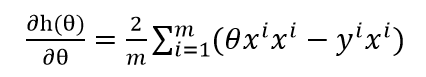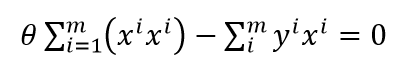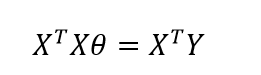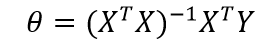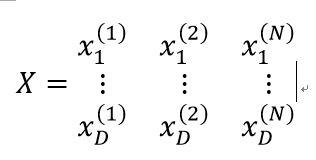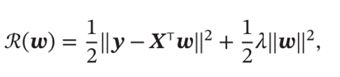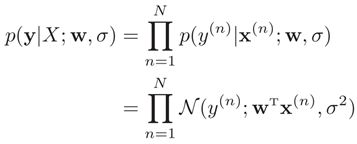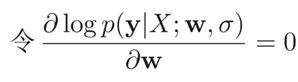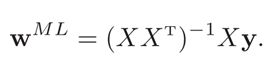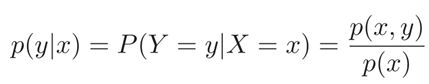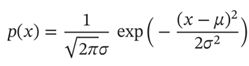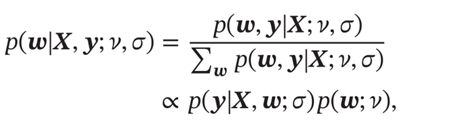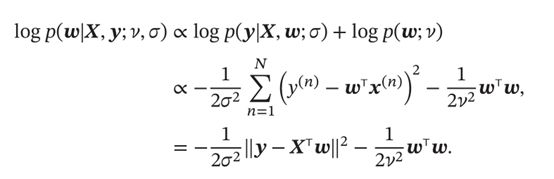线性回归--经验最小化，结构最小化，最大似然估计，最大后验估计

自己开发了一个股票智能分析软件，功能很强大，需要的点击下面的链接获取：

https://www.cnblogs.com/bclshuai/p/11380657.html

1.1  线性回归

1.1.1         原理简介

线性回归是对一次函数的拟合y=θ1x1+……+θixi+b，其中xi为自变量，每一个输入向量（x1……xi）就是一个特征向量，可以用最小二乘法推导出参数矩阵计算公式，也可以用迭代的方法求出参数值。设定损失函数，一般为误差均方根（RMSE），或者直接用均方误差，对参数求偏导数，偏导数为0时，就是极值点，求出使得损失函数值最小的参数，即为最优解。

    式（5-1）

对 求导，可以得出

  式（5-2）

要使得 的值最小，必须使导数为0，式（5-2）等于0的

    （5-3）

转换成矩阵的形式

              （5-4）

         （5-5）

 

1.1.2         经验风险最小化

经验风险最小化就是采用最小二乘法，使得损失函数的值最小。XTX必须存在逆矩阵，也就是XTX是满秩，X的行向量之间线性不相关。如果XTX不可逆，那么可以用主成分分析法消除相关性，再使用最小二乘法。或者用梯度下降法，先初始化参数，然后通过迭代求出参数。

1.1.3         结构风险最小化

最小二乘法的要求各个行向量之间相互独立，这样可以保证XTX是可逆的。X矩阵如下所示，最后还有一行全1的行。行向量X1……XD如果是线性相关的，也就是输入向量之间相关性很强，在求逆矩阵XTX时，数据集一个小的扰动就会导致逆矩阵发生大的改变，导致计算变的很不稳定，这种现象叫做行向量之间具有多重共线性。

 

 

 

多重共线性，在线性回归模型时，存在这样一种假设，即各个行向量之间不存在很强的关系。如果行向量之间存在很强的线性相关关系，就认为数据之间存在共线性问题。共线性会导致回归参数不稳定，即增加或删除一个样本点或特征，回归系数的估计值会发生很大变化。 这是因为某些解释变量之间存在高度相关的线性关系，XTX会接近于奇异矩阵，即使可以计算出其逆矩阵，逆矩阵对角线上的元素也会很大，这就意味着参数估计的标准误差较大，参数估计值的精度较低，这样，数据中的一个微小的变动都会导致回归系数的估计值发生很大变化。

为了解决这个问题，采用岭回归方法，即对角线元素都加上一个常量λ，这样各个行向量之间的线性相关性就会降低。行列式不为0，就可以去除逆矩阵。目标函数是

 

 

 

最优参数的迭代公式为

 

 

 

1.1.4         最大似然估计

参考文献：https://blog.csdn.net/u011508640/article/details/72815981

机器学习任务有两类，一类是上述未知函数拟合，另一类是条件概率分布服从未知的分布。线性回归还可以通过建模条件概率分布的角度来进行参数估计。函数拟合是使目标函数的值最小来求得参数。而似然估计则是使得事件出现的概率最大，也就是似然函数的值最大，来求得参数。参数w在训练集D上的似然函数（Likelihood）为

 

 

 

找到一组参数w使得似然函数p(y|X;w,σ)最大

 

 

 

求出的参数如下所示，由此可见，最大似然估计和最小二乘法的解相同。

 

 

 

（1）   概率统计

概率是已知模型和参数，推数据。统计是已知数据，推模型和参数。

（2）条件概率

对于离散随机向量(X,Y )，已知X = x的条件下，随机变量Y = y的条件概率为：

 

 

 

 

（3）贝叶斯公式

如下所示，举例A是汽车被砸，B是汽车警报响了。P(A|B)汽车警报响了，是汽车被砸了引起的概率。P(B|A)就是汽车被砸A条件下， 触发警报响了B的概率，P(A)就是汽车被砸的概率，P(B)是警报响的概率。

P(A|B)=P(B|A)P(A)/P(B) 

（4）似然函数

P(x|θ)

输入有两个：x表示某一个具体的数据；θ表示模型的参数。

如果θ是已知确定的，x是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点x，其出现概率是多少。

如果x是已知确定的，θ是变量，这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数，出现x这个样本点的概率是多少。

（4）最大似然估计（Maximum Likelihood Estimation）

最大似然估计就是求出现x样本点的概率最大时参数的值。

假设有一个造币厂生产某种硬币，现在我们拿到了一枚这种硬币，想试试这硬币是不是均匀的。即想知道抛这枚硬币，正面出现的概率（记为θ）。于是我们拿这枚硬币抛了10次，得到的数据（x0）是：反正正正正反正正正反。我们想求的正面概率θ是模型参数，而抛硬币模型我们可以假设是 二项分布。似然函数为:

f(x0,θ)=(1−θ)×θ×θ×θ×θ×(1−θ)×θ×θ×θ×(1−θ)=θ7(1−θ)3=f(θ)

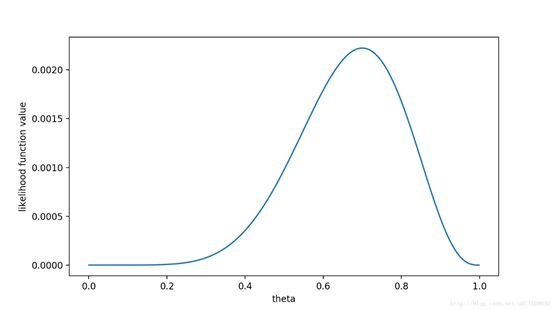
画出f(θ)的图像

 

 

 

可以看出，在θ=0.7时，似然函数取得最大值。这样，我们已经完成了对θ的最大似然估计。即，抛10次硬币，发现7次硬币正面向上，最大似然估计认为正面向上的概率是0.7。

1.1.5         最大后验估计（maximum a posteriori probability estimate）

最大似然函数的缺陷是训练数据较小时参数估计不准，只做了10次投硬币，就得出这个概率为0.7是不被信任的。根据人们的经验，θ一般为0.5，假设P(θ)为均值u=0.5，方差σ=0.1的高斯函数。高斯函数公如下：

 

 

 

给目标函数乘以一个先验函数得到的目标函数是P(x0|θ)P(θ)= θ7(1−θ)3*exp(-(x-u)2/2σ2)。使得这个函数值最大的参数估计叫做最大后验估计。根据贝叶斯公式，后验估计和似然估计之间的关系为：

p（x0|θ）=p（θ| x0）*p（θ）/p(x0)

后验                似然      先验 

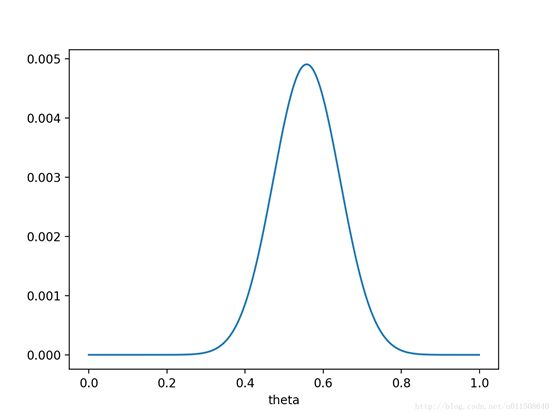
p(x0)是指1000次实验中，出现反正正正正反正正正反次数n/1000。这是一个常量值，求导之后常数值不影响，所以求使p（x0|θ）的最大的参数，转化为求出使得函数p（θ| x0）*p（θ）最大的参数，这就是后验估计。在本实例中就是求出使得P(x0|θ)P(θ)= θ7(1−θ)3*exp(-(x-0.5)2/2*0.12)最大的参数。画出函数曲线如下图所示

 

 

 

θθ取值已向左偏移，不再是0.7。实际上，在θ=0.558θ=0.558时函数取得了最大值。即，用最大后验概率估计，得到θ=0.558。

上面只是结合实例讲解，后验估计涉及多个参数，通用公式推导

 

两边求对数得到公式

 

由此可见，最大后验估计和等价于平方损失的结构风险最小化的，正则化系数为

σ2/v2

1.1.6         总结

(1)  MAP最大后验估计就是似然估计MLE多了一个先验概率P(θ)。或者，也可以反过来，认为MLE是把先验概率P(θ)认为等于1的均匀分布。

p（x0|θ）=p（θ| x0）*p（θ）/p(x0)

后验     似然      先验 

(2)  最大似然估计和最小二乘法的解相同，最大后验估计和等价于平方损失的结构风险最小化的，正则化系数为σ2/v2

	无先验	引入先验
平方误差	经验风险最小化	结构风险最小化
概率	最大似然估计	最大后验估计
参数估计