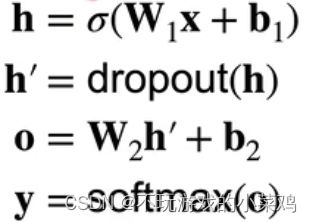0901权重衰退

处理过拟合

控制模型容量：1.模型参数变少  2.模型参数范围变小

权重衰退：为处理过拟合的用得比较多的方法

最理想的状态是达到0.

1/2是为了求导后计算方便（系数为1了）

前面是严格限制了范围，故为硬性限制，而此处是增加了一个罚项，相比较则为柔性限制

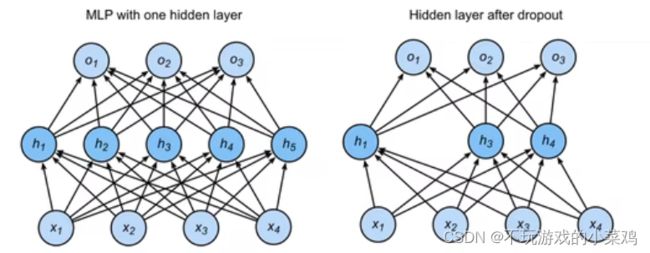
Dropout -- 丢弃法

（鲁棒是Robust的音译,也就是健壮、强壮、坚定、粗野的意思。鲁棒性(robustness)就是系统的健壮性。）

加噪音不改变期望

丢弃法：一定概率变0，一定概率变大

由此公式可得到需要的E[x'] = x

h为第一个隐藏层的输出

推理中的丢弃法

丢弃概率多取0.5， 0.9， 0.1

Dropout是一个正则项，对模型更新不明显，对。 求梯度对称

 dropout 随机丢弃，精度高，随机性让模型更稳定

只是在训练中把神经元丢弃，预测中神经元不丢弃

代码实现
权重衰减
权重衰减是最广泛使用的正则化的技术之一

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l

n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)

初始化模型参数

def init_params():
    w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
    b = torch.zeros(1, requires_grad=True)
    return [w, b]

定义L2范数惩罚

def l2_penalty(w):
    return torch.sum(w.pow(2)) / 2

定义训练代码实现

def train(lambd):
    w, b = init_params() #初始化
    net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss #线性回归 平方损失函数
    num_epochs, lr = 100, 0.003
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test']) #动画效果
    for epoch in range(num_epochs):
        for X, y in train_iter:
            #with torch.enable_grad():
            l = loss(net(X), y) + lambd * l2_penalty(w)
            l.sum().backward()
            d2l.sgd([w, b], lr, batch_size)
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                     d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数是：', torch.norm(w).item())

忽略正则化直接训练

train(lambd=0) #无惩罚
1
结果：w的L2范数是： 13.713445663452148

使用权重衰减

train(lambd=3)
1
结果：w的L2范数是： 0.3729381859302521

简洁实现

def train_concise(wd):
    net = nn.Sequential(nn.Linear(num_inputs, 1))
    for param in net.parameters():
        param.data.normal_()
    loss = nn.MSELoss()
    num_epochs, lr = 100, 0.003
    trainer = torch.optim.SGD([{
        "params": net[0].weight,
        'weight_decay': wd}, {
            "params": net[0].bias}], lr=lr)
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    for epoch in range(num_epochs):
        for X, y in train_iter:
            with torch.enable_grad():
                trainer.zero_grad()
                l = loss(net(X), y)
            l.backward()
            trainer.step()
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                     d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数：', net[0].weight.norm().item())

train_concise(0)
1
结果：w的L2范数： 12.6707124710083

train_concise(3)
1
结果：w的L2范数： 0.350588858127594

pycharm完整代码：

import torch
import torch.nn as nn
import numpy as np
import sys
sys.path.append(".")
import d2lzh_pytorch as d2l
import sys
from matplotlib import pyplot as plt

"""
生成一个人工数据集，还是一个线性回归的问题，
偏差0.05+权重0.01乘以随机的输入x然后+噪音，均值为0，方差为0.01的正态分布
"""
n_train, n_test, num_inputs = 20, 100, 200
# 训练数据集越小，越容易过拟合。训练数据集为20，测试数据集为100，特征的纬度选择200.
# 数据越小，模型越简单，过拟合越容易发生

true_w, true_b = torch.ones(num_inputs, 1) * 0.01, 0.05
# 真实的权重就是0.01*全1的一个向量，偏差b为0.05

"""
读取一个人工的数据集
"""
features = torch.randn((n_train + n_test, num_inputs))  # 特征
labels = torch.matmul(features, true_w) + true_b  # 样本数
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)
train_features, test_features = features[:n_train, :], features[n_train:, :]
train_labels, test_labels = labels[:n_train], labels[n_train:]

"""
初始化模型，该函数为每个参数都附上梯度
"""


def init_params():
    w = torch.randn((num_inputs, 1), requires_grad=True)
    b = torch.zeros(1, requires_grad=True)
    return [w, b]


"""
定义L2范数惩罚，只惩罚模型的权重参数
"""


def l2_penalty(w):
    return (w ** 2).sum() / 2


"""
定义训练和测试模型
"""
batch_size, num_epochs, lr = 1, 100, 0.003
net, loss = d2l.linreg, d2l.squared_loss
dataset = torch.utils.data.TensorDataset(train_features, train_labels)
train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle=True)


def fit_and_plot(lambd):
    w, b = init_params()
    train_ls, test_ls = [], []
    for _ in range(num_epochs):
        for X, y in train_iter:
            # 添加了L2范数惩罚项
            l = loss(net(X, w, b), y) + lambd * l2_penalty(w)
            l = l.sum()
            if w.grad is not None:
                w.grad.data.zero_()
                b.grad.data.zero_()
            l.backward()
            d2l.sgd([w, b], lr, batch_size)
        train_ls.append(loss(net(train_features, w, b), train_labels).mean().item())
        test_ls.append(loss(net(test_features, w, b), test_labels).mean().item())
    d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
                 range(1, num_epochs + 1), test_ls, ['train', 'test'])
    print('L2 norm of w:', w.norm().item())

    fit_and_plot(lambd=0)
    plt.show()