欠拟合与过拟合及其解决方法
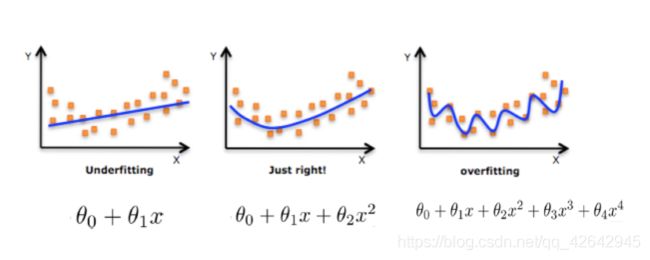
下面三张图表示的是拟合的函数和训练集的关系：
- 第一张图拟合的函数和训练集误差较大，这种情况称为
欠拟合 - 第二张图拟合的函数和训练集误差较小，这种情况称为
合适拟合 - 第三张图拟合的函数完美的匹配训练集数据，这种情况称为
过拟合
一、欠拟合（Underfitting）
模型在训练数据上不能获得很好的拟合，并且在测试数据集上也不能很好的拟合数据，这种现象称为欠拟合，即高偏差（high bias）。(模型过于简单)
原因：模型不够复杂、拟合函数的能力不足，学习到的有用特征太少，导致拟合的函数无法满足训练集。
二、过拟合（Overfitting）
模型在训练数据上能够获得很好的拟合，但是在测试数据集上却不能很好的拟合数据，这种现象称为过拟合，即高方差（high variance）。(模型过于复杂，泛化能力差)
原因：
- 对于数据集来说，模型过于复杂、拟合能力过强，学习了训练数据中的噪声和训练样例中没有代表性的特征，导致模型学习到的特征数过多。
- 训练数据不足，即训练数据无法对整个数据的分布进行估计。
1.交叉验证（cross-validation）
先解释一下bias和variance的概念。模型的Error = Bias + Variance，Error反映的是整个模型的准确度，Bias反映的是模型在样本上的输出与真实值之间的误差，即模型本身的精准度，Variance反映的是模型每一次输出结果与模型输出期望之间的误差，即模型的稳定性。
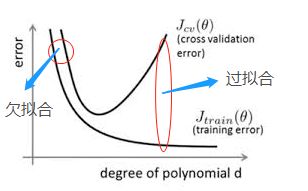
在缺少有效预防欠拟合和过拟合措施的情况下，随着模型拟合能力的增强，错误率在训练集上逐渐减小，而在验证集上先减小后增大；当两者的误差率都较大时，处于欠拟合（high bias, low variance）；当验证集误差率达到最低点时，说明拟合效果最好，由最低点增大时，处于过拟合（high variance, low bias）。下图的横坐标用拟合函数多项式的阶数笼统地表征模型拟合能力：
2.偏差（bias）和方差（variance）
偏差（bias），是不同数据集在特定模型上预测值的期望与实际值之间的差值。如果平均预测值与实际值相差甚远，则偏差较高。高偏差导致算法无法正确表示输入和输出变量之间的相关关系。当模型具有较高的偏差时，则表示该模型过于简单，无法捕获数据的复杂性，因此无法拟合数据。
方差（variance），指的是不同数据集在特定模型上的预测值的方差。当模型在训练后的数据集上表现良好但在未训练的数据集（例如测试数据集或验证数据集）上表现不佳时，就会发生方差。 方差反映了预测值与实际值之间的分散程度。高方差会导致过度拟合，这表明该算法对训练数据中存在的随机噪声也进行了建模。当模型具有较高的方差时，该模型将变得非常复杂，并将“完美拟合”训练集的数据点。 当高方差模型遇到尚未学习的其他数据点时，就无法做出正确的预测。
上图表示了偏差和误差，其中蓝色点表示我们的预测值，红色点表示我们的真实值。可以看到，偏差越高，预测值离真实值越远；方差越高，预测值越分散。
用
表示我们要预测的值（样本真实值），
表示我们的自变量。考虑到样本数据其实是采样，并不是真实值，假设真实模型是
，则有这样的关系：
，其中
表示噪音，服从均值为0的正态分布，即
。用
来表示我们的模型（即拟合函数），则我们的预测值为
，则在点
处的平方误差的期望为：
![Err(x)=E\left [ (Y-\hat{f}(x))^{2} \right ]=E\left [ (\epsilon +f(x)-\hat{f}(x))^{2} \right ]](http://img.e-com-net.com/image/info8/ec8baed16a9d456a81d906447a834c70.gif){kind=small}
![=E\left [f(x)^{2} \right ]+E[\hat{f}(x)^{2}]+E(\epsilon ^{2})-2E[ f(x)]E [\hat{f}(x)]-2E(\epsilon)E [f(x)]-2E [\epsilon ]E[\hat{f}(x)]](http://img.e-com-net.com/image/info8/9fac8934ce1a484bad03be2dc7717c0b.gif){kind=small}
![=f(x)^{2}+ ( E[ \hat{f}(x) ] )^{2}+Var[\hat{f}(x) ]-2f(x)E[ \hat{f}(x)]+Var\left [ \epsilon \right ]+E(\epsilon )](http://img.e-com-net.com/image/info8/3a3e767c63e94f4b85ff9c5aaf309cd3.gif){kind=small}
![=\left ( E\left [ \hat{f}(x) \right ]-f(x) \right )^{2}+E\left [ (\hat{f}(x)-E[ \hat{f}(x) ]) ^{2}\right ]+\sigma_{e}^{2}](http://img.e-com-net.com/image/info8/a6dca9fa6bbb4c3fb78f39827dfc48ca.gif){kind=small}
注意：
，
，三者独立，且不是变量，是固定值。所以![E[f(x)]=f(x)](http://img.e-com-net.com/image/info8/cddb8d6e3aa34c188a2599e426abc66d.gif){kind=small}
，![E[f(x)^{2}]=f(x)^{2}](http://img.e-com-net.com/image/info8/ed027f367f9d452d9be75da6ae9e5426.gif){kind=small}
。
即误差的期望值 = 预测值相对真实值的偏差的平方 + 模型预测值的方差 + 噪音的方差
上式中的第三项，为不可减少的误差，是真实模型和样本值的关系中的噪声项，任何模型都无法从根本上减少噪声项。给定真实模型和无穷大数据进行校准，理论上可以将偏差项和方差项都减少到0。但是，在模型和有限数据不完善的现实情况下，需要在最小化偏差和最小化方差之间进行权衡。
三、解决方法
欠拟合解决方法
1.模型复杂化
- 添加多项式特征。给模型添加高次项（二次项、三次项及以上）使模型泛化能力更强，例如上面前三张图的例子，还有增加决策树的深度，增加神经网络的隐藏层数和隐藏单元数。
- 使用更复杂的算法或模型。例如用神经网络来代替线性回归，用随机森林来代替决策树。
2.增加特征
添加强表达能力的特征。有时候模型出现欠拟合是因为特征项不够导致的，可以添加其他特征项来很好地解决。例如，“组合”、“泛化”、“相关性”三类特征是特征添加的重要手段，无论在什么场景，都可以照葫芦画瓢，总会得到意想不到的效果。除上面的特征之外，“上下文特征”、“平台特征”等等，都可以作为特征添加的首选项。
3.减小正则化参数
减小正则化参数。正则化是用来防止模型过拟合的，如果模型现在不是过拟合而是欠拟合，那么就可以考虑降低正则化参数λ或者直接去除正则化项。
4.调整参数和超参数
- 超参数（在开始学习过程之前设置值的参数，而不是通过训练得到的参数数据）包括：
- 神经网络：学习率、学习衰减率、隐藏层数、隐藏层的单元数、Adam优化算法中的β1和β2参数、batch_size数值等
- 其他算法：随机森林的树数量，k-means中的cluster数，正则化参数λ等
过拟合解决方法
1.数据清洗
产生过拟合的原因可能是由于数据噪声干扰过多导致的，所以可以选择重新清洗数据。
2.数据集扩增（增加训练数据）
在数据挖掘领域流行着这样的一句话，“有时候往往拥有更多的数据胜过一个好的模型”。因为在使用训练数据训练模型，通过这个模型对将来的数据进行拟合，而在这之间有一个假设便是，训练数据与将来的数据是独立同分布的。即使用当前的训练数据来对将来的数据进行估计与模拟，而更多的数据往往估计与模拟地更准确。因此，更多的数据有时候更优秀。但是往往条件有限，如人力物力财力的不足，而不能收集到更多的数据，如在进行分类的任务中，需要对数据进行打标，并且很多情况下都是人工的进行打标，因此一旦需要打标的数据量过多，就会导致效率低下以及可能出错的情况。所以，往往在这时候，需要采取一些计算的方式与策略在已有的数据集上进行手脚，以得到更多的数据。
通俗得讲，数据集扩增即需要得到更多的符合要求的数据，即和已有的数据是独立同分布的，或者近似独立同分布的。一般有以下方法：
-
从数据源头采集更多数据
-
复制原有数据并加上随机噪声
-
重采样
-
数据增强（Data augmentation）：通过一定规则扩充数据。如在物体分类问题里，物体在图像中的位置、姿态、尺度，整体图片明暗度等都不会影响分类结果，那么就可以通过图像数据的空间变换（旋转、平移、翻转、镜像）、尺度变换（缩放、裁剪）、颜色变换、改变分辨率、对比度、亮度等手段将数据库成倍扩充。
-
生成式对抗网络（GAN）：用GAN可以生成大量的样本数据。
3.降低模型复杂度
调小模型复杂度，使其适合自己训练集的数量级（缩小宽度和减小深度），即减少模型参数数量。例如：对于LR，减少目标函数的因子数；对于DT，减少树的深度、剪枝等；对于DNN，减少层数和每层权向量长度。
4.提前停止训练（Early stopping）
对模型进行训练的过程即是对模型的参数进行学习更新的过程，这个参数学习的过程往往会用到一些迭代方法，如梯度下降（Gradient descent）学习算法。Early stopping便是一种迭代次数截断的方法来防止过拟合的方法，即在模型对训练数据集迭代收敛之前停止迭代来防止过拟合。
Early stopping方法的具体做法是，在每一个Epoch结束时（一个Epoch集为对所有的训练数据的一轮遍历）计算validation data的accuracy，当accuracy不再提高时，就停止训练。这种做法很符合直观感受，因为accurary都不再提高了，在继续训练也是无益的，只会提高训练的时间。那么该做法的一个重点便是怎样才认为validation accurary不再提高了呢？并不是说validation accuracy一降下来便认为不再提高了，因为可能经过这个Epoch后，accuracy降低了，但是随后的Epoch又让accuracy又上去了，所以不能根据一两次的连续降低就判断不再提高。一般的做法是，在训练的过程中，记录到目前为止最好的validation accuracy，当连续10次Epoch（或者更多次）没达到最佳accuracy时，则可以认为accuracy不再提高了。此时便可以停止迭代了（Early Stopping）。这种策略也称为“No-improvement-in-n”，n即Epoch的次数，可以根据实际情况取，如10、20、30……。
5.Dropout
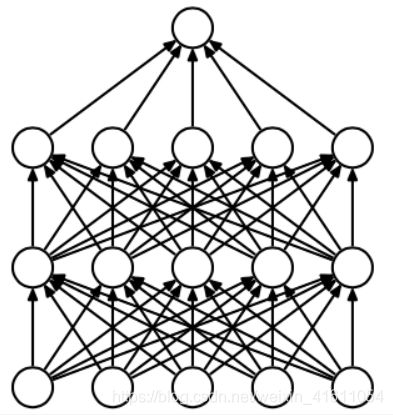
在神经网络中，有一种方法是通过修改神经网络本身结构来防止模型过拟合的，其名为Dropout。该方法是在对网络进行训练时用一种技巧（trick），对于如下所示的四层神经网络：
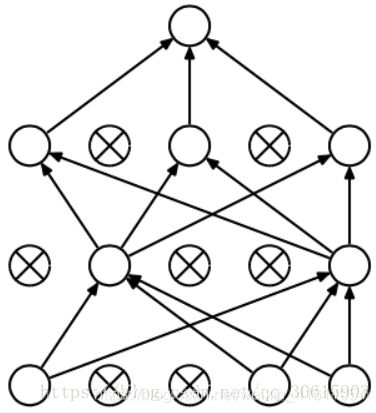
对于上图所示的网络，在训练开始时，随机的屏蔽一些（可以设定为一半，也可以为1/3，1/4等）隐藏层神经元，即使这些神经元的作用失效，同时保持输入层与输出层神经元的个数不变，就得到如下的神经网络：
然后按照BP学习算法对神经网络中的参数进行学习更新（被屏蔽的神经元不更新）。这样一次迭代更新便完成了。下一次迭代中，同样随机屏蔽一些神经元，与上次不一样，做随机选择。就这样一直进行随机屏蔽，直到训练结束。
6.正则化
正则化方法包括L0正则、L1正则和L2正则，而正则一般是在目标函数或代价函数之后加上对应的范数。
L0正则
目标函数后面加上在加入L0范数
，也就是权向量中非零参数的个数。它的特点是可以实现参数的稀疏性，使尽可能多的参数值为0，这与稀疏编码的思想吻合。但它的缺点是在优化时是NP难问题，很难优化。因此实际任务中更常用L1范数。
L1正则
L1正则是基于L1范数，在目标函数后面加上参数的L1范数和项，即全部权重
的绝对值的和，再乘以
，即：
其中
代表原始的代价函数，
是样本的个数，
就是正则项系数，权衡正则项与项的比重。后面那一项即为L1正则项。在计算梯度时，的梯度变为：
其中，
是符号函数，那么便使用下式对参数进行更新：
比原始的更新规则多出了
这一项。对于有些模型，如线性回归中（L1正则线性回归即为Lasso回归），常数项
的更新方程不包括正则项，即：
其中，
。从上式可以看出，当为正时，更新后会变小；当为负时，更新后会变大；因此L1正则项是为了使得那些原先处于零（即
）附近的参数往零移动，使得部分参数为零，从而降低模型的复杂度（模型的复杂度由参数决定），从而防止过拟合，提高模型的泛化能力。
其中，L1正则中有个问题，便是L1范数在0处不可导，即
在0处不可导，因此在为0时，使用原来的未经正则化的更新方程来对进行更新，即令
，这样即：
L1范数是L0范数的最优凸近似，比L0范数容易优化，而且也可以很好地实现参数稀疏性，常别称作“稀疏规则算子”（Lasso regularization），因此相对L0正则化更常用。同时L1和L0因为具有使参数稀疏的特点，常用于特征选择。
L2正则（权重衰减）
L2范数可以使得W的每个元素都很小，都接近于0，但与L1范数不同，它不会让它等于0，而是接近于0。L2正则是基于L2范数，即在目标函数后面加上参数的L2范数和项，即参数的平方和与参数的积项，即：
其中代表原始的代价函数，是样本的个数，与L1正则化项前面的参数不同的是，L2项的参数乘了1/2，是为了便于计算以及公式的美感性，因为平方项求导有个2，就是正则项系数，权衡正则项与项的比重。后面那一项即为L2正则项。
L2正则化中则使用下式对模型参数进行更新：
对于有些模型，如线性回归中（L2正则线性回归即为Ridge回归，岭回归），常数项的更新方程不包括正则项，即：
其中，，经变化后前面系数为
，由于
、、都是正的。所以小于1，它的效果是减小，这也就是权重衰减（weight decay）的由来。
从上式可以看出，L2正则项起到使得参数变小加剧的效果，但是为什么可以防止过拟合呢？一个通俗的理解便是：更小的参数值意味着模型的复杂度更低，对训练数据的拟合刚刚好（奥卡姆剃刀），而在实际应用中，也验证了这一点，L2正则化的效果往往好于未经正则化的效果。
在这里需要提到的是，在对模型参数进行更新学习的时候，有两种更新方式，mini-batch （部分增量更新）与 full-batch（全增量更新），即在每一次更新学习的过程中（一次迭代，即一次epoch），在mini-batch中进行分批处理，先使用一部分样本进行更新，然后再使用一部分样本进行更新。直到所有样本都使用了，这次epoch的损失函数值则为所有mini batch的平均损失值。设每次mini batch中样本个数为
，那么参数的更新方程中的L1、L2正则项分别要改成：
而full-batch即每一次epoch中，使用全部的训练样本进行更新，那么每次的损失函数值即为全部样本的误差之和。更新方程不变。
总结
正则项是为了降低模型的复杂度，从而避免模型区过分拟合训练数据，包括噪声与异常点（outliers）。从另一个角度上来讲，正则化即是假设模型参数服从先验概率，即为模型参数添加先验，只是不同的正则化方式的先验分布是不一样的。这样就规定了参数的分布，使得模型的复杂度降低（试想一下，限定条件多了，是不是模型的复杂度降低了呢），这样模型对于噪声与异常点的抗干扰性的能力增强，从而提高模型的泛化能力。还有个解释便是，从贝叶斯学派来看：加了先验，在数据少的时候，先验知识可以防止过拟合；从频率学派来看：正则项限定了参数的取值，从而提高了模型的稳定性，而稳定性强的模型不会过拟合，即控制模型空间。
由上图，过拟合从直观上理解便是，在对训练数据进行拟合时，需要照顾到每个点，从而使得拟合函数波动性非常大，即方差大。在某些小区间里，函数值的变化性很剧烈，意味着函数在某些小区间里的导数值的绝对值非常大，由于自变量的值在给定的训练数据集中一定的，因此只有系数足够大，才能保证导数的绝对值足够大。而L2正则化是通过约束參数的范数使其不要太大，所以能够在一定程度上降低过拟合情况。
L2与L1的区别在于，L1正则是拉普拉斯先验，而L2正则则是高斯先验。如下图：
可以看出，服从拉普拉斯分布的L1正则项更倾向于产生稀疏参数，而服从高斯分布的L2正则项在0处相对比较平滑，在参数绝对值较大处抑制效果更好，使整体数据的分布更接近0。它们都是服从均值为0，协方差为
。当
时，即没有先验，没有正则项，则相当于先验分布具有无穷大的协方差，那么这个先验约束则会非常弱，模型为了拟合所有的训练集数据， 参数可以变得任意大从而使得模型不稳定，即方差大而偏差小。越大，标明先验分布协方差越小，偏差越大，模型越稳定。即，加入正则项是在偏差bias与方差variance之间做平衡tradeoff。有些任务中会同时使用L1和L2正则项，用各自的两个正则化参数去权衡“部分稀疏”与“整体接近0”这一对trade-off问题。下图即为L2与L1正则的区别：
上图中的模型是线性回归，有两个特征，要优化的参数分别是w1和w2，左图的正则化是L2，右图是L1。蓝色线就是优化过程中遇到的等高线，一圈代表一个目标函数值，圆心就是样本观测值（假设一个样本），半径就是误差值，受限条件就是红色边界（就是正则化那部分），二者相交处，才是最优参数。可见右边的最优参数只可能在坐标轴上，所以就会出现0权重参数，使得模型稀疏。
7.多模型投票
类似集成学习方法的思想，不同模型可能会从不同角度去拟合，互相之间取长补短，即使单独使用某个模型已出现过拟合，但综合起来却有可能减低过拟合程度，起到正则作用，提高了泛化效果。特别是使用多个非常简单的模型，更不容易产生过拟合。
8.（针对DNN）batch normalization
即BN，既能够提高泛化能力，又大大提高训练速度，现在被广泛应用在DNN中的激活层之前。BN的提出最初是针对DNN在训练过程中会出现数据内部的协方差偏移现象，导致输出数据分布发生额外的改变，并随着层数的增加偏移加剧，使得模型不得不根据输出分布的改变重新学习，这又导致训练速度减慢。公式如下：
具体过程：首先对某层的输入样本做白化处理，等价于零均值化处理(均值为0，方差为1)，使输入样本之间互不相关，且每层的输入服从相同分布，克服了内部协方差偏移的影响。采用分批处理数据的方式，减少了计算量。
主要优势：减小了梯度对参数大小和初始值的依赖，将参数值（特征）缩放在[0,1]区间（若针对Relu还限制了输出的范围），这样反向传播时梯度控制在1左右，使网络即使在较高学习率下也不易发生梯度爆炸或弥散（也预防了在使用sigmoid作为激活函数时训练容易陷入梯度极小饱和或极大的极端情况）。
9.调整参数和超参数
- 超参数（在开始学习过程之前设置值的参数，而不是通过训练得到的参数数据）包括：
- 神经网络：学习率、学习衰减率、隐藏层数、隐藏层的单元数、Adam优化算法中的β1和β2参数、batch_size数值等
- 其他算法：随机森林的树数量，k-means中的cluster数，正则化参数λ等