(EWC)Overcoming Catastrophic Forgetting in Neural Network
论文链接:Overcoming Catastrophic Forgetting in Neural Network
1.论文基础思路
文章开发了一种类似于人工神经网络突触整合的算法,我们称之为弹性权重整合(简称EWC)。该算法会根据某些权重对以前看到的任务的重要性来减慢对它们的学习速度。
EWC这个算法降低重要权重的学习率,重要权重的决定权是以前任务中的重要性。
作者尝试在人工神经网络中识别对旧任务而言较为重要的神经元,并降低其权重在之后的任务训练中的改变程度,识别出较为重要的神经元后,需要更进一步的给出各个神经元对于旧任务而言的重要性排序
论文通过给权重添加正则,从而控制权重优化方向,从而达到持续学习效果的方法。其方法简单来讲分为以下三个步骤:
1. 选择出对于旧任务(old task)比较重要的权重
2. 对权重的重要程度进行排序
3. 在优化的时候,越重要的权重改变越小,保证其在小范围内改变,不会对旧任务产生较大的影响
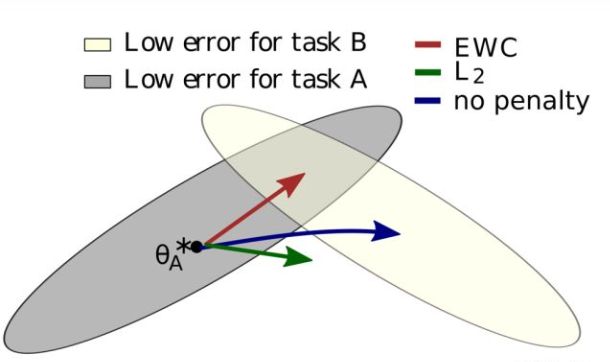
论文示意图,灰色区域是先前任务A的参数空间(旧任务的低误差区域),米黄色区域是当前任务B的参数空间(新任务的低误差区域);
如果我们什么都不做,用旧任务(Task A)的权重初始化网络,用新任务(Task B)的数据进行训练的话,在学习完Task A之后紧接着学习Task B,相当于Fine-tune(图中蓝色箭头),优化的方向如蓝色箭头所示,离开了灰色区域,最优参数将从原先A直接移向B中心,代表着其网络失去了在旧任务上的性能;
如果加上L2正则化就如绿色箭头所示;
如果用论文中的正则化方法EWC(红色箭头),参数将会移向Task A和Task B的公共区域(在学习任务B之后不至于完全忘记A)便代表其在旧任务与新任务上都有良好的性能。
具体方法为:将模型的后验概率拟合为一个高斯分布,其中均值为旧任务的权重,方差为 Fisher 信息矩阵(Fisher Information Matrix)的对角元素的倒数。方差就代表了每个权重的重要程度。
2.基础知识
2.1贝叶斯法则
P ( A ∣ B ) P(A∣B) P(A∣B)= P ( A ∩ B ) P ( B ) \frac{P(A∩B)}{P(B)} P(B)P(A∩B)
P ( B ∣ A ) P(B∣A) P(B∣A)= P ( A ∩ B ) P ( A ) \frac{P(A \cap B)}{P(A)} P(A)P(A∩B)
即
P ( A ∣ B ) P ( B ) P(A∣B)P(B) P(A∣B)P(B)= P ( B ∣ A ) P ( A ) P(B∣A)P(A) P(B∣A)P(A)
所以可以得到
P ( B ∣ A ) P (B∣A) P(B∣A) == P ( A ∣ B ) P(A|B) P(A∣B) P ( B ) P ( A ) \frac{P( B)}{P(A)} P(A)P(B)
3.Elastic Weight Consolidation
3.1 参数定义
θ \theta θ:网络的参数
θ A ∗ \theta^*_A θA∗ :对于任务A,网络训练得到的最优参数
D D D:全体数据集
D A D_A DA:任务 A 的数据集
D B D_B DB :任务 B 的数据集
F F F:Fisher 信息矩阵
H H H:Hessian 矩阵
3.2 EWC 方法推导
给定数据集D,我们的目的是寻找一个最优的参数 θ \theta θ,即目标为
log P ( θ ∣ D ) \log P(\theta|D) logP(θ∣D) ----------------------------------------------------------------(1.0)
此类目标和我们常用的极大似然估计不一致,其实这么理解也是可行的,对1.0进行变化,则有
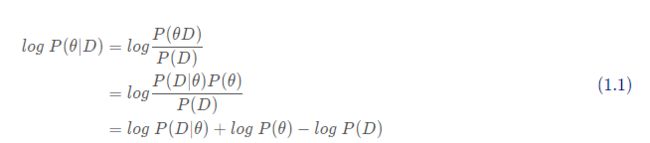
假设D由task A与task B的数据集 D A D_A DA 、 D B D_B DB 组成,则有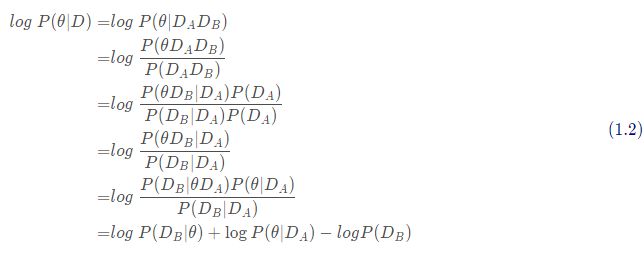
由于 D A D_A DA 、 D B D_B DB 相互独立,则有
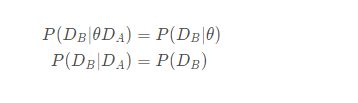
式1.2是全文的核心
两边取对数,得到论文中的优化目标:
log P ( θ ∣ D A , D B ) \log P(\theta∣D_A ,D_B) logP(θ∣DA,DB)= log P ( D B ∣ θ ) \log P(D_B∣\theta) logP(DB∣θ)+ log P ( θ ∣ D A ) \log P(\theta|D_A) logP(θ∣DA)− log P ( D B ) \log P(D_B ) logP(DB)
在给定整个数据集,我们需要得到一个 θ \theta θ使得概率最大,那么也就是分别优化上式的右边三项。
第一项 log P ( D B ∣ θ ) \log P(D_B∣\theta) logP(DB∣θ)是任务 B B B的似然,很明显可以理解为任务B的损失函数,将其命名为 L B ( θ ) L_B(\theta) LB(θ),第三项 log P ( D B ) \log P(D_B ) logP(DB)对于 θ \theta θ来讲是一个常数, log P ( θ ∣ D A ) \log P(\theta|D_A) logP(θ∣DA)是任务 A A A上的后验,我们要最大化 log P ( θ ∣ D A , D B ) \log P(\theta∣D_A ,D_B) logP(θ∣DA,DB),那么网络的优化目标便是:
m a x max max log P ( θ ∣ D A , D B ) \log P(\theta∣D_A ,D_B) logP(θ∣DA,DB)= m a x max max ( log P ( D B ∣ θ ) \log P(D_B∣\theta) logP(DB∣θ)+ log P ( θ ∣ D A ) \log P(\theta|D_A) logP(θ∣DA))
即
m a x max max log P ( θ ∣ D ) \log P(θ∣D) logP(θ∣D)= m a x max max ( − L B ( θ ) + l o g P ( θ ∣ D A ) (−L_B(θ)+logP(θ∣D_A ) (−LB(θ)+logP(θ∣DA))
右边提取负号,最大化一个负数 m a x max max − ( L B ( θ ) − l o g P ( θ ∣ D A ) -(L_B(θ)-logP(θ∣D_A ) −(LB(θ)−logP(θ∣DA))
,相当于最小化负号后面的正数,即
m i n min min ( L B ( θ ) − l o g P ( θ ∣ D A ) ) (L_B(θ)-log P(θ∣D_A)) (LB(θ)−logP(θ∣DA))
最小化Task B上的损失函数,这很容易求,但后验概率 l o g P ( θ ∣ D A ) log P(\theta|D_A) logP(θ∣DA)很难求,我们只有上一次Task A训练完的模型参数 θ A \theta_A θA,,现在工作重点将转换为如何优化后验概率 l o g P ( θ ∣ D A ) log P(\theta|D_A) logP(θ∣DA) ,作者采用了拉普拉斯近似的方法进行量化。
3.3 拉普拉斯近似
由于后验概率并不容易进行衡量,所以我们将其先验 log P ( D A ∣ θ ) \log P(D_A|\theta) logP(DA∣θ) 拟合为一个高斯分布
3.3.1 高斯分布拟合
令先验 log P ( D A ∣ θ ) \log P(D_A|\theta) logP(DA∣θ) 服从高斯分布
P ( D A ∣ θ ) P(D_A|\theta) P(DA∣θ) ∼ N ( μ , σ ) N(μ,σ) N(μ,σ)
那么由高斯分布的公式可以得到:
P ( D A ∣ θ ) P(D_A|\theta) P(DA∣θ) = 1 2 π σ e − ( θ − μ ) 2 2 σ 2 \frac{1}{\sqrt{2 \pi}\sigma} e^{-\frac{(\theta-\mu)^2}{2\sigma^2}} 2πσ1e−2σ2(θ−μ)2
取对数 log P ( D A ∣ θ ) \log P(D_A|\theta) logP(DA∣θ) = log 1 2 π σ + log e − ( θ − μ ) 2 2 σ 2 \log \frac{1}{\sqrt{2 \pi}\sigma} +\log e^{-\frac{(\theta-\mu)^2}{2\sigma^2}} log2πσ1+loge−2σ2(θ−μ)2
那么,可以得到
log P ( D A ∣ θ ) \log P(D_A|\theta) logP(DA∣θ)= log 1 2 π σ − ( θ − μ ) 2 2 σ 2 \log \frac{1}{\sqrt{2 \pi}\sigma} -\frac{(\theta-\mu)^2}{2\sigma^2} log2πσ1−2σ2(θ−μ)2
令 f ( θ ) f(\theta) f(θ)= log P ( D A ∣ θ ) \log P(D_A|\theta) logP(DA∣θ)
在 θ \theta θ = θ A ∗ \theta_A^* θA∗ 处进行泰勒展开,
f ( θ ) f(\theta) f(θ)= f ( θ A ∗ ) + f ′ ( θ A ∗ ) ( θ − θ A ∗ ) + f ′ ′ ( θ A ∗ ) ( θ − θ A ∗ ) 2 2 + o ( θ A ∗ ) f(\theta_A^*)+f'(\theta_A^*)(\theta-\theta_A^*)+f''(\theta_A^*)\frac{(\theta-\theta_A^*)^2}{2}+o(\theta_A^*) f(θA∗)+f′(θA∗)(θ−θA∗)+f′′(θA∗)2(θ−θA∗)2+o(θA∗)
θ A ∗ \theta_A^* θA∗是最优解,可以得到 f ′ ( θ A ∗ ) f'(θ_A^∗) f′(θA∗)=0
所以
f ( θ ) f(\theta) f(θ)= f ( θ A ∗ ) + f ′ ′ ( θ A ∗ ) ( θ − θ A ∗ ) 2 2 + o ( θ A ∗ ) f(\theta_A^*)+f''(\theta_A^*)\frac{(\theta-\theta_A^*)^2}{2}+o(\theta_A^*) f(θA∗)+f′′(θA∗)2(θ−θA∗)2+o(θA∗)
那么可以得到
log 1 2 π σ − ( θ − μ ) 2 2 σ 2 \log \frac{1}{\sqrt{2 \pi}\sigma} -\frac{(\theta-\mu)^2}{2\sigma^2} log2πσ1−2σ2(θ−μ)2≈ f ( θ A ∗ ) + f ′ ′ ( θ A ∗ ) ( θ − θ A ∗ ) 2 2 f(\theta_A^*)+f''(\theta_A^*)\frac{(\theta-\theta_A^*)^2}{2} f(θA∗)+f′′(θA∗)2(θ−θA∗)2
其中 log 1 2 π σ \log \frac{1}{\sqrt{2 \pi}\sigma} log2πσ1与 f ( θ A ∗ ) f(\theta_A^*) f(θA∗)都是常数,可以得到
因此,可以得到
μ \mu μ = θ A ∗ \theta_A^* θA∗
σ 2 = − 1 f ′ ′ ( θ A ∗ ) \sigma^2=-\frac{1}{f''(\theta_A^*)} σ2=−f′′(θA∗)1
所以,可以得到
P ( D A ∣ θ ) ∼ N ( θ A ∗ , − 1 f ′ ′ ( θ A ∗ ) ) P(D_A|\theta) \sim N(\theta_A^*, -\frac{1}{f''(\theta_A^*)}) P(DA∣θ)∼N(θA∗,−f′′(θA∗)1)
根据贝叶斯准则,
P ( θ ∣ D A ) P(\theta|D_A) P(θ∣DA)= P ( D A ∣ θ ) P ( θ ) P ( D A ) \frac{P(D_A|\theta)P(\theta)}{P(D_A)} P(DA)P(DA∣θ)P(θ)
其中, P ( θ ) P(\theta) P(θ)符合均匀分布, P ( D A ) P(D_A) P(DA)为常数,所以后验概率 P ( θ ∣ D A ) P(\theta|D_A) P(θ∣DA)也同先验概率服从同样的高斯分布
P ( θ ∣ D A ) ∼ N ( θ A ∗ , − 1 f ′ ′ ( θ A ∗ ) ) P(\theta|D_A) \sim N(\theta_A^*, -\frac{1}{f''(\theta_A^*)}) P(θ∣DA)∼N(θA∗,−f′′(θA∗)1)
此时,优化函数
m i n min min ( L B ( θ ) − l o g P ( θ ∣ D A ) ) (L_B(θ)-log P(θ∣D_A)) (LB(θ)−logP(θ∣DA))
可以变换为
m i n min min ( L B ( θ ) − f ′ ′ ( θ A ∗ ) ( θ − θ A ∗ ) 2 2 ) (L_B(θ)-f''(\theta_A^*)\frac{(\theta-\theta_A^*)^2}{2}) (LB(θ)−f′′(θA∗)2(θ−θA∗)2)
将权重展开来说,即为
m i n min min ( L B ( θ ) − ∑ i f i ′ ′ ( θ A ∗ ) ( θ i − θ A , i ∗ ) 2 2 ) (L_B(θ)-∑_if''_i(\theta_A^*)\frac{(\theta_i-\theta_{A,i}^*)^2}{2}) (LB(θ)−∑ifi′′(θA∗)2(θi−θA,i∗)2)
其中 f i ′ ′ ( θ A ∗ ) f''_i(\theta_A^*) fi′′(θA∗)该如何求解?
f i ′ ′ ( θ A ∗ ) f''_i(\theta_A^*) fi′′(θA∗)相当于之前Task A模型参数的Hessian矩阵 H H H ,直接求这个n*n的海森的话计算量太大了,作者提出用Fisher信息对角矩阵 F F F 替代,它与海森矩阵有如下关系:
F θ X F_\theta^X FθX= − E X [ H θ ] -E_X[H_\theta] −EX[Hθ]
如果再假设Fisher矩阵是对角的,则可以得到EWC算法:
m i n θ ( L B ( θ ) + λ 2 ∑ i F i ( θ i − θ A , i ∗ ) 2 ) \mathop{min}\limits_{\theta}(L_B(\theta)+\frac{\lambda}{2}\sum_i F_i(\theta_i-\theta_{A,i}^*)^2) θmin(LB(θ)+2λ∑iFi(θi−θA,i∗)2)
引入超参 λ \lambda λ 衡量两项的重要程度
因为 Fisher 信息矩阵是海森矩阵的期望取负,所以这里从减号变成了加号
上式即为论文中的公式(3)
Fisher信息矩阵本质上是海森矩阵的负期望,求 H H H需要求二阶导,而 F F F只需要求一阶导,所以速度更快, F F F有如下性质:
1. 相当于损失函数极小值附近的二阶导数
2. 能够单独计算一阶导数(对于大模型而言方便计算)
3. 半正定矩阵
总结一句话:EWC的核心思想就是利用模型在Task A上训练的参数 θ A ∗ \theta_A^* θA∗ 来估计后验 P ( θ ∣ D A ) P(\theta|D_A) P(θ∣DA),其中估计的方法采用的是拉普拉斯近似,最后用Fisher对角矩阵代替Hessian计算以提高效率。
当移动到第三个任务(任务C)时,EWC将尝试保持网络参数接近任务a和B的学习参数。这可以通过两个单独的惩罚来实现,或者通过注意两个二次惩罚的总和本身就是一个二次惩罚来实现。
4.讨论
文章提出了一种新的算法,弹性权重整合(elastic weight consolidation),解决了神经网络持续学习的重要问题。EWC允许在新的学习过程中保护以前任务的知识,从而避免灾难性地忘记旧的能力。它通过选择性地降低体重的可塑性来实现,因此与突触巩固的神经生物学模型相似。
EWC算法可以基于贝叶斯学习方法。从形式上讲,当有新任务需要学习时,网络参数由先验值进行调整,先验值是前一任务中给定参数的后验分布。这使得受先前任务约束较差的参数的学习速度更快,而对那些至关重要的参数的学习速度较慢。
4.2 Fisher Information Matrix
4.2.1 Fisher Information Matrix 的含义
E ( x ) = ∫ x f ( x ) d x E(x)=∫xf(x)dx E(x)=∫xf(x)dx
∇ l o g x = ∇ x x ∇log x=\frac{∇x}{x} ∇logx=x∇x
Fisher information 是概率分布梯度的协方差。为了更好的说明Fisher Information matrix 的含义,这里定义一个得分函数 S S S
S ( θ ) = ∇ log p ( x ∣ θ ) S(\theta)=\nabla \log p(x|\theta) S(θ)=∇logp(x∣θ)
则
E p ( X ∣ θ ) \mathop{E}\limits_{p(X|\theta)} p(X∣θ)E[ S ( θ ) S(\theta) S(θ)]= E p ( X ∣ θ ) \mathop{E}\limits_{p(X|\theta)} p(X∣θ)E [ ∇ l o g p ( x ∣ θ ) ] [∇logp(x∣θ)] [∇logp(x∣θ)]
= ∫ ∇ l o g p ( x ∣ θ ) ⋅ p ( x ∣ θ ) d θ ∫∇logp(x∣θ)⋅p(x∣θ)dθ ∫∇logp(x∣θ)⋅p(x∣θ)dθ
= ∫ ∇ p ( x ∣ θ ) p ( x ∣ θ ) ⋅ p ( x ∣ θ ) d θ ∫\frac{∇p(x∣θ)}{p(x∣θ)}⋅p(x∣θ)dθ ∫p(x∣θ)∇p(x∣θ)⋅p(x∣θ)dθ
= ∫ ∇ p ( x ∣ θ ) d θ ∫∇p(x∣θ)dθ ∫∇p(x∣θ)dθ
= ∇ ∫ p ( x ∣ θ ) d θ ∇∫p(x∣θ)dθ ∇∫p(x∣θ)dθ
= ∇ 1 ∇1 ∇1=0那么 Fisher Information matrix F F F为
F = E p ( X ∣ θ ) F = \mathop{E}\limits_{p(X|\theta)} F=p(X∣θ)E[( S ( θ ) − 0 S(\theta)-0 S(θ)−0)( S ( θ ) − 0 ) T S(\theta)-0)^T S(θ)−0)T]对于每一个batch的数据 X = { x 1 , x 2 , ⋯ , x n } X = \{x_1,x_2,\cdots ,x_n\} X={x1,x2,⋯,xn},则其定义为
F = 1 N ∑ i N ∇ l o g p ( x i ∣ θ ) ∇ l o g p ( x i ∣ θ ) T F=\frac{1}{N}∑_i^N∇logp(x_i ∣θ)∇logp(x_i∣θ)^T F=N1∑iN∇logp(xi∣θ)∇logp(xi∣θ)T
4.2.2 Fisher 信息矩阵与 Hessian 矩阵
参考1:高斯分布的积分期望E(X)方差V(X)的理论推导
参考2:《Overcoming Catastrophic Forgetting in Neural Network》增量学习论文解读
参考3:深度学习论文笔记(增量学习)——Overcoming catastrophic forgetting in neural networks
参考4:Elastic Weight Consolidation
参考5:(Fisher矩阵)持续学习:(Elastic Weight Consolidation, EWC)Overcoming Catastrophic Forgetting in Neural Network