五子棋入门级AI的设计与实现
实现代码https://download.csdn.net/download/u014541881/86894096
为什么选择五子棋?
五子棋是博弈游戏当中较简单的一种玩法,规则、赢法都很简单,其 AI 的设计也相对简单,而且目前市面上已经有了很多的五子棋游戏及开源代码,因此用五子棋来入门,是一个非常好的选择。这里和大家分享一些我的学习经历,主要记录五子棋 AI 的设计和实现过程,不介绍界面的实现。
FIRST 【博弈树 game tree】
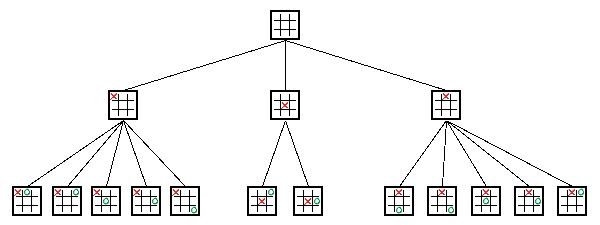
“博弈树是指由于动态博弈参与者的行动有先后次序,因此可以依次将参与者的行动展开成一个树状图形”,这是 wikipedia 对于博弈树的解释,顾名思义,博弈树就对博弈双方以相同的次数轮流进行决策行为的图形描述。对于任何一种博弈竞赛,我们都可以将其构建成一颗博弈树,其节点对应某一种棋局,其分支表示进行一步决策,博弈树的根表示开始位置,叶子节点表示博弈到此结束。
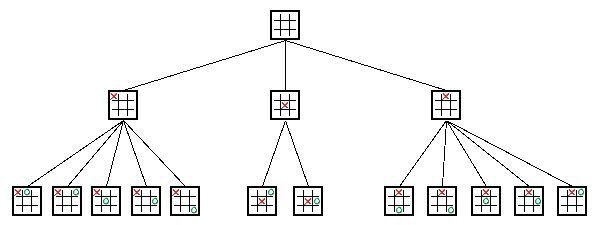
Second 【极大极小值搜索算法
the min-max algorithm
】
有了博弈树的概念后,我们需要做的是对这棵巨大的博弈树进行搜索,由于博弈树的每一个分支都是一步决策,因此我们需要对其进行深度优先搜索,这里我们用的是极大极小值搜索算法。其中极大极小值定理是 von Neumann 和 Borel 在上世纪 20 年代提出的,是搜索算法的数学基础,定理具体内容不做介绍。极大极小值搜索算法是一种在失败的可能性中找出最小值的方法,通俗的说就是最小化对手的最大利益,这种算法通常用递归实现
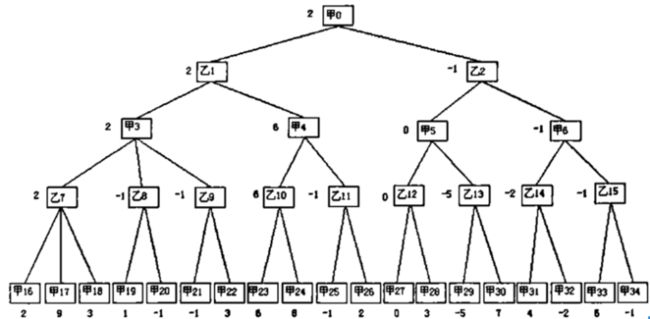
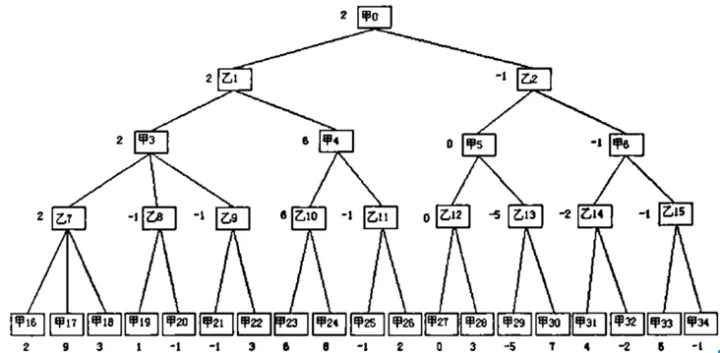
如上图所示,假设甲为 AI,乙为玩家
我们需要在双方走每一步棋后对棋局进行评估,得到一个分数,规定这个分数越大,对玩家越有利,反之对 AI 更有利
因此 :
AI 走的层我们成为MIN层,在这一层 AI 要选择分值最低的点走以保障自己的利益最大化;
玩家走的层我们成为MAX层,在这一次玩家要选择分值最高的点走以保障自己的利益最大化;
通俗的说,AI 在玩家落子后,遍历所有可走的位置,模拟玩家落子,并对每一种走法进行评估,选择对自己最有利的一步棋。那么,我们就需要一个能对当下局势做出评估的方法,下面说说至关重要的评估函数。
Third【评估函数 evaluate function】
评估函数(也称评价函数)是博弈类游戏中 AI 的重要一部分,它决定了 AI 的决策步骤 ,主要任务是评估节点的重要程度,通俗的讲,评估函数为 AI 评估目前的对局形式,也为 AI 模拟每一步决策后的对局形式,并决策出于 AI 最有利、于对方最不利的一步。
评估函数的设计中最重要的一步,也是非常复杂的一个环节,是一个建立数学模型的过程,通常为:
G(s) = a1 * f1(s) + a2 * f2(s) + a3 * f3(s) + . . . + an * f(n)
其中 s 为当前的局面,fi(s) 为某个评估因素的得分, ai 为某个评估因素的权重比
然后,回到我们的五子棋,我们该如何设计评估函数呢?这就需要一些五子棋的棋局知识了,五子棋对弈的过程中,一定会出现以下这些情况:
五子 : 这种情况表示已经有一方赢得了本次对弈,出现这种情况时,我们给当前局势的评分为无穷大(infinity)
双四 : 一方出现了两个四子相连,且均为被堵死,这种情况被认为极有可能获胜,设评分为 10000
单四 : 一方出现了一个四子相连,且未被堵死,这种情况被认为有较大可能获胜,设评分为 5000
双三 : 一方出现了两个三子相连,且均为被堵死,这种情况被认为有较大优势,设评分为 2000
单三 : 一方出现了一个三子相连,且未被堵死,这种情况被认为有优势,设评分为 1000
双二 : 一方出现了两个二子相连,且均未被堵死,这种情况我们设评分为 500
单二 : 一方出现了一个二子相连,且未被堵死,设评分为 200
一子 : 只有一子,设评分为 10
上面这些就是我们刚才说的 评估因素 的 权重比 (ai)。但是仅有这些权重比是不够的,我们还需要上面公式中的 fi(),也就是一个能根据当前局面给出得分的方法,下面就说说如何设计这个 fi():
我们需要引入一个新的概念,赢法数组。大家都知道,博弈类游戏的结束一定是因为某一方触发了获胜条件或是双方在规定时间、范围内没有分出胜负,即打成平手;因此我们需要记录所有的获胜条件,在对弈者每一步决策后判断其是否触发了获胜条件,而存储获胜条件的结构我们就称之为:赢法数组。说到这里可能会有人问:在五子棋中判断是否获胜只要在棋子的周围统计同类棋子的个数不就行了吗? 没错,这确实是一种简便的判断获胜的方法,但是我们的赢法数组还有另外一个重要的功能,协助 fi() 得出分数。
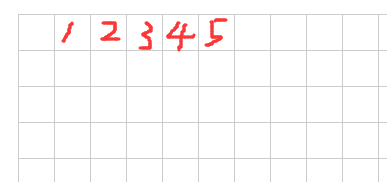
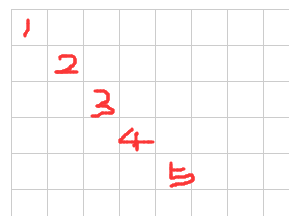
那么赢法数组是如何协助得出分数的呢? 首先,我们需要把五子棋的所有赢法存入该数组,如图所示,不同的位置代表了不同的赢法,在 15 x 15 的棋盘中,一共有 572 种赢法。



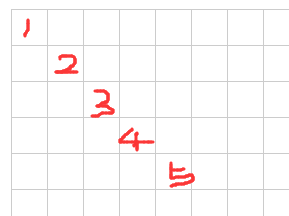
有了所有的赢法之后,我们就可以给出得分了:对于每一种种赢法,我们需要统计该赢法的位置上己方棋子和对方棋子的数目,同样可以存储在一个数组中,然后在每一次需要对当前局势评估时,如果某种赢法上只有己方棋子或只有对方棋子,根据棋子的的数目就是该点的权重,也就是 fi() 得出的值,在和预设的评分 ai 相乘,将总分相加,就得出了当前局势下某一方的评估分数。
通过这样的方法,我们可以得到两个数字,分别是 玩家 和 AI 的当前优势值,我们将这两个数字做差,返回 MAX - MIN 的值,这就是该种走法的分数,也就是博弈树种叶子节点的值,值越大对玩家更有利,值越小对 AI 更有利。
【Then】
到这里,我们的五子棋 AI 已经设计完成了,AI 会模拟玩家落子,然后对每一种走法进行评估,选出最优解。这样的 AI 已经可以和人类玩家进行对战了。
但是它还有一个很大的缺点——速度很慢,想想看,我们最开始提到的那棵博弈树,它是非常非常庞大的,我们几乎不可能对整棵树进行搜索,这样的代价实在太大了,现实中我们一般会设置搜索层数,也就是 AI 会往后看几步棋。 我们来做一个简单的计算,假设 AI 平均一步需要考虑 50 种可能的走法,当看到第四步的时候,需要搜索的节点数为 50^4 = 625w 个,这么多的节点,计算机需要比较长的时间去‘思考’,我们不愿意长时间去等待 AI 落子,那么就需要在搜索上动些脑筋了。
Fourth【Alpha-Beta剪枝算法
alpha-beta pruning algorithm
】
上面我们说到,人类玩家是不愿意长时间等待计算机‘思考’的 ,要减少搜索树的时间,常用的方法是剪枝,剪去没有意义的分支来降低搜索次数,提高搜索速度,这里我们要用到的是 Alpha-Beta剪枝算法。
Alpha-Beta剪枝算法是在极大极小值搜索算法上的一种改进,它是一种对抗性搜索算法,当算法评估出某策略的后续走法比之前的策略还差时,就会停止该策略的后续搜索,相当于剪去了不影响最终决定的分枝。
算法将会用到两个值:alpha 和 beta,分别代表人类玩家能够接受的最低分和 AI 能够接受的最高分,一旦出现beta <= alpha ,我们认为父节点不会选择这个节点,因为选择这个节点会为自己带来不利,因此该分枝的其他节点也就没有了搜索的必要。
下面我们通过一个例子来理解 Alpha-Beta剪枝算法,这个例子参考来源于一篇博客 ,如果没看懂我的描述,请移步
一看就懂的Alpha-Beta剪枝算法详解首先明确,alpha 为下界,beta 为上界,一旦下界大于等于上届,我们就可以剪枝,停止对当前分枝的搜索。
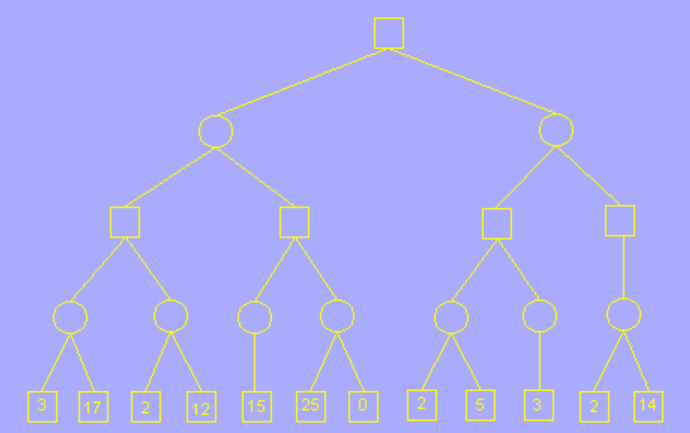
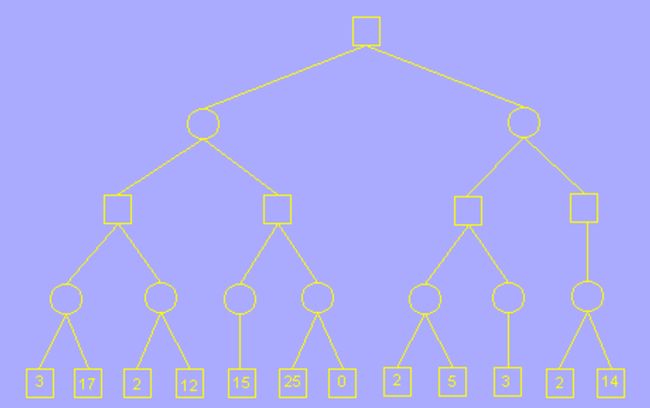
这是我们要搜索的完整的树,正方形代表 玩家, 圆形代表 AI
alpha 的初始值为负无穷大,beta 为正无穷大;这里我们只用根节点左子树的一部分举例,其余过程雷同
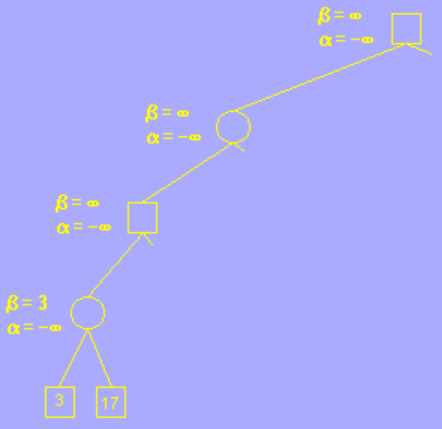
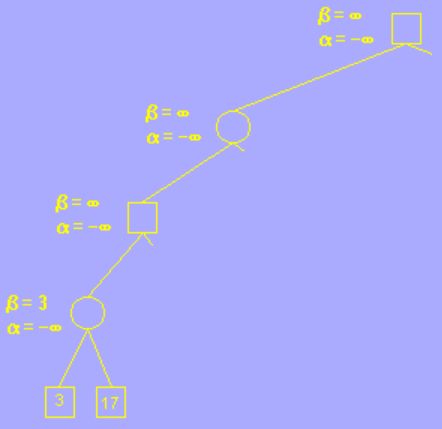
在未到叶子节点之前,每个节点的 alpha beta 值均继承自父节点,如图所示,第一个叶子节点的评估分为 3,也就是说AI 在这一步的决策中,玩家至少可以获得一个价值为 3 分的棋局,由于第四层为AI层(MIN层),AI 应尽量让玩家更少的获利,所以修改 beta 值为 3,意为这一步 AI 最多只接受玩家获利 3 分; 再搜索下一个叶子节点,值为 17,大于 3,因此 beta 值不变。
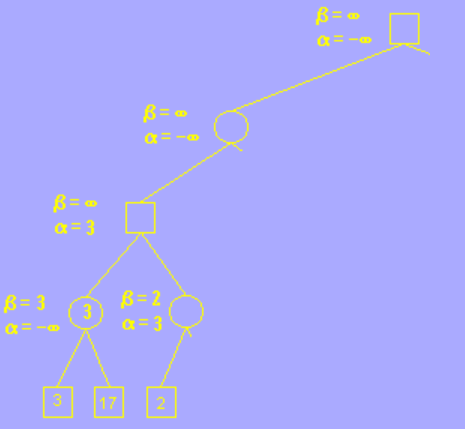
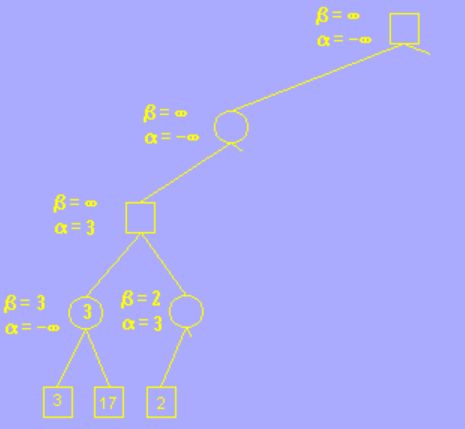
该分支的叶子节点搜索完后,向父节点返回,并确定第四层的分支为 3,意为在这一步 AI 会选择走价值为 3 分的这一步棋,以让玩家更少的获利,继续回到第三层,这一层为玩家层(MAX层),玩家应尽量选择分值较大的步骤走,以让自己获利更多,因此我们更新 alpha 的值为其子节点的 beta 值,意为在这一步的决策中,玩家最少接收自己获利 3 分;
随后搜索另一个分支,在这个分枝的叶子节点中,我们发现了一个节点的分枝为 2,小于 3,更新 beta 值为 2 后发现 beta <= alpha,符合剪枝条件,因此剪枝,不在搜索该分枝的其它叶子节点;
通俗的说就是,如果玩家在第三层选择右边的方案,那么 AI 就一定有一步棋可以只让玩家的获利只有 2 分,也就是比左边方案的 3 分少,因此 AI 可以认为玩家在第三层做决策时不会选择右边的方案,因为这样玩家自己的获利更小,所以这一方案其他的步骤就不用考虑了。 这就是剪枝操作。
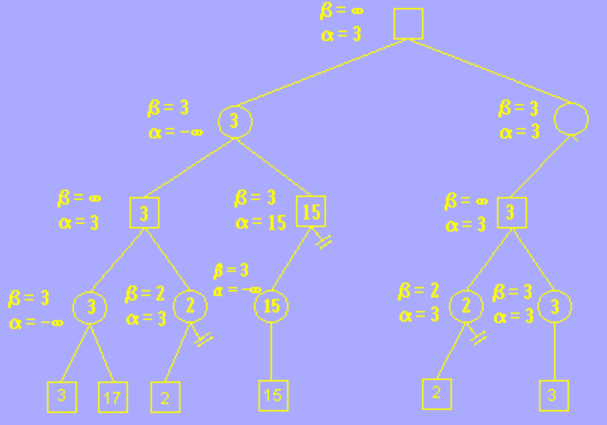
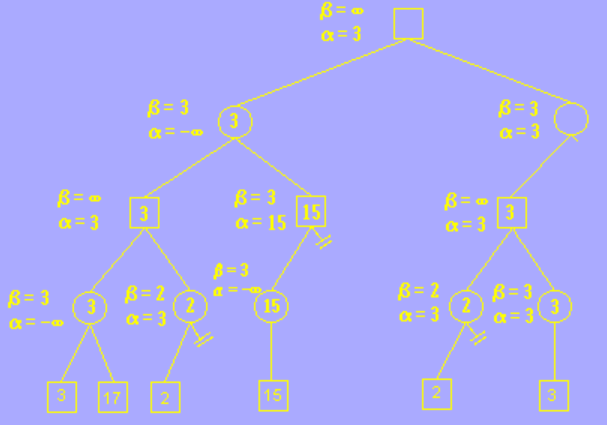
其他分枝的搜索与上述方法一样,我们这里展示最终剪枝完毕的结果。可以发现原本需要搜索 12 个几点,而剪枝完后我们的程序只需要搜索 6 个节点,当数量非常庞大时,剪枝操作会大大提升搜索算法的效率
【Finally】
上面简述的方法都是比较简单的、入门级的,如果需要提高 AI 的智能程度和思考速度,我们还有大量的工作需要做,比如 简化 AI 决策时的考虑范围、采用更高级的搜索算法、强化走法生成函数等等