Bezier曲线与B-Spline曲线
微分几何基础
微分集合是用微分的方法来研究曲线的局部性质,如曲线的弯曲程度等。
一条可以用参数表示的三维曲线是一个有界点集,可以写成一个带参数的、连续的、单值的数学函数:
{ x = x ( t ) y = y ( t ) z = z ( t ) 0 ⩽ t ⩽ 1 p = p ( t ) t ∈ [ 0 , 1 ] p ′ ( t ) = d p d t p ′ ′ ( t ) = d 2 p d t 2 \begin{aligned} &\begin{cases} x=x(t)\\ y=y(t)\\ z=z(t) \end{cases} 0\leqslant t\leqslant 1\\ &\quad p=p(t)\quad t\in[0,1]\\ &\quad p'(t)=\dfrac{{\rm d}p}{{\rm d}t}\\ &\quad p''(t)=\dfrac{{\rm d}^2p}{{\rm d}t^2} \end{aligned} ⎩⎪⎨⎪⎧x=x(t)y=y(t)z=z(t)0⩽t⩽1p=p(t)t∈[0,1]p′(t)=dtdpp′′(t)=dt2d2p
位置矢量
贝塞尔曲线
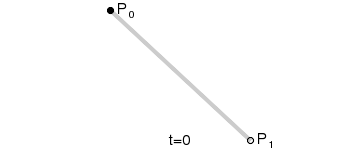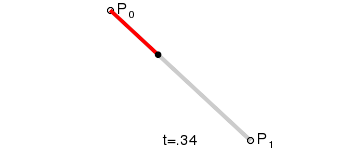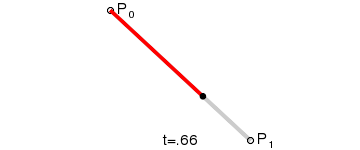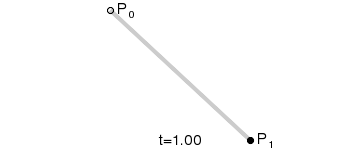
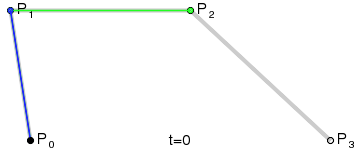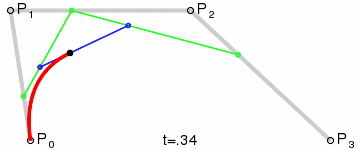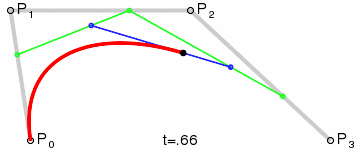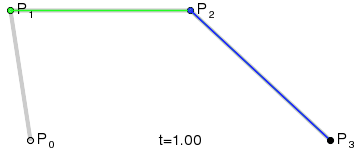
一阶贝塞尔曲线 P 0 1 P_0^1 P01由两个控制点 P 0 P_0 P0和 P 1 P_1 P1完全定义,相当于线性插值。随着 t t t从0到1变化,贝塞尔点从 P 0 P_0 P0移动到 P 1 P_1 P1.
P 0 1 = ( 1 − t ) P 0 + t P 1 , t ∈ [ 0 , 1 ] P_{0}^{1}=\left( 1-t\right) P_{0}+tP_{1}\quad,t\in[0,1] P01=(1−t)P0+tP1,t∈[0,1]

二阶贝塞尔曲线由一阶贝塞尔曲线递归定义。三个控制点 P 0 P_0 P0、 P 1 P_1 P1、 P 2 P_2 P2,二阶贝塞尔曲线的产生完全由这三个点的位置决定。
三个控制点每两个相邻的控制点产生一个一阶贝塞尔点,两个一阶贝塞尔点,于是得到两个点;
两个点形成一个线段,这个线段上有一个点在运动,于是得到一个点;
P 1 1 = ( 1 − t ) P 1 + t P 2 P 0 2 = ( 1 − t ) P 0 1 + t P 1 1 = ( 1 − t ) [ ( 1 − t ) P 0 + t P 1 ] + t [ ( 1 − t ) P 1 + t P 2 ] = P 0 ( 1 − t ) 2 + 2 P 1 t ( 1 − t ) + P 2 t 2 \begin{aligned} P_{1}^{1}&=\left( 1-t\right) P_{1}+tP_{2}\\ P_{0}^{2}&=\left( 1-t\right) P_{0}^{1}+tP_{1}^{1}\\ &=\left( 1-t\right) \left[ \left( 1-t\right) P_{0}+tP_{1}\right] +t\left[ \left( 1-t\right) P_{1}+tP_{2}\right] \\ &=P_{0}\left( 1-t\right) ^{2}+2P_{1}t\left( 1-t\right) +P_{2}t^{2} \end{aligned} P11P02=(1−t)P1+tP2=(1−t)P01+tP11=(1−t)[(1−t)P0+tP1]+t[(1−t)P1+tP2]=P0(1−t)2+2P1t(1−t)+P2t2
三阶贝塞尔曲线:
P 0 3 = P 0 ( 1 − t ) 3 + 3 P 1 t ( 1 − t ) + 3 P 2 t ( 1 − t ) + P 2 t 3 P_0^3=P_{0}\left( 1-t\right) ^{3}+3P_{1}t\left( 1-t\right) + 3P_{2}t\left( 1-t\right)+P_{2}t^{3} P03=P0(1−t)3+3P1t(1−t)+3P2t(1−t)+P2t3
通用递归定义公式:
P i k = { P i k = 0 ( 1 − t ) P i k − 1 + t P i + 1 k − 1 k ⩾ 1 P_{i}^{k}=\begin{cases} P_i&k=0\\ \left( 1-t\right) P_{i}^{k-1}+tP_{i+1}^{k-1}&k\geqslant1 \end{cases} Pik={Pi(1−t)Pik−1+tPi+1k−1k=0k⩾1
总结规律可得n阶贝塞尔曲线的公式为:
P i n = ∑ j = 0 n C n j ( 1 − t ) n − j t j P i + j t ∈ [ 0 , 1 ] P_{i}^{n}=\sum ^{n}_{j=0}C_{n}^{j}\left( 1-t\right) ^{n-j}t^{j}P_{i+j}\quad t\in[0,1] Pin=j=0∑nCnj(1−t)n−jtjPi+jt∈[0,1]
使用数学归纳法证明:
假设 n ⩽ k n\leqslant k n⩽k时如下等式成立
P i k = ∑ j = 0 k C k j ( 1 − t ) k − j t j P i + j P_{i}^{k}=\sum ^{k}_{j=0}C_{k}^{j}\left( 1-t\right) ^{k-j}t^{j}P_{i+j} Pik=j=0∑kCkj(1−t)k−jtjPi+j
当 n = k + 1 n=k+1 n=k+1时,
P i k + 1 = ( 1 − t ) P i k + t P i + 1 k . = ( 1 − t ) ∑ j = 0 k C k j ( 1 − t ) k − j t j P i + j + t ∑ j = 0 k C k j ( 1 − t ) k − j t j P i + j + 1 = ∑ j = 0 k C k j ( 1 − t ) k − j + 1 t j P i + j + ∑ j = 1 k + 1 C k j − 1 ( 1 − t ) k − j + 1 t j P i + j = ( 1 − t ) k + 1 + [ ∑ j = 1 k ( C k j + C k j − 1 ) ( 1 − t ) k − j + 1 t j P i + j ] + C k k t k + 1 \begin{aligned} P_{i}^{k+1}&=\left( 1-t\right) P_{i}^{k}+tP_{i+1}^{k}.\\ &=\left( 1-t\right) \sum ^{k}_{j=0}C_{k}^{j}\left( 1-t\right) ^{k-j}t^{j}P_{i+j}+t\sum ^{k}_{j=0}C_{k}^{j}\left( 1-t\right) ^{k-j}t^{j}P_{i+j+1}\\ &=\sum ^{k}_{j=0}C_{k}^{j}\left( 1-t\right) ^{k-j+1}t^{j}P_{i+j}+\sum ^{k+1}_{j=1}C_{k}^{j-1}\left( 1-t\right) ^{k-j+1}t^{j}P_{i+j} \\ &=\left( 1-t\right) ^{k+1}+\left[ \sum ^{k}_{j=1}\left( C_{k}^{j}+C_{k}^{j-1}\right) \left( 1-t\right) ^{k-j+1}t^{j}P_{i+j}\right] +C_{k}^{k}t^{k+1} \end{aligned} Pik+1=(1−t)Pik+tPi+1k.=(1−t)j=0∑kCkj(1−t)k−jtjPi+j+tj=0∑kCkj(1−t)k−jtjPi+j+1=j=0∑kCkj(1−t)k−j+1tjPi+j+j=1∑k+1Ckj−1(1−t)k−j+1tjPi+j=(1−t)k+1+[j=1∑k(Ckj+Ckj−1)(1−t)k−j+1tjPi+j]+Ckktk+1
因为
C k + 1 j = ( k + 1 ) ! ( k + 1 − j ) ! j ! C k j = k ! ( k − j ) ! j ! C k j − 1 = k ! ( k − j + 1 ) ! ( j − 1 ) ! C k j + C k j − 1 = k ! ( k − j ) ! ( j − 1 ) ! ( 1 j + 1 k − j + 1 ) = k ! ⋅ ( k + 1 ) [ ( k − j ) ! ⋅ ( k − j + 1 ) ] ⋅ [ ( j − 1 ) ! ⋅ j ] = ( k + 1 ) ! ( k + 1 − j ) ! j ! = C k + 1 j \begin{aligned} C_{k+1}^{j}&=\dfrac{\left( k+1\right) !}{\left( k+1-j\right) !j!}\\ C_{k}^{j}&=\dfrac{k!}{\left( k-j\right) !j!} \\ C_{k}^{j-1}&=\dfrac{k!}{\left( k-j+1\right) !\left( j-1\right) !} \\ C_{k}^{j}+C_{k}^{j-1}&=\dfrac{k!}{\left( k-j\right) !\left( j-1\right) !}\left( \dfrac{1}{j}+\dfrac{1}{k-j+1}\right) \\ &=\dfrac{k!\cdot \left( k+1\right) }{\left[ \left( k-j\right) !\cdot \left( k-j+1\right) \right] \cdot \left[ \left( j-1\right) !\cdot j\right] }\\ &=\dfrac{\left( k+1\right) !}{\left( k+1-j\right) !j!}=C_{k+1}^{j} \end{aligned} Ck+1jCkjCkj−1Ckj+Ckj−1=(k+1−j)!j!(k+1)!=(k−j)!j!k!=(k−j+1)!(j−1)!k!=(k−j)!(j−1)!k!(j1+k−j+11)=[(k−j)!⋅(k−j+1)]⋅[(j−1)!⋅j]k!⋅(k+1)=(k+1−j)!j!(k+1)!=Ck+1j
所以
P i k + 1 = ∑ j = 0 k + 1 C k + 1 j ( 1 − t ) k − j + 1 t j P i + j P_{i}^{k+1}=\sum ^{k+1}_{j=0} C_{k+1}^{j} \left( 1-t\right) ^{k-j+1}t^{j}P_{i+j} Pik+1=j=0∑k+1Ck+1j(1−t)k−j+1tjPi+j
贝塞尔曲线的性质:
- 各项系数之和为1
∑ j = 0 n C n j ( 1 − t ) n − j t j = ( 1 − t + t ) n = 1 \sum ^{n}_{j=0}C_{n}^{j}\left( 1-t\right) ^{n-j}t^{j}=(1-t + t)^n=1 j=0∑nCnj(1−t)n−jtj=(1−t+t)n=1 - 凸包性
由性质1可知贝塞尔曲线是控制点的凸组合,所以贝塞尔曲线始终包含在所有控制点组成的最小凸多边形中。也就是可以通过控制点的凸包来限制规划曲线的范围,这在路径规划中是很好的一条性质。 - 端点性质
第一个控制点和最后一个控制点,恰好是曲线的起始点和终止点。可以将 t = 1 t=1 t=1或 0 0 0代入,除了起始点和终止点的其他控制点的系数都是0。 - 一阶导数性质:贝塞尔曲线在 t = 0 t=0 t=0时的导数与 P i P i + 1 P_iP_{i+1} PiPi+1方向相同,在 t = 1 t=1 t=1时的导数与 P i + n − 1 P i + n P_{i+n-1}P_{i+n} Pi+n−1Pi+n方向相同
d P i n d t = d ( 1 − t ) n d t P i + ∑ j = 1 n − 1 C n j P i + j [ ( 1 − t ) n − j d t j d t + d ( 1 − t ) n − j d t t j ] + d t n d t P n = − n ( 1 − t ) n − 1 P i + n t n − 1 P i + n + ∑ j = 1 n − 1 C n j P i + j [ j ( 1 − t ) n − j t j − 1 − ( n − j ) ( 1 − t ) n − j − 1 t j ] \begin{aligned} \dfrac{{\rm d}P_{i}^{n}}{{\rm d}t}&=\dfrac{{\rm d}\left( 1-t\right) ^{n}}{{\rm d}t}P_{i}+\sum^{n-1}_{j=1}C_{n}^{j}P_{i+j}\left[ \left( 1-t\right) ^{n-j}\dfrac{{\rm d}t^{j}}{{\rm d}t}+\dfrac{{\rm d}\left( 1-t\right) ^{n-j}}{{\rm d}t}t^{j}\right] +\dfrac{{\rm d}t^{n}}{{\rm d}t}P_{n}\\ &=-n\left( 1-t\right) ^{n-1}P_{i}+nt^{n-1}P_{i+n}+\sum ^{n-1}_{j=1}C_{n}^{j}P_{i+j}\left[ j\left( 1-t\right) ^{n-j}t^{j-1}-\left( n-j\right) \left( 1-t\right) ^{n-j-1}t^{j}\right] \end{aligned} dtdPin=dtd(1−t)nPi+j=1∑n−1CnjPi+j[(1−t)n−jdtdtj+dtd(1−t)n−jtj]+dtdtnPn=−n(1−t)n−1Pi+ntn−1Pi+n+j=1∑n−1CnjPi+j[j(1−t)n−jtj−1−(n−j)(1−t)n−j−1tj]
d P i n d t ∣ t = 0 = − n P i + C n 1 P i + 1 = n ( P i + 1 − P i ) d P i n d t ∣ t = 1 = n P i + n − C n n − 1 P i + n − 1 = n ( P i + n − P i + n − 1 ) \begin{aligned} \dfrac{{\rm d}P_{i}^{n}}{{\rm d}t}| _{t=0}&=-nP_{i}+C_{n}^{1}P_{i+1}=n\left( P_{i+1}-P_{i}\right) \\ \dfrac{dP_i^{n}}{dt}| _{t=1}&=nP_{i+n}-C_{n}^{n-1}P_{i+n-1}=n\left( P_{i+n}-P_{i+n-1}\right) \end{aligned} dtdPin∣t=0dtdPin∣t=1=−nPi+Cn1Pi+1=n(Pi+1−Pi)=nPi+n−Cnn−1Pi+n−1=n(Pi+n−Pi+n−1)
分段贝塞尔曲线
虽然贝塞尔曲线的阶数可以很高,但是如果曲线的阶数过高,调整控制点对曲线的影响就比较小,调整起来相当麻烦。
于是,我们常常使用分段的贝塞尔曲线,保证每一小段不会太复杂。这样每次只用调小段,还可以做到只调局部不影响大局,那就相当舒服了。
分段带来的唯一问题是,曲线在段与段的交界处,如何保证平滑?
所谓平滑,其实就是一阶导数连续,也就是左右导数的极限相同。
对两侧的贝塞尔曲线求导,分别代入 t=0 和 t=1 (即贝塞尔曲线的开始和结束时间),让二者相等。此时能发现,当两侧控制点与分段交接点共线且形成的线段长度相等时,满足曲线平滑性质。
参考资料
B样条曲线
样条曲线
设 [ a , b ] [a,b] [a,b]为 R \mathbb{R} R上的区间
样条是通过一组指定点集而生成平滑曲线的柔性带。 简单地说,B 样条曲线就是通过控制点局部控制形状的曲线。
贝塞尔曲线有以下缺陷:
- 确定了多边形的顶点数(n+1个),也就决定了所定义的Bezier曲线的阶次(n次),这样很不灵活。
- 当顶点数(n+1)较大时,曲线的次数较高,曲线的导数次数也会较高,因此曲线会出现较多的峰谷值。
- 贝塞尔曲线无法局部修改。
B样条曲线除了保持Bezier曲线所具有的优点外,还弥补了上述所有的缺陷。
样条曲线的次数是指在指定区间上是几次多项式,阶数是指样条曲线有几阶连续导数。k阶B样条=关于u的k-1次曲线
设有P,P,P,…,P一共n+1个控制点,这些控制点用于定义样条曲线的走向、界限范围,则k阶B样条曲线的定义为:
P ( u ) = [ P 0 P 1 ⋯ P n ] [ B 0 , k ( u ) B 1 , k ( u ) ⋮ B n , k ( u ) ] = ∑ i = 0 n P i B i , k ( u ) P(u)=\begin{bmatrix} P_0&P_1&\cdots&P_n\end{bmatrix} \begin{bmatrix} B_{0,k}(u)\\ B_{1,k}(u)\\ \vdots\\ B_{n,k}(u) \end{bmatrix}= \sum_{i=0}^n P_i B_{i,k}(u) P(u)=[P0P1⋯Pn]⎣⎢⎢⎢⎡B0,k(u)B1,k(u)⋮Bn,k(u)⎦⎥⎥⎥⎤=i=0∑nPiBi,k(u)
式中, B i , k ( u ) B_{i,k}(u) Bi,k(u)是第i个k阶B样条基函数,与控制点 P i P_i Pi相对应,u是自变量。
基函数有如下德布尔-考克斯递推式:
B i . k ( u ) = { { 1 , u i ⩽ u < u i + 1 0 , o t h e r k = 1 u − u i u i + k − 1 − u i B i , k − 1 ( u ) + u i + k − u u i + k − u i + 1 B i + 1 , k − 1 ( u ) k ⩾ 2 B_{i.k}(u)= \begin{cases} \begin{cases} 1,&u_i\leqslant u
约定 0 / 0 = 0 0/0=0 0/0=0,式中 u i u_i ui是一组被称为节点矢量的非递减序列的连续变化值,首末值一般定义为0和1,该序列如下:
[ u 0 , u 1 , ⋯ , u k , u k + 1 , ⋯ , u n , u n + 1 , ⋯ , u n + k ] \left[u_0,u_1,\cdots,u_k,u_{k+1},\cdots,u_n,u_{n+1},\cdots,u_{n+k}\right] [u0,u1,⋯,uk,uk+1,⋯,un,un+1,⋯,un+k]