机器学习——SVM

一、SVM介绍

SVM(Support Vector Machine)指的是支持向量机，是常见的一种判别方法。在机器学习领域，是一个有监督的学习模型，通常用来进行模式识别、分类以及回归分析。它在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够推广应用到函数拟合等其他其他问题中。
支持向量机（Support Vector Machine, SVM）是一类按监督学习（supervised learning）方式对数据进行二元分类（binary classification）的广义线性分类器（generalized linear classifier），其决策边界是对学习样本求解的最大边距超平面（maximum-margin hyperplane)。

二、SVM原理

1.SVM的主要特点：
SVM主要思想是针对两类分类问题，在高维空间中寻找一个超平面作为两类的分割，以保证最小的分类错误率。
SVM考虑寻找一个满足分类要求的超平面，并且使训练集中的点距离分类面尽可能的远，即寻找一个分类面使它两侧的空白区域(margin)最大。
过两类样本中离分类面最近的点且平行于最优分类面的超平面上的训练样本就叫做支持向量。
最优分类面就是要求分类线不但能将两类正确分开(训练错误率为0)，且使分类间隔最大。

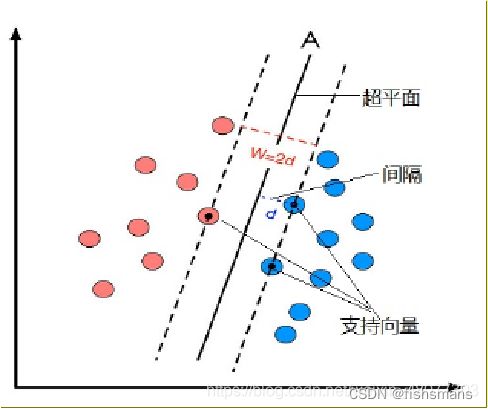
2.1 超平面推导
在 (xi, yi) 中，我们用 xi 表示了点的坐标，yi 表示了分类结果。超平面表示如下：

在超平面的上方的点满足：

在超平面的下方的点满足：

因为 yi 只有两种取值 1 和 -1。因此就满足：
整合这两个等式（左右都乘以 yi，当yi是负值时，不等号要改方向）得：
2.2支持向量
所有坐落在边界的边缘上的点被称作是 “支持向量”。分界边缘上的任意一点到超平面的距离为:

其中，||w|| 是向量的范数(norm)，或者说是向量的模。它的计算方式为：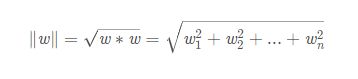
所以最大边界距离为

3.约束条件

• 并不是所有的方向都存在能够实现100%正确分类的分类超平面，如何判断一条直线是否能够将所有的样本点都正确分类？
• 即便找到了正确的超平面方向，还要注意分类超平面的位置应该在间隔区域的中轴线上，所以用来确定分类超平面位置的截距b也不能随意的取值，而是受到分类超平面方向和样本点分布的约束。
• 即便取到了合适的方向和截距，该如何找到对应的支持向量来计算距离d？
  以二维分类为例：平面上有2种颜色的点，红色和蓝色，我们对它们进行标记，红色圆点标记为1，为正样本；蓝色五角星标记为-1，为负样本。则该模型可以表示为：
  
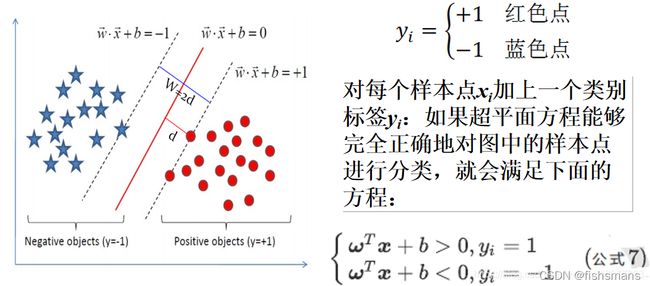
  我们假设我们所绘制的直线正好处于分类间隔的中轴线上，且对应的支持向量对应的样本点到直线的距离为d则公式可表示为：
  接着我们就可以对表达式进行化简。

三、SVM的应用举例

使用sklearn中的包对iris数据进行分类
http://scikit-learn.org/dev/modules/svm.html#svm-classification

#!/usr/bin/python
# -*- coding:utf-8 -*-
 
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
 
 
if __name__ == "__main__":
    iris_feature = '花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度'
    path = './iris.data'  # 数据文件路径
    data = pd.read_csv(path, header=None)
    x, y = data[[0, 1]], pd.Categorical(data[4]).codes
    x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1, train_size=0.6)
 
    # 分类器
    clf = svm.SVC(C=0.1, kernel='linear', decision_function_shape='ovr')
    # clf = svm.SVC(C=0.8, kernel='rbf', gamma=20, decision_function_shape='ovr')
    clf.fit(x_train, y_train.ravel())
 
    # 准确率
    print(clf.score(x_train, y_train))  # 精度
    print('训练集准确率：', accuracy_score(y_train, clf.predict(x_train)))
    print(clf.score(x_test, y_test))
    print('测试集准确率：', accuracy_score(y_test, clf.predict(x_test)))
 
    # decision_function
    print(x_train[:5])
    print('decision_function:\n', clf.decision_function(x_train))
    print('\npredict:\n', clf.predict(x_train))
 
    # 画图
    x1_min, x2_min = x.min()
    x1_max, x2_max = x.max()
    x1, x2 = np.mgrid[x1_min:x1_max:500j, x2_min:x2_max:500j]  # 生成网格采样点
    grid_test = np.stack((x1.flat, x2.flat), axis=1)  # 测试点
    grid_hat = clf.predict(grid_test)       # 预测分类值
    grid_hat = grid_hat.reshape(x1.shape)  # 使之与输入的形状相同
    mpl.rcParams['font.sans-serif'] = ['SimHei']
    mpl.rcParams['axes.unicode_minus'] = False
 
    cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
    cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
    plt.figure(facecolor='w')
    plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)
    plt.scatter(x[0], x[1], c=y, edgecolors='k', s=50, cmap=cm_dark)      # 样本
    plt.scatter(x_test[0], x_test[1], s=120, facecolors='none', zorder=10)     # 圈中测试集样本
    plt.xlabel(iris_feature[0], fontsize=13)
    plt.ylabel(iris_feature[1], fontsize=13)
    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)
    plt.title('鸢尾花SVM二特征分类', fontsize=16)
    plt.grid(b=True, ls=':')
    plt.tight_layout(pad=1.5)
    plt.show()