目标检测中边框回归的直观理解 bbox regression

目录

1 摘要

2 算法要解决的问题

3 从结果推原因，算法的实现思路

3.1 最直接的实现

3.2 合理性讨论

4 CNN的尺度不变性的影响

4.1 log函数的非线性问题

5 线性模型的损失函数

5.1 预测参数

5.2 线性模型的损失

5.3 线性模型的目标函数

---

1 摘要

一般的目标检测算法的目的是在原图上生成若干个边界矩形框，bounding box（bbox），要求是生成的bbox尽可能的不多不少刚好完整包裹住目标物体。我们可以用一些方法来生候选边框，并且将这些候选框进行分类检测，将除了背景以外的框保留作为我们的输出。这些不在本文的重点关注内容里。本文关注的是当筛选出含有目标物体的边框之后，边框位置的精修问题。

本文中对算法说明的顺序可能和其他文章不同，我希望从更加直观的角度去理解这个算法。本文的算法以RCNN实现的bbox回归为参考。

2 算法要解决的问题

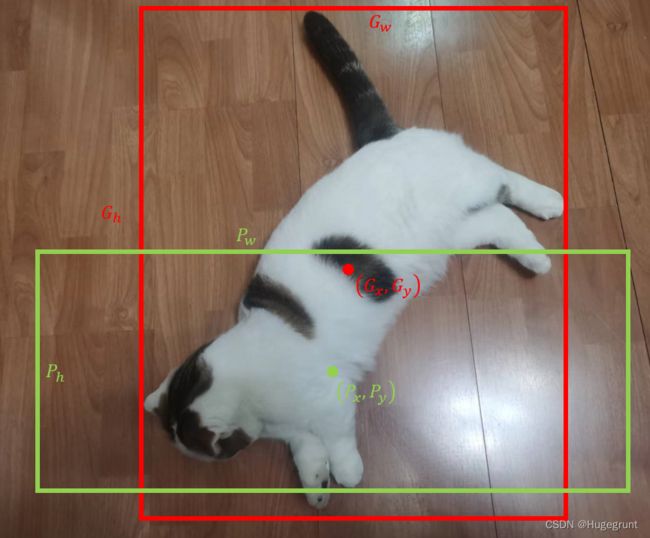
比如说下图中用绿框来表示筛选出来的bbox，红框表示真实的bbox。从直观来看，两个边框都包含了“猫”的元素。所以在算法中很可能也会将绿框视为一个猫的目标物体框。但是我们可以明显的看出，绿框和红框的形状和位置差距很大。真实的检测场景下我们应该是期待算法检测出一个和红框更相似的边框出来。

这时，实践证明我们可以用一个所谓的bbox 回归算法来对绿框进行校正和精修来生成一个新的检测框，这个新的检测框应该尽可能的和红色的检测框相似。

3 从结果推原因，算法的实现思路

首先不得不说，发明或者发现这些算法的人是非常杰出的。作为常人我们可能暂时没有那么强的头脑或者运气来发现或者发明这些算法，我们也很难去揣摩这些算法的原始作者们如何想到这些天才的主意的。但是我们至少可以根据常识来对这些算法如何实现以及如何变得有效做一下逆向的推理或者解释。

3.1 最直接的实现

上文提到，我们可以使用回归的算法来对绿框进行精修。按照构建线性回归模型最直接的方式是，我们建立一个模型，然后让这个模型输出四个值，一个是矩形框的左上坐标x0，y0.另外一个是右下角的坐标x1，y1（我们暂且叫它们为一组对角坐标，建立一个向量（x0，y0，x1，y1）叫对角坐标向量，名字是我自己瞎起的）。然后我们要做的是用真实的边框对角坐标向量和预测的对角坐标向量求方差作为损失来对回归模型做训练。

那模型的输入应该是什么呢？应该是图片的特征，一般目标检测算法都有CNN网络来提取图片特征，我们可以把这些提取出的特征输入到这个线性回归模型里面。

3.2 合理性讨论

但这种方式好像看上去有点别扭，我们再往上看一层，CNN输出的特征到底是什么。CNN输出的特征应该是候选边框（也就是前文图中的绿框）经过CNN网络抽取的特征。上面提到的方法实质上是根据这些特征来找到一组对角坐标这组坐标看上去和绿框的坐标本身没有什么联系，好像就是凭空生成的，虽然机器学习算法很强大，但也应该思考需不需要选择逻辑上更加合理的模型构建的方式。

于是我们可以开下脑洞，假设绿框（回归前的bbox框）和红框（真实边框）是存在某种转换关系的。因为绿框和红框包含同一个信息（猫），而且我们通过验证（使用IOU方法）发现其实绿框和红框都是定位到一个物体上。那我们就可以假设这种转换关系是非常简单的仿射转换关系。绿框捕捉到的信息就是将红框内容平移并且缩放一下。那我们可以根据绿框中我们已经找到的信息来推理出来真实的边框应该是什么样子的。举个例子比如上上面我们采到了一个绿框检测到了一只猫，但是通过学习，我们知道这个绿框内图片的特征是 首先在正常猫目标框宽度方向多了一些背景，另外在高度方向少了“猫尾巴”。要补全这个绿框我们大概率应该在两边砍掉一些，并在高度方向增加一些。

那么回归模型的输入不变，还是图像的特征，但模型的输出可以调整下来让模型更加合理。输出改为模型的平移参数和缩放参数。

这时又产生一个新的问题，如何表示平移和缩放？

首先我们换一种表示边框的方式，舍弃对角坐标向量的表示法。换成一种中心点坐标+宽高的四维向量。真实的bbox我们叫它ground truth，记为, 预测的bbox向量记为。

 这时候大家会想我们可以设定一组对做简单加法，再找出一组对做乘法。我们只需要建立对真实的回归模型就行了。到这里我们已经很接近了，但还需要一些工作和思考，这样简单的构建转换关系真的可以吗？

4 CNN的尺度不变性的影响

我们先来看一看如果我们手上有一个能够输出的线性模型，并且通过训练，对上文中插图非常有效。即我将一绿框部分区域图片输入给一个CNN网络，这个网络输出了一组图片特征，记为一个特征向量。将输入到线性模型当中，模型就会输出一组令绿框变换后成为红框或者接近红框。但此时如果我们将绿框内图像缩小之后再进行相同的操作会发生什么？因为CNN的尺度不变性，图像缩小后输入到CNN网络提取出的特征向量应该也是（实际上因为缩放后略微失真可能特征向量会有微小差异，但本文不做严谨性讨论，主要关注在理解算法思路）这个将不会包含任何尺寸相关的特征，将这个输入到线性模型后输出的应该也和前面的一样。显然，如果这个缩小后的图像再使用同一组变换参数进行转换的话是得不出正确的边框的。

那我们可以修改一下。将上面的参数标准化一下，令线性模型的输出除以预测的矩形框的大小，变为。这里有一个数学小技巧，就是缩放的倍率应该是大于零的，但是线性模型的输出是在实数域上面的，所以可以将预测的缩放倍率参数做一下转化改为：。这四个参数就应该是我们线性模型最终的输出，这四个参数的真实值记为。

4.1 log函数的非线性问题

这里简单提下log函数的非线性问题，我们线性回归的对象最终为缩放倍率的对数，这显然引入了非线性因素，举个不严谨但是很形象的例子。我有两个预测出来的目标范围框，第一个框里面的区域图片我检测“猫尾巴”的特征是1/4代表我只截取到了1/4个猫尾巴，第二个框里面“猫尾巴”的特征为1/2代表截取了1/2个毛尾巴，而真实框中应该有1整个猫尾巴。那么在检测框中心点已经对准的情况下第一个框应该扩大四倍，第二个框应该扩大两倍，这种线性特性正好可以通过线性模型预测出来。但是加上log之后扩大倍率的参数就变成“非线性”的了。按理说使用线性模型的效果就不会很好了。但因为上文也说过，待调整的绿框也是经过筛选的，它们和真实红框的差距不应该过大（以IOU衡量），那么实际上可以理解为缩放的比例应该在1附近(这里“附近”只是定性的概念，实际上衡量绿框和红框相似度的方式并不能一定直接能保证缩放比例在1附近，比如IOU关注的就是面积重合的程度，并不直接关注缩放比例的大小。不过实验证明这种方式有效，我们还是可以这样理解)。根据简单的高等数学，对于log（x），x在1附近时, 我们可以用线性函数来近似。这就说明了为什么就算缩放比例加了log我们还是可以有效地用线性模型来进行回归。

5 线性模型的损失函数

 通过上面的分析，我们可以根据预测框和真实框的位置尺寸计算出真实的转换参数。

5.1 预测参数

首先我们有一个待优化的边框记为,将原图中P区域抠出来的图像输入到目标检测系统的CNN网络中，得出一个特征向量，我们把这个特征向量视为P经过一个由抠图+CNN的函数转换得来的向量，记为然后将该向量输入到线性回归模型中，假设线性回归模型的参数为,那么模型的输出为。

5.2 线性模型的损失

模型的损失函数应该为真实值和预测值的方差，即

5.3 线性模型的目标函数

将损失加上正则化就是目标函数了，我们优化的目标是找到，使得目标函数最小化,表示为