李沐动手学深度学习V2-NLP序列模型和代码实现

一. 序列模型

1. 统计工具

处理序列数据需要统计工具和新的深度神经网络架构，如下图股票价格示例所示，其中用$x_t$表示价格，即在时间步（time step）$t\in {\mathbb{Z}}^{+}$时，观察到的价格$x_t$。注意$t$对于本文中的序列通常是离散的，并在整数或其子集上变化。假设一个交易员想在$t$日的股市中表现良好，于是通过以下途径预测$x_t$：
$$x_t\sim P(x_t\mid x_{t-1},\dots ,x_1).$$

2. 自回归模型

为了实现这个预测，交易员可以使用回归模型，但有个问题：输入数据的数量，输入$x_{t-1},\dots ,x_1$本身因$t$而异。也就是说，输入数据的数量这个数字将会随着遇到的数据量的增加而增加，因此需要一个近似方法来使这个计算变得容易处理。本节后面的大部分内容将围绕着如何有效估计
$P(x_t\mid x_{t-1},\dots ,x_1)$展开。
简单地说，它归结为以下两种策略：

• 第一种策略，假设在现实情况下相当长的序列$x_{t-1},\dots ,x_1$可能是不必要的，因此只需要满足某个长度为$\tau$的时间跨度，也即是使用观测序列$x_{t-1},\dots ,x_{t-\tau }$，好处就是输入参数的数量总是不变的，至少在$t>\tau$时如此，这就使能够训练一个上面提及的深度网络，这种模型被称为自回归模型（autoregressive models），因为它们是对自己执行回归。
• 第二种策略，如下图所示所示，保留一些对过去观测的总结$h_t$，并且同时更新预测${\hat{x}}_t$和总结$h_t$。这就产生了基于${\hat{x}}_t=P(x_t\mid h_t)$估计$x_t$，以及公式$h_t=g(h_{t-1},x_{t-1})$更新的模型。由于$h_t$从未被观测到，这类模型也被称为隐变量自回归模型（latent autoregressive models）。
  

整个序列的估计值都将通过以下的方式获得：
$$P(x_1,\dots ,x_T)=\prod _{t=1}^{T}P(x_t\mid x_{t-1},\dots ,x_1).$$
注意如果处理的是离散的对象（如单词）而不是连续的数字，需要使用分类器而不是回归模型来估计$P(x_t\mid x_{t-1},\dots ,x_1)$。

3. 马尔可夫模型

回想一下在自回归模型的近似法中，使用$x_{t-1},\dots ,x_{t-\tau }$ 而不是$x_{t-1},\dots ,x_1$来估计$x_t$。只要这种是近似精确的，就说序列满足马尔可夫条件（Markov condition）。特别是，如果$\tau =1$，得到一个
一阶马尔可夫模型（first-order Markov model），$P(x)$由下式给出：
$$P(x_1,\dots ,x_T)=\prod _{t=1}^{T}P(x_t\mid x_{t-1})\text{ 当 }P(x_1\mid x_0)=P(x_1).$$
当假设$x_t$仅是离散值时，这样的模型特别好，因为在这种情况下，使用动态规划可以沿着马尔可夫链精确地计算结果。例如，可以高效地计算$P(x_{t+1}\mid x_{t-1})$：
$$\begin{array}{rl}P(x_{t+1}\mid x_{t-1})& =\frac{{\sum }_{x_t}P(x_{t+1},x_t,x_{t-1})}{P(x_{t-1})}\\ & =\frac{{\sum }_{x_t}P(x_{t+1}\mid x_t,x_{t-1})P(x_t,x_{t-1})}{P(x_{t-1})}\\ & =\sum _{x_t}P(x_{t+1}\mid x_t)P(x_t\mid x_{t-1})\end{array}$$
利用这一事实，只需要考虑过去观察中的一个非常短的历史：$P(x_{t+1}\mid x_t,x_{t-1})=P(x_{t+1}\mid x_t)$。

4. 因果关系

原则上，将$P(x_1,\dots ,x_T)$倒序展开也没什么问题，毕竟，基于条件概率公式，总是可以写出：
$$P(x_1,\dots ,x_T)=\prod _{t=T}^{1}P(x_t\mid x_{t+1},\dots ,x_T).$$
事实上，如果基于一个马尔可夫模型，可以得到一个反向的条件概率分布。然而在许多情况下，数据存在一个自然的方向，即在时间上是前进的。很明显，未来的事件不能影响过去。因此，如果改变$x_t$，可能会影响未来发生的事情$x_{t+1}$，但不能反过来。也就是说，如果改变$x_t$，基于过去事件得到的分布不会改变。因此，解释$P(x_{t+1}\mid x_t)$应该比解释$P(x_t\mid x_{t+1})$更容易。例如，在某些情况下，对于某些可加性噪声$ϵ$，显然可以找到$x_{t+1}=f(x_t)+ϵ$，而反之则不行。

5. 训练

5.1 首先生成一些数据：使用正弦函数和一些可加性噪声来生成序列数据， 生成了1000个数据

import d2l.torch
import torch
from torch import nn
T = 1000 # 总共产生1000个点
time = torch.arange(1,T+1,dtype=torch.float32)
X = torch.sin(0.01*time)+torch.normal(0,0.2,(T,))
d2l.torch.plot(time,X,'time','x',xlim=[1,1000],figsize=(6,3))

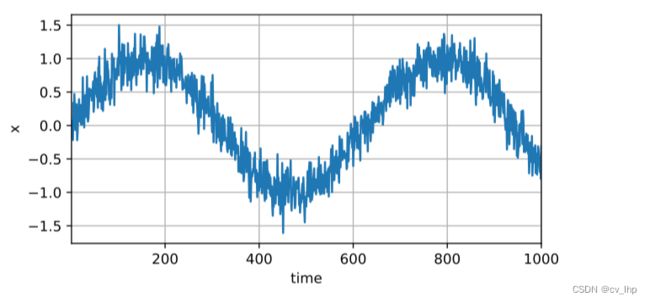
5.2 接下来，将这个序列转换为模型的“特征－标签”（feature-label）对。基于嵌入维度$\tau$，将数据映射为数据对$y_t=x_t$和${\mathbf{x}}_t=[x_{t-\tau },\dots ,x_{t-1}]$。 这比提供的数据样本少了 个， 因为没有足够的历史记录来描述前 个数据样本。 一个简单的解决办法是：如果拥有足够长的序列就丢弃这几项； 另一个方法是用零填充序列。 在这里仅使用前600个“特征－标签”对进行训练。

tau = 4
features = torch.zeros(size=(T-tau,tau))
for i in range(tau):
    features[:,i] = X[i:T-tau+i]
lables = X[tau:].reshape(-1,1)
batch_size,n_train = 16,600
# 只有前n_train个样本用于训练
train_iter = d2l.torch.load_array((features[:n_train],lables[:n_train]),batch_size,is_train=True)

5.3 使用一个简单的架构训练模型： 一个拥有两个全连接层的多层感知机，ReLU激活函数和平方损失。

# 初始化网络权重的函数
def init_weight(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform_(m.weight)
# 一个简单的多层感知机
def get_net():
    net = nn.Sequential(nn.Linear(4,10),
                        nn.ReLU(),
                        nn.Linear(10,1))
    return net
# 平方损失。注意：MSELoss计算平方误差时不带系数1/2
loss = nn.MSELoss(reduction='none')

5.4 开始训练模型

def train(net,train_iter,loss,epochs,lr):
    optim = torch.optim.Adam(net.parameters(),lr=lr)
    for epoch in range(epochs):
        for X,y in train_iter:
            optim.zero_grad()
            y_hat = net(X)
            ls = loss(y_hat,y)
            ls.sum().backward()
            optim.step()
        print(f'epoch:{epoch+1}',f'total loss:{d2l.torch.evaluate_loss(net,train_iter,loss)}')
net = get_net()
train(net,train_iter,loss,50,0.03)

5.5 由于训练损失很小，下面进行模型预测下一个时间步的能力， 也就是单步预测（one-step-ahead prediction），预测结果如下图所示。

onestep_preds = net(features)
d2l.torch.plot([time,time[tau:]],[X.detach().numpy(),onestep_preds.detach().numpy()],'time','x',legend=['x','onestep_preds'],xlim=[1,1000],figsize=(6,3))

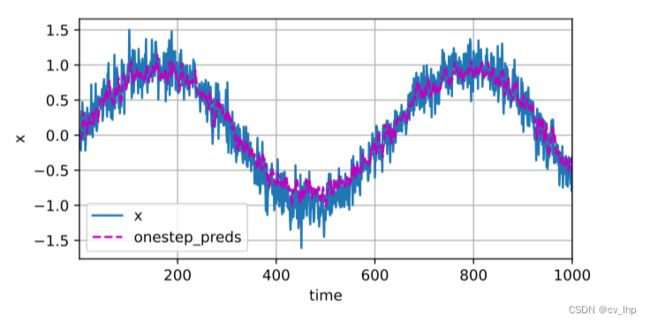
5.6 多步预测：使用程序的预测值（而不是原始数据）来进行多步预测，如下图所示。
$$\begin{gathered} {\hat{x}}_{605}=f(x_{601},x_{602},x_{603},x_{604}), \\ {\hat{x}}_{606}=f(x_{602},x_{603},x_{604},{\hat{x}}_{605}), \\ {\hat{x}}_{607}=f(x_{603},x_{604},{\hat{x}}_{605},{\hat{x}}_{606}), \\ {\hat{x}}_{608}=f(x_{604},{\hat{x}}_{605},{\hat{x}}_{606},{\hat{x}}_{607}), \\ {\hat{x}}_{609}=f({\hat{x}}_{605},{\hat{x}}_{606},{\hat{x}}_{607},{\hat{x}}_{608}), \\ \dots \end{gathered}$$

multistep_preds = torch.zeros(T)
multistep_preds[:n_train+tau] = X[:n_train+tau]
for i in range(n_train+tau,T):
    multistep_preds[i] = net(multistep_preds[i-tau:i].reshape(1,-1)).reshape(-1)

d2l.torch.plot([time,time[tau:],time[n_train+tau:]],[X.detach().numpy(),onestep_preds.detach().numpy(),multistep_preds[n_train+tau:].detach().numpy()],'time','x',legend=['x','onestep_preds','multistep_preds'],xlim=[1,1000],figsize=(6,3))

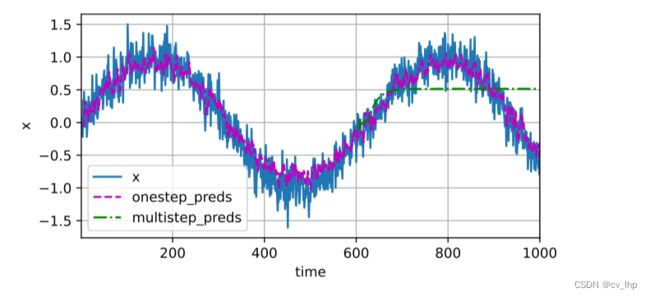
5.7 如多步预测结果所示，绿线的预测显然并不理想，经过几个预测步骤之后，预测的结果很快就会衰减到一个常数，因为由于错误的累积：假设在步骤$1$之后，积累了一些错误${ϵ}_1=\overline{ϵ}$，步骤$2$的输入被扰动了${ϵ}_1$，结果积累的误差是依照次序的${ϵ}_2=\overline{ϵ}+c{ϵ}_1$，其中$c$为某个常数，后面的预测误差依此类推。因此误差可能会相当快地偏离真实的观测结果。例如未来$24$小时的天气预报往往相当准确，但超过这一点，精度就会迅速下降。基于$k=1,4,16,64$，通过对整个序列预测的计算，看一下k步预测的结果，如下图所示。

max_steps = 64
features = torch.zeros((T-tau-max_steps+1,tau+max_steps))
for i in range(tau):
    features[:,i] = X[i:i+T-tau-max_steps+1]
for i in range(tau,tau+max_steps):
    features[:,i] = net(features[:,i-tau:i]).reshape(-1)
steps = (1,4,16,64)
#steps表示是根据4个观察到的时序数据来预测接下来后面的64个值，然后打印这预测64个值中预测的第一个值，第4个值，第16个值，第64个值
d2l.torch.plot([time[tau+i-1:i+T-max_steps] for i in steps],[features[:,(tau+i-1)].detach().numpy() for i in steps],'time','x',legend=['1_step_preds','4_step_preds','16_step_preds','64_step_preds'],xlim=[1,1000],figsize=(6,3))

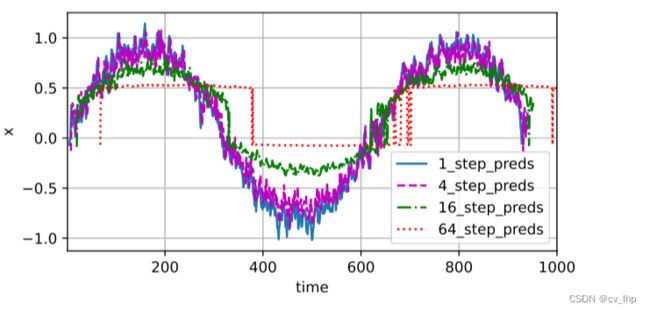
如上图所示说明了当试图预测更远的未来时，预测的质量是如何变化的，虽然“ 4 步预测”看起来不错，但超过这个跨度的任何预测几乎都是无用的。

6 小结

1. 内插法（在现有观测值之间进行估计）和外推法（对超出已知观测范围进行预测）在实践的难度上差别很大。因此，对于所拥有的序列数据，在训练时始终要尊重其时间顺序，即最好不要基于未来的数据进行训练。
2. 序列模型的估计需要专门的统计工具，两种较流行的选择是自回归模型和隐变量自回归模型。
3. 对于时间是向前推进的因果模型，正向估计通常比反向估计更容易。
4. 对于直到时间步 的观测序列，其在时间步 + 的预测输出是“ 步预测”。随着对预测时间 值的增加，会造成误差的快速累积和预测质量的极速下降。

7. 全部代码

import d2l.torch
import torch
from torch import nn
!nvidia-smi
!pwd
T = 1000
time = torch.arange(1, T + 1, dtype=torch.float32)
X = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,))
d2l.torch.plot(time, X, 'time', 'x', xlim=[1, 1000], figsize=(6, 3))
tau = 4
features = torch.zeros(size=(T - tau, tau))
for i in range(tau):
    features[:, i] = X[i:T - tau + i]
lables = X[tau:].reshape(-1, 1)
batch_size, n_train = 16, 600
# 只有前n_train个样本用于训练
train_iter = d2l.torch.load_array((features[:n_train], lables[:n_train]), batch_size, is_train=True)


# 初始化网络权重的函数
def init_weight(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform_(m.weight)


# 一个简单的多层感知机
def get_net():
    net = nn.Sequential(nn.Linear(4, 10),
                        nn.ReLU(),
                        nn.Linear(10, 1))
    return net


# 平方损失。注意：MSELoss计算平方误差时不带系数1/2
loss = nn.MSELoss(reduction='none')


def train(net, train_iter, loss, epochs, lr):
    optim = torch.optim.Adam(net.parameters(), lr=lr)
    for epoch in range(epochs):
        for X, y in train_iter:
            optim.zero_grad()
            y_hat = net(X)
            ls = loss(y_hat, y)
            ls.sum().backward()
            optim.step()
        print(f'epoch:{epoch + 1}', f'total loss:{d2l.torch.evaluate_loss(net, train_iter, loss)}')


net = get_net()
train(net, train_iter, loss, 50, 0.03)
onestep_preds = net(features)
d2l.torch.plot([time, time[tau:]], [X.detach().numpy(), onestep_preds.detach().numpy()], 'time', 'x',
               legend=['x', 'onestep_preds'], xlim=[1, 1000], figsize=(6, 3))
multistep_preds = torch.zeros(T)
multistep_preds[:n_train + tau] = X[:n_train + tau]
for i in range(n_train + tau, T):
    multistep_preds[i] = net(multistep_preds[i - tau:i].reshape(1, -1)).reshape(-1)

d2l.torch.plot([time, time[tau:], time[n_train + tau:]],
               [X.detach().numpy(), onestep_preds.detach().numpy(), multistep_preds[n_train + tau:].detach().numpy()],
               'time', 'x', legend=['x', 'onestep_preds', 'multistep_preds'], xlim=[1, 1000], figsize=(6, 3))
max_steps = 64
features = torch.zeros((T - tau - max_steps + 1, tau + max_steps))
for i in range(tau):
    features[:, i] = X[i:i + T - tau - max_steps + 1]
for i in range(tau, tau + max_steps):
    features[:, i] = net(features[:, i - tau:i]).reshape(-1)
steps = (1, 4, 16, 64)
#steps表示是根据4个观察到的时序数据来预测接下来后面的64个值，然后打印这预测64个值中预测的第一个值，第4个值，第16个值，第64个值
d2l.torch.plot([time[tau + i - 1:i + T - max_steps] for i in steps],
               [features[:, (tau + i - 1)].detach().numpy() for i in steps], 'time', 'x',
               legend=['1_step_preds', '4_step_preds', '16_step_preds', '64_step_preds'], xlim=[1, 1000],
               figsize=(6, 3))

8. 链接

循环神经网络RNN第一篇：李沐动手学深度学习V2-NLP序列模型和代码实现
循环神经网络RNN第二篇：李沐动手学深度学习V2-NLP文本预处理和代码实现
循环神经网络RNN第三篇：李沐动手学深度学习V2-NLP语言模型、数据集加载和数据迭代器实现以及代码实现
循环神经网络RNN第四篇：李沐动手学深度学习V2-RNN原理
循环神经网络RNN第五篇：李沐动手学深度学习V2-RNN循环神经网络从零实现
循环神经网络RNN第六篇：李沐动手学深度学习V2-使用Pytorch框架实现RNN循环神经网络
循环神经网络GRU第七篇：李沐动手学深度学习V2-GRU门控循环单元以及代码实现
循环神经网络LSTM第八篇：李沐动手学深度学习V2-LSTM长短期记忆网络以及代码实现
深度循环神经网络第九篇：李沐动手学深度学习V2-深度循环神经网络和代码实现
双向循环神经网络第十篇：李沐动手学深度学习V2-双向循环神经网络Bidirectional RNN和代码实现