pytorch损失函数总结
pytorch损失函数总结
本文主要介绍了pytorch中的一些损失函数:1. nn.L1Loss 2. nn.SmoothL1Loss 3. nn.MSELoss 4. nn.CrossEntropyLoss
1.nn.L1Loss
1.1 数学表达式
loss ( x i , y i ) = ∣ x i − y i ∣ \operatorname{loss}\left(x_{i}, y_{i}\right)=\left|x_{i}-y_{i}\right| loss(xi,yi)=∣xi−yi∣
1.2 代码
Examples::
>>> loss = nn.L1Loss(reduction='sum')
>>> input = torch.tensor([1., 2, 3, 4])
>>> target = torch.tensor([4., 5, 6, 7])
>>> output = loss(input, target)
>>> print(output)
1.3 说明
函数nn.L1Loss有一个参数reduction,reduction有三个参数分别是:none、sum、elementwise_mean,当reduction=none时,返回的是一个向量(batch_size)如tensor([3., 3., 3., 3.]);当reduction=sum时,函数返回的是tensor(12.);当reduction=elementwise_mean时,函数返回的是tensor(3.)
2.nn.SmoothL1Loss
2.1 数学表达式
loss ( x i , y i ) = { 1 2 ( x i − y i ) 2 if ∣ x i − y i ∣ < 1 ∣ x i − y i ∣ − 1 2 , otherwise \operatorname{loss}\left(\mathbf{x}_{i}, \mathbf{y}_{i}\right)=\left\{\begin{array}{cc} \frac{1}{2}\left(\mathbf{x}_{i}-\mathbf{y}_{i}\right)^{2} & \text { if }\left|\mathbf{x}_{i}-\mathbf{y}_{i}\right|<1 \\ \left|\mathbf{x}_{i}-\mathbf{y}_{i}\right|-\frac{1}{2}, & \text { otherwise } \end{array}\right. loss(xi,yi)={21(xi−yi)2∣xi−yi∣−21, if ∣xi−yi∣<1 otherwise
关于 x i − y i \mathbf{x}_{i}-\mathbf{y}_{i} xi−yi求导之后得到
loss ′ ( x i , y i ) = { x i − y i if ∣ x i − y i ∣ < 1 1 if x i − y i > 1 − 1 if x i − y i < − 1 \operatorname{loss}^{\prime}\left(\mathbf{x}_{i}, \mathbf{y}_{i}\right)=\left\{\begin{array}{cc} \mathbf{x}_{i}-\mathbf{y}_{i} & \text { if }\left|\mathbf{x}_{i}-\mathbf{y}_{i}\right|<1 \\ 1 & \text { if } \mathbf{x}_{i}-\mathbf{y}_{i}>1 \\ -1 & \text { if } \mathbf{x}_{i}-\mathbf{y}_{i}<-1 \end{array}\right. loss′(xi,yi)=⎩⎨⎧xi−yi1−1 if ∣xi−yi∣<1 if xi−yi>1 if xi−yi<−1
2.2 代码
import torch
import torch.nn as nn
import torch.nn.functional as F
a = torch.tensor([1., 2, 3, 4])
b = torch.tensor([1.1, 5, 6, 7])
loss_fn = nn.SmoothL1Loss(reduction='none')
loss = loss_fn(a, b)
print(loss)
#out
tensor([0.0050, 2.5000, 2.5000, 2.5000])
3.nn.MSELoss
3.1 数学表达式
loss ( x i , y i ) = ( x i − y i ) 2 \operatorname{loss}(\mathbf{x}_{i}, \mathbf{y}_{i})=(\mathbf{x}_{i}-\mathbf{y}_{i})^{2} loss(xi,yi)=(xi−yi)2
3.2 代码
a = torch.tensor([1., 2, 3, 4])
b = torch.tensor([4., 5, 6, 7])
loss_fn = nn.MSELoss(reduce=True, size_average=True)
loss = loss_fn(a, b)
print(loss)
#out
tensor(9.)
3.3 说明
两个输入必须要是同一个类型的,当reduce=True返回的是一个标量,当reduce=False返回一个向量;当size_average = True,返回 loss.mean();如果 size_average = False,返回 loss.sum()。默认情况下:两个参数都为True。
4.nn.CrossEntropyLoss
交叉熵:它主要刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近。假设概率分布p为期望输出,概率分布q为实际输出, H ( p , q ) H(p, q) H(p,q)为交叉熵,则
4.1 数学表达式
H ( p , q ) = ∑ x p ( x ) log q ( x ) H(p, q)=\sum_{x} p(x) \log q(x) H(p,q)=x∑p(x)logq(x)
在神经网络中通过Softmax回归将前向传播得到的结果变成概率分布,这是一个常用且有用的方法。
Softmax函数的定义(以第i个节点输出为例):
Softmax ( z i ) = e z i ∑ c = 1 C e z c \operatorname{Softmax}\left(z_{i}\right)=\frac{e^{z_{i}}}{\sum_{c=1}^{C} e^{z_{c}}} Softmax(zi)=∑c=1Cezcezi
其中 z i z_{i} zi为第i个节点的输出值,C为输出节点的个数,即分类的类别个数。通过Softmax函数就可以将多分类的输出值转换为范围在[0, 1]和为1的概率分布。这样就把神经网络的输出也变成了一个概率分布,从而可以通过交叉熵来计算预测的概率分布和真实答案的概率分布之间的距离了。求交叉熵:举个例子,假设N=3,期望输出为p=(1,0,0),实际输出 q 1 q_{1} q1=(0.5,0.4,0.1), q 2 q_{2} q2=(0.8,0.1,0.1) ,那么:
H ( p , q 1 ) = − ( 1 log 0.5 + 0 log 0.4 + 0 log 0.1 + 0 log 0.5 + 1 log 0.6 + 1 log 0.9 ) ) = 0.3 \left.H\left(p, q_{1}\right)=-(1 \log 0.5+0 \log 0.4+0 \log 0.1+0 \log 0.5+1 \log 0.6+1 \log 0.9)\right)=0.3 H(p,q1)=−(1log0.5+0log0.4+0log0.1+0log0.5+1log0.6+1log0.9))=0.3
H ( p , q 2 ) = − ( 1 log 0.8 + 0 log 0.1 + 0 log 0.1 + 0 log 0.2 + 1 log 0.9 + 1 log 0.9 ) ) = 0.19 \left.H\left(p, q_{2}\right)=-(1 \log 0.8+0 \log 0.1+0 \log 0.1+0 \log 0.2+1 \log 0.9+1 \log 0.9)\right)=0.19 H(p,q2)=−(1log0.8+0log0.1+0log0.1+0log0.2+1log0.9+1log0.9))=0.19
通过上面可以看出, q 2 q_{2} q2与p更为接近,它的交叉熵也更小。
为什么要使用交叉熵损失函数呢?
在逻辑回归问题中,常常使用MSE(Mean Squared Error)作为loss函数,此时:
los s = 1 2 m ∑ i m ( y i − y ′ ) 2 \operatorname{los} s=\frac{1}{2 m} \sum_{i}^{m}\left(y_{i}-y^{\prime}\right)^{2} loss=2m1∑im(yi−y′)2
这里的 y i y_{i} yi 就表示期望输出, y ′ y^{\prime} y′ 表示原始的实际输出(就是还没有加softmax)。这里的m表示有 m \mathrm{m} m 个样本, loss为m个样本的loss均值。MSE在逻辑回归问题中比较好用,那么在分类问题中还是如此么? 我们来看看Loss曲线。
将原始的实际输出节点都经过softmax后拿出一个样例来看,使用MSE的loss为的loss函数为:
los s i = ( y i − y i ′ ) 2 = ( y i − e y i ′ ∑ j = 1 n e y i ′ ) 2 \operatorname{los} s_{i}=\left(y_{i}-y^{i^{\prime}}\right)^{2}=\left(y_{i}-\frac{e^{y_{i}^{\prime}}}{\sum_{j=1}^{n} e^{y_{i^{\prime}}}}\right)^{2} lossi=(yi−yi′)2=(yi−∑j=1neyi′eyi′)2
其中 y i y_{i} yi 和 ∑ j = 1 n e y i ′ \sum_{j=1}^{n} e^{y_{i}^{\prime}} ∑j=1neyi′ 为常数,那么loss就可以简化为
loss i = ( c 1 − e y i ′ c 2 ) 2 \operatorname{loss}_{i}=\left(c_{1}-\frac{e^{y i^{\prime}}}{c_{2}}\right)^{2} lossi=(c1−c2eyi′)2
取 c 1 = 1 , c 2 = 2 c_{1}=1, c_{2}=2 c1=1,c2=2, 绘制图像:
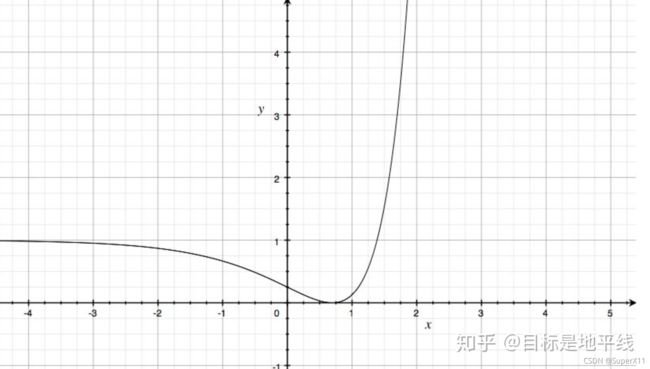
这是一个非凸函数,只有当损失函数为凸函数时,梯度下降算法才能保证达到全局最优解。所以MSE在分类问题中,并不是一个好的loss函数。
如果利用交叉熵作为损失函数的话,那么:
loss = − ∑ i = 1 n y i ∗ log ( y ′ ) \operatorname{loss}=-\sum_{i=1}^{n} y_{i} * \log \left(y_{\prime}\right) loss=−i=1∑nyi∗log(y′)
还是一样, y i y_{i} yi 就表示期望输出, y ′ y^{\prime} y′ 表示原始的实际输出(就是还没有加softmax),由于one-hot 标签的特殊性,一个1,剩下全是0, loss \operatorname{loss} loss 可以简化为:
loss i = − log ( y ′ ) \operatorname{loss}_{i}=-\log \left(y^{\prime}\right) lossi=−log(y′)
加入 (softmax) 得:
loss i = − log ( c 1 − e x c 2 ) \operatorname{loss}_{i}=-\log \left(c_{1}-\frac{e^{x}}{c_{2}}\right) lossi=−log(c1−c2ex)
取 c 1 = 1 , c 2 = 2 c_{1}=1, c_{2}=2 c1=1,c2=2, 绘制图像: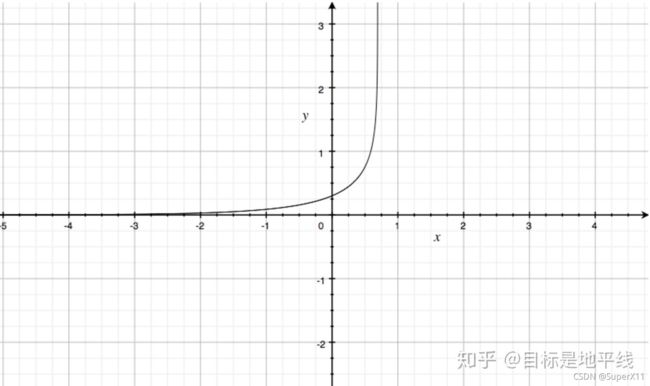
相对MSE而言,曲线整体呈单调性, loss \operatorname{loss} loss 越大,梯度越大。便于梯度下降反向传播,利于优化。所 以一般针对分类问题采用交叉樀作为loss函数。
Pytorch中的CrossEntropyLoss()函数,计算公式如下:
loss ( x , class ) = − log ( exp ( x [ class ] ) ∑ j exp ( x [ j ] ) ) = − x [ class ] + log ( ∑ j exp ( x [ j ] ) ) \operatorname{loss}(x, \text { class })=-\log \left(\frac{\exp (x[\text { class }])}{\sum_{j} \exp (x[j])}\right)=-x[\text { class }]+\log \left(\sum_{j} \exp (x[j])\right) loss(x, class )=−log(∑jexp(x[j])exp(x[ class ]))=−x[ class ]+log(j∑exp(x[j]))
4.2 代码
entroy = nn.CrossEntropyLoss()
input = torch.Tensor([[-0.7715, -0.6205, -0.2562]])
target = torch.tensor([0])
output = entroy(input, target)
print(output)
#output
tensor(1.3447)
4.3 说明
按公式计算如下:
−x[0]+log(exp(x[0])+exp(x[1])+exp(x[2]))=0.7715+log(exp(−0.7715)+exp(−0.6205)+exp(−0.2562)=1.3447266007601868=0.7715+log(exp(-0.7715)+exp(-0.6205)+exp(-0.2562)=1.3447266007601868=0.7715+log(exp(−0.7715)+exp(−0.6205)+exp(−0.2562)=1.3447