GCN原理的直观解释
本文为学习笔记,整理了自己对GCN的直观理解帮助记忆,不涉及过多数学知识,若有错误和理解不到位的地方请原谅和指正。
GCN的核心公式
f ( H ( l ) , A ) = σ ( D ^ − 1 2 A ^ D ^ − 1 2 H ( l ) W ( l ) ) f(H^{(l)}, A) = \sigma\left( \hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}H^{(l)}W^{(l)}\right) f(H(l),A)=σ(D^−21A^D^−21H(l)W(l))
其中, A A A为邻接矩阵, A ^ = A + I \hat{A}=A+I A^=A+I, D D D为度矩阵, H ( l ) H^{(l)} H(l)为输入特征,即节点的特征表示, W ( l ) W^{(l)} W(l)为网络参数, σ ( ⋅ ) \sigma(·) σ(⋅)为激活函数, f ( H ( l ) , A ) f(H^{(l)}, A) f(H(l),A)为本层输出,在多层GCN中也为下一层的输入,即 H ( l + 1 ) H^{(l+1)} H(l+1)。
为了更直观地理解GCN的公式,先举一个最简单的版本,再递进地理解GCN的核心思想。
f ( H ( l ) , A ) = σ ( A H ( l ) W ( l ) ) f(H^{(l)}, A) = \sigma\left( AH^{(l)}W^{(l)}\right) f(H(l),A)=σ(AH(l)W(l))
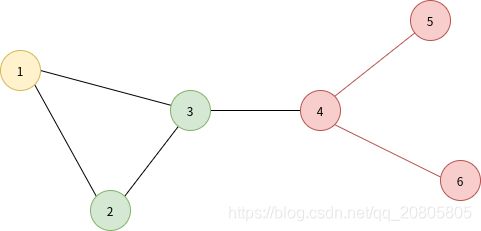
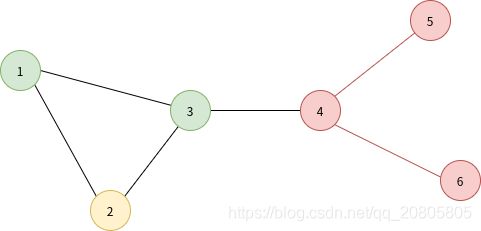
引入一个简单的无向图辅助分析。

可获得其邻接矩阵
A = [ 0 1 1 0 0 0 1 0 1 0 0 0 1 1 0 1 0 0 0 0 1 0 1 1 0 0 0 1 0 0 0 0 0 1 0 0 ] A =\begin{bmatrix} 0 & 1 & 1&0&0&0 \\ 1 & 0&1&0&0&0\\1&1&0&1&0&0\\0 &0&1&0&1&1\\0&0&0&1&0&0\\0&0&0&1&0&0 \end{bmatrix} A=⎣⎢⎢⎢⎢⎢⎢⎡011000101000110100001011000100000100⎦⎥⎥⎥⎥⎥⎥⎤
假设特征矩阵为 H H H,行向量为对应索引节点的特征。
H = [ 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 5 5 5 5 5 5 6 6 6 6 6 6 ] H = \begin{bmatrix} 1 & 1 & 1&1&1&1 \\ 2 & 2&2&2&2&2\\3&3&3&3&3&3\\4 &4&4&4&4&4\\5&5&5&5&5&5\\6&6&6&6&6&6 \end{bmatrix} H=⎣⎢⎢⎢⎢⎢⎢⎡123456123456123456123456123456123456⎦⎥⎥⎥⎥⎥⎥⎤
计算 A H AH AH实际上就是将每个节点邻接的节点特征相加,作为该节点新的特征表示,如果不好理解可以看下方图例。
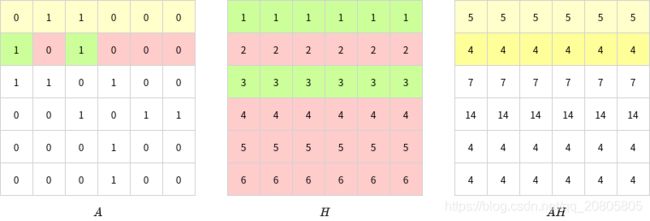
其他节点同理。如果熟悉卷积网络,就可以看出上述操作实际上是使用了一个全1的卷积核,对邻居节点进行了一次卷积操作 ,从而将邻居节点的信息聚集到了中心节点上。
由此引申出两个问题:
- 在简单版本中,只将邻居节点的特征相加得到节点的新特征表示,而没有考虑到节点自身的特征。在一些研究工作中,节点的初始特征往往是经由预训练模型(如bert)或算法得到的,包含丰富的信息,不能直接忽略。
- 由于是新节点特征是简单相加得到,因此拥有较多邻居的节点特征会迅速增大,而邻居较少的节点特征变化不明显,从上图中 A H AH AH节点4的特征变化情况可以看出。容易导致梯度过大,对模型训练产生不利影响。
对第一个问题,GCN对给邻接矩阵加上一个单位矩阵,即 A ^ = A + I \hat{A}=A+I A^=A+I,令节点形成自环,在卷积操作时,会加上节点自身特征。针对第二个问题,GCN对矩阵 A ^ \hat{A} A^进行归一化。
邻接矩阵的对称归一化
再写一遍GCN核心公式
f ( H ( l ) , A ) = σ ( D ^ − 1 2 A ^ D ^ − 1 2 H ( l ) W ( l ) ) f(H^{(l)}, A) = \sigma\left( \hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}H^{(l)}W^{(l)}\right) f(H(l),A)=σ(D^−21A^D^−21H(l)W(l))
GCN采用对称归一化方法,实践中可采用上式的 D ^ − 1 2 A ^ D ^ − 1 2 \hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}} D^−21A^D^−21部分,会将原本的 A ^ \hat{A} A^进行归一化,避免梯度爆炸的发生,也一定程度上提升了相对重要的节点所占的权重。 D ^ \hat{D} D^为 A ^ \hat{A} A^的度矩阵,注意包含自环。
D ^ = [ 3 0 0 0 0 0 0 3 0 0 0 0 0 0 4 0 0 0 0 0 0 4 0 0 0 0 0 0 2 0 0 0 0 0 0 2 ] \hat{D}= \begin{bmatrix} 3 & 0 & 0&0&0&0 \\ 0 & 3&0&0&0&0\\0&0&4&0&0&0\\0 &0&0&4&0&0\\0&0&0&0&2&0\\0&0&0&0&0&2 \end{bmatrix} D^=⎣⎢⎢⎢⎢⎢⎢⎡300000030000004000000400000020000002⎦⎥⎥⎥⎥⎥⎥⎤
'''code'''
A = torch.FloatTensor([
[1,1,1,0,0,0],
[1,1,1,0,0,0],
[1,1,1,1,0,0],
[0,0,1,1,1,1],
[0,0,0,1,1,0],
[0,0,0,1,0,1]])
D = []
for i in A:
D.append(sum(i))
D = torch.tensor(D)
D = D.pow(-0.5)
# 使用按位乘法简化矩阵乘法
DA= torch.mul(A,D.view(-1,1))
DAD= torch.mul(DA,D.view(1,-1))
'''output'''
DAD=
tensor([
[0.3333, 0.3333, 0.2887, 0.0000, 0.0000, 0.0000],
[0.3333, 0.3333, 0.2887, 0.0000, 0.0000, 0.0000],
[0.2887, 0.2887, 0.2500, 0.2500, 0.0000, 0.0000],
[0.0000, 0.0000, 0.2500, 0.2500, 0.3536, 0.3536],
[0.0000, 0.0000, 0.0000, 0.3536, 0.5000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.3536, 0.0000, 0.5000]])
假设归一化后的邻接矩阵为 A ~ \tilde{A} A~,可得每位的计算公式为
A ~ i , j = D ^ i − 1 2 ∗ A ^ i , j ∗ D ^ j − 1 2 \tilde{A}_{i,j}=\hat{D}^{-\frac{1}{2}}_{i}* \hat{A}_{i,j}* \hat{D}^{-\frac{1}{2}}_j A~i,j=D^i−21∗A^i,j∗D^j−21
再与特征矩阵相乘,每个节点聚合后的新特征表示为相邻节点特征的加权求和
H ^ i = ∑ j = 1 N A ~ i , j ∗ H j \hat{H}_i=\sum_{j=1}^N\tilde{A}_{i,j}*H_j H^i=j=1∑NA~i,j∗Hj
因此可将核心公式简化为
f ( H ( l ) , A ) = σ ( H ^ ( l ) W ( l ) ) f(H^{(l)}, A) = \sigma\left( \hat{H}^{(l)}W^{(l)}\right) f(H(l),A)=σ(H^(l)W(l))
即,将聚合后特征输入到一个参数为 W ( l ) W^{(l)} W(l)的全连接层,再通过激活函数 σ ( ⋅ ) \sigma(·) σ(⋅),输出节点特征,是一层非常简单的神经网络。
参考
GCN作者自己的讲解(推荐阅读)
对称归一化的原理解释