pytorch小知识点(三)-------Tensor的indices操作
一、Tesnor
先简单介绍一下Tensor。Tensor是pytorch的核心,它是一个包含单一数据类型的多维矩阵。
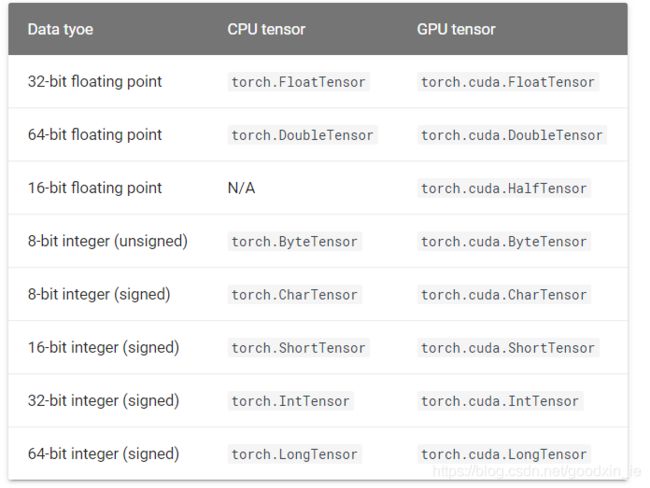
pyTorch定义了七种CPU tensor类型和八种GPU tensor类型:
默认的torch.Tensor是FloatTensor。我们可以简单地向下面的方式创建一个Tensor:
"""
FloatTensor
"""
x1 = torch.FloatTensor([1,2,3,4,5,6])
x1
Out[100]: tensor([1., 2., 3., 4., 5., 6.])
x1.dtype
Out[115]: torch.float32
"""
LongTensor
"""
x2 = torch.LongTensor([1,2,3,4,5,6])
x2
Out[116]: tensor([1, 2, 3, 4, 5, 6])
x2.dtype
Out[117]: torch.int64二、Tensor的indices操作
我们都知道对于Tesnor可以向numpy一样进行slice(切片)操作,如下:
x = torch.randn((3,4))
x
Out[119]:
tensor([[-0.2558, 0.9740, -0.4165, 0.0370],
[-0.6938, -0.6043, -0.1243, -1.0082],
[ 0.4293, 1.1933, 0.6975, 0.1752]])
x[1,:] #取第二行
Out[120]: tensor([-0.6938, -0.6043, -0.1243, -1.0082])
x[:,2] #取第三列
Out[121]: tensor([-0.4165, -0.1243, 0.6975])但是Tensor中有一个独特的indices操作,按照我们给的索引进行取数:
形式为x[mask]
- x要求为1个Tensor
- mask必须为ByteTensor或者LongTensor(注意:这种格式的mask对应的结果是完全不同的)
1.当mask为ByteTensor时,要求mask必须和x形状相同。
此时mask表示是否保留x中对应位置的数。若mask中对应位不为0,则保留x中对应数。最终返回值是一个1-D Tensor,长度等于mask中非0元素的个数(因此,建议大家在mask中只用0和1两种数字就可以了)
e.g
x = torch.Tensor([[0,1,2,3,4],[5,6,7,8,9],[10,11,12,13,14]])
"""
mask1 对应保留x中的奇数
"""
mask1 = torch.ByteTensor([[0,1,0,1,0],[0,1,0,1,0],[0,1,0,1,0]])
"""
mask2 对应保留x中的偶数
"""
mask2 = torch.ByteTensor([[1,0,1,0,1],[1,0,1,0,1],[1,0,1,0,1]])
x[mask1]
Out[148]: tensor([ 1., 3., 6., 8., 11., 13.])
x[mask2]
Out[149]: tensor([ 0., 2., 4., 5., 7., 9., 10., 12., 14.])
"""
mask3 只是为了证明mask中所有非0数均起相同作用,此时mask1和mask3的实质作用相同
但是不推荐使用mask3这种存在0和1之外其他数的形式,mask1表达的意义明显比mask3清晰
"""
mask3 = torch.ByteTensor([[0,1,0,3,0],[0,6,0,8,0],[0,11,0,13,0]])
x[mask3]
Out[151]: tensor([ 1., 3., 6., 8., 11., 13.])2.当mask为LongTensor时,此时x和mask形状不必相同。
注:当mask为LongTensor时,如果不熟悉的话最好使用1-D Tensor的mask
我们先看看x为1-D,mask为1-D Tensor的情况
x1 = torch.Tensor([0,1,2,3,4])
mask1 = torch.LongTensor([1,0,2])
x1[mask1]
Out[174]: tensor([1., 0., 2.])
"""
为什么输出会是[1,0,2]???
"""
mask2 = torch.LongTensor([4,3,2,1,0])
x1[mask2]
Out[176]: tensor([4., 3., 2., 1., 0.])
"""
到这儿我们该看懂了吧,mask为LongTensor时,x[mask]相当于一个在0纬度上的gather操作
就是按照mask中的索引对应的x中的数字放到索引当前位置,用mask1来举例,mask1中第一个数为1,我们就在结果的第一个数上放x1[1],mask1中第二个数为0,结果的第二个数就是x1[0]
因此,mask1对应的输出就是[x1[mask1[0],x1[mask1[1],x1[mask1[2]]
此时不难理解mask2对应的输出为[4., 3., 2., 1., 0.]了吧
"""那么x为2-D,mask为1-D的情况呢?
x2 = torch.Tensor([[ 0., 1., 2., 3., 4.],
[ 5., 6., 7., 8., 9.],
[10., 11., 12., 13., 14.]])
mask1 = torch.LongTensor([0,1,2])
x2[mask1]
Out[182]:
tensor([[ 0., 1., 2., 3., 4.],
[ 5., 6., 7., 8., 9.],
[10., 11., 12., 13., 14.]])
mask2 = torch.LongTensor([0,2,1])
x2[mask2]
Out[184]:
tensor([[ 0., 1., 2., 3., 4.],
[10., 11., 12., 13., 14.],
[ 5., 6., 7., 8., 9.]])
"""
此时我们可以得出结论,不论x是几维的,mask为LongTensor时都是按照mask中的顺序排列x[mask[i]]
上面的mask1对应的结果应该是 [x2[0],x2[1],x2[2]]
mask2对应的结果是[x2[0],x2[1],x2[2]]
直白来说这种操作就是对x中的第一个维度上的重排列
"""有了上面的铺垫,我们可以看一下当mask为多维时的情况
x2 = torch.Tensor([[ 0., 1., 2., 3., 4.],
[ 5., 6., 7., 8., 9.],
[10., 11., 12., 13., 14.]])
mask1 = torch.LongTensor([[0,1,2],[0,1,2]])
x2[mask1]
Out[188]:
tensor([[[ 0., 1., 2., 3., 4.],
[ 5., 6., 7., 8., 9.],
[10., 11., 12., 13., 14.]],
[[ 0., 1., 2., 3., 4.],
[ 5., 6., 7., 8., 9.],
[10., 11., 12., 13., 14.]]])
mask2 = torch.LongTensor([[0,0,0],[0,0,0]])
x2[mask2]
Out[190]:
tensor([[[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.]],
[[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.],
[0., 1., 2., 3., 4.]]])
"""
what?什么情况,输出怎么变得这么复杂?冷静下来仔细分析一下,
x2[mask1]看起来是将x2在一个新的维度上扩展了两倍 ,x2[mask2]好像是将x2[0]先复制三遍,再在一个新的维度上扩展了两倍
貌似有点规律。我们还记得上上面的结论吗,mask为LongTensor时就是将x[mask[i]]按照mask中的顺序排列
我们试着将mask1和mask2中的数字i替换成x2[i]看看是不是就是输出结果呢?
其实,不论mask多么复杂,我们将mask中的数字i当作x在第一个纬度上的索引就好了,然后将i在原位置替换成x[i]就是最终的输出结果了
"""
"""
我们来测试一下上面的结论
x 为1-D mask为 2-D
"""
x3 = torch.Tensor([0.1,0.2,0.3])
mask1 = torch.LongTensor([[0,1,2],[0,1,2]])
x3[mask1]
Out[193]:
tensor([[0.1000, 0.2000, 0.3000],
[0.1000, 0.2000, 0.3000]])
mask2 = torch.LongTensor([[0,0,0],[0,0,0]])
x3[mask2]
Out[194]:
tensor([[0.1000, 0.1000, 0.1000],
[0.1000, 0.1000, 0.1000]])
x[mask]中mask为LongTensor时与gather操作的不同
x[mask]中的mask始终指代的是x的第一个维度上的索引。
gather中的index可以为指定dim上的索引,而且对于gather操作来说,index必须和操作数shape相同
三、indices为ByteTensor的应用实例
这个实例完成的功能是在一个2-D Tensor中截取每一行最大的前ni(每一行的nibuxiangdeng)个数
我们有一个4*5的Tensor
x = torch.randn((4,5))
x
Out[199]:
tensor([[ 1.8299, 0.0714, -0.1213, -0.5910, -0.2492],
[-1.5000, -0.5365, 0.1588, 1.1101, 0.8724],
[ 1.1998, 2.3945, 1.0767, 0.5229, 0.3283],
[-1.0195, 0.3819, -1.0285, 1.2028, -1.0717]])我们来截取他每行的前[1,2,3,4]个数,即取第一行最大的1个数,第二行2个...
x = torch.randn((4,5))
"""
x
Out[199]:
tensor([[ 1.8299, 0.0714, -0.1213, -0.5910, -0.2492],
[-1.5000, -0.5365, 0.1588, 1.1101, 0.8724],
[ 1.1998, 2.3945, 1.0767, 0.5229, 0.3283],
[-1.0195, 0.3819, -1.0285, 1.2028, -1.0717]])
"""
_,indices = x.sort(dim=1,descending=True)
"""
indices
Out[201]:
tensor([[0, 1, 2, 4, 3],
[3, 4, 2, 1, 0],
[1, 0, 2, 3, 4],
[3, 1, 0, 2, 4]])
"""
_,idx = indices.sort(dim=1)
"""
idx
Out[203]:
tensor([[0, 1, 2, 4, 3],
[4, 3, 2, 0, 1],
[1, 0, 2, 3, 4],
[2, 1, 3, 0, 4]])
"""
num = torch.LongTensor([[1],[2],[3],[4]])
"""
num
Out[205]:
tensor([[1],
[2],
[3],
[4]])
"""
num = num.expand_as(idx)
"""
num
Out[207]:
tensor([[1, 1, 1, 1, 1],
[2, 2, 2, 2, 2],
[3, 3, 3, 3, 3],
[4, 4, 4, 4, 4]])
"""
mask = idx上面例子中的前面的两次排序操作都是为了获得最终的mask,最终的mask为1的地方就是x中最大的几个数(每行的前ni个)。
上面例子还有一个重要的知识点,就是对一个2-D Tensor使用两次sort函数(对原矩阵、第一次sort之后的index)后,index(第二个变量)的输出是原矩阵一个由大到小(或由小到大)的映射,映射的值为整数,位置保持不变。
我们可以用个例子体会一下:
x
Out[215]:
tensor([[ 0.2849, -1.0989, -0.2956, 1.2607, -1.1120],
[ 0.0420, 0.3557, -0.7565, 0.5844, -2.0583],
[ 0.6427, -1.5065, 0.9481, -1.2509, 2.2974],
[ 0.1249, -1.1839, -0.3964, 0.3081, -0.3041]])
_,indices = x.sort(dim=1)
_,idx = indices.sort(dim=1)
idx
Out[218]:
tensor([[3, 1, 2, 4, 0],
[2, 3, 1, 4, 0],
[2, 0, 3, 1, 4],
[3, 0, 1, 4, 2]])参考资料:[1]找出矩阵中升序或降序元素的位置