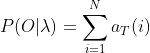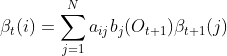【统计学习方法】EM算法实现之隐马尔科夫模型HMM
1 基本概念
1.1 马尔科夫链（维基百科）
马尔可夫链（英语：Markov chain），又称离散时间马尔可夫链（discrete-time Markov chain，缩写为DTMC），因俄国数学家安德烈·马尔可夫得名，为状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备“无记忆”的性质：下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性”称作马尔可夫性质。
1.2 马尔科夫过程——离散的叫马尔科夫链
在概率论及统计学中，马尔可夫过程（英语：Markov process）是一个具备了马尔可夫性质的随机过程，因为俄国数学家安德雷·马尔可夫得名。马尔可夫过程是不具备记忆特质的（memorylessness）。换言之，马尔可夫过程的条件概率仅仅与系统的当前状态相关，而与它的过去历史或未来状态，都是独立、不相关的。
具备离散状态的马尔可夫过程，通常被称为马尔可夫链。马尔可夫链通常使用离散的时间集合定义，又称离散时间马尔可夫链。有些学者虽然采用这个术语，但允许时间可以取连续的值。
1.3 隐马尔科夫模型定义
隐马尔可夫模型（Hidden Markov Model；缩写：HMM）或称作隐性马尔可夫模型，是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，例如模式识别。
在正常的马尔可夫模型中，状态对于观察者来说是直接可见的。这样状态的转换概率便是全部的参数。而在隐马尔可夫模型中，状态并不是直接可见的，但受状态影响的某些变量则是可见的。每一个状态在可能输出的符号上都有一概率分布。因此输出符号的序列能够透露出状态序列的一些信息。
隐马尔科夫模型是关于时序的概率模型，描述一个由隐藏的马尔科夫链随机生成不可观测的状态随机序列，再由各个状态生成一个可观测的观测随机序列的过程。
1.4 隐马尔科夫模型参数的确定
1.4.1 初始概率分布
可能是状态1，状态2 ... 状态n，于是就有个N点分布：
|
状态1 | 状态2 | ... | 状态n |
| 概率 |  |
 |
.. |  |
即：对应个n维的向量。
上面这个n维的向量就是初始概率分布，记做π。
1.4.2 状态转移矩阵A
因为
和不独立，所以是状态1的概率有：是状态1时是状态1，是状态2时是状态1,..., 是状态n时是状态1，如下表
| \ |
状态1 | 状态2 | ... | 状态n |
| 状态1 | P11 | P12 | ... | P1n |
| 状态2 | P21 | P22 | ... | P2n |
| ... | ... | ... | ... | ... |
| 状态n | Pn1 | Pn2 | ... | Pnn |
即：->对应n*n的矩阵。
同理：
-> 
对应个n*n的矩阵。
上面这些n*n的矩阵被称为状态转移矩阵，用An*n表示。
当然了，真要说的话， -> 的状态转移矩阵一定都不一样，但在实际应用中一般将这些状态转移矩阵定为同一个，即：只有一个状态转移矩阵。
1.4.3 观测矩阵B
如果对于有：状态1, 状态2, ..., 状态n，那的每一个状态都会从下面的m个观测中产生一个：观测1, 观测2, ..., 观测m，所以有如下矩阵：
\ |
观测1 | 观测2 | ... | 观测m |
| 状态1 | P11 | P12 | ... | P1m |
| 状态2 | P21 | P22 | ... | P2m |
| ... | ... | ... | ... | ... |
| 状态n | Pn1 | Pn2 | ... | Pnm |
这可以用一个n*m的矩阵表示，也就是观测矩阵，记做Bn*m。
由于HMM用上面的π，A，B就可以描述了，于是我们就可以说：HMM由初始概率分布π、状态转移概率分布A以及观测概率分布B确定，为了方便表达，把A, B, π 用 λ 表示，即：
λ = (A, B, π)
2 隐马尔科夫模型
隐马尔科夫模型是一个生成模型，也就意味着一旦掌握了其底层结构，就可以产生数据。
HMM模型一共有三个经典的问题需要解决：
1） 评估观察序列概率。即给定模型
和观测序列
，计算在模型λ下观测序列出现的概率
。这个问题的求解需要用到前向后向算法，我们在这个系列的第二篇会详细讲解。这个问题是HMM模型三个问题中最简单的。
2）模型参数学习问题。即给定观测序列，估计模型的参数，使该模型下观测序列的条件概率最大。这个问题的求解需要用到基于EM算法的鲍姆-韦尔奇算法， 我们在这个系列的第三篇会详细讲解。这个问题是HMM模型三个问题中最复杂的。
3）预测问题，也称为解码问题。即给定模型和观测序列，求对给定观测序列条件概率
最大的状态序列 
。即给定观测序列条件下，最可能出现的对应的状态序列，这个问题的求解需要用到基于动态规划的维特比算法，我们在这个系列的第四篇会详细讲解。这个问题是HMM模型三个问题中复杂度居中的算法。
2.1 概率计算问题
穷举算法，有N中状态，经过T时间，则有
种可能(因为每一种状态都可能观测到
)，计算量巨大。但是很多路径是重复，基于动态规划的知识，我们可以重复利用很多节点的计算结果，所以出来了前向算法和后向算法。
2.1.1 前向概率
给定隐马尔可夫模型，定义到时刻t为止的观测序列为，且状态为
的概率为前向概率，记作：
可以递推地求得前向概率
及观测序列概率。
定义解析：由于每个状态生成一个观测变量，那么在t时刻就会生成t个观测变量，在t时刻处于状态i的概率就是前向概率。
2.1.1 前向算法
算法的目的：根据初始参数和观测序列求出观测序列概率
前向概率的定义是：当第t个时刻的状态为i时，前面的时刻分别观测到
的概率，即：
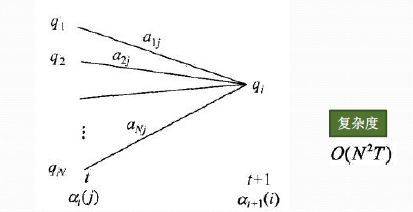
从上图可以看出，我们可以基于时刻t时各个隐藏状态的前向概率，再乘以对应的状态转移概率，即
就是在时刻t观测到，并且时刻t隐藏状态
, 时刻t+1隐藏状态
的概率。如果将像上面所有的线对应的概率求和，即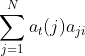
就是在时刻t观测到，并且时刻t+1隐藏状态的概率。继续一步，由于观测状态
只依赖于t+1时刻隐藏状态, 这样![\left [ \sum_{j=1}^{N}a_t(j)a_{ji} \right ]b_i(O_{t+1})](http://img.e-com-net.com/image/info8/68cb52a1a98247c59c248dd2efe7c96f.gif)
就是在在时刻t+1观测到
，并且时刻t+1隐藏状态的概率。而这个概率，恰恰就是时刻t+1对应的隐藏状态i的前向概率，这样我们得到了前向概率的递推关系式如下：
![a_{t+1}(i) = \left [ \sum_{j=1}^{N} a_t(j)a_{ji}\right ]b_i(o_{t+1})](http://img.e-com-net.com/image/info8/08982e67f628452c8936656d7dca68f8.gif)
前向算法步骤：
输入：HMM模型，观测序列
输出：观测序列概率(|)
1) 计算时刻1的各个隐藏状态前向概率：
2) 递推时刻2,3,...2,3,...T时刻的前向概率：
![a_{t+1}(i) = \left [ \sum_{j=1}^{N} a_t(j)a_{ji} \right ]b_i(o_{t+1}),i=1,2...N](http://img.e-com-net.com/image/info8/24805cb9add84352af440acc6ab4d618.gif)
3) 计算最终结果：
PS：这里的 
中i表示第i号状态，t表示第t时刻。有的教程中会把i和t位置调换一下，变成 ，其实都一样。
代码实现：
def forward(obs_seq):
"""前向算法"""
N = A.shape[0]
T = len(obs_seq)
# F保存前向概率矩阵
F = np.zeros((N,T))
F[:,0] = pi * B[:, obs_seq[0]] # 初始状态输出序列元素0概率
for t in range(1, T):
for n in range(N):
# t时刻各个状态，是t-1时刻各个状态转移过来的
# A[:,n]表示各个状态转移到状态n
# F[:,t-1]表示从初始时刻到t-1处于该状态的概率（不准确的理解）
# B[n, obs_seq[t]]表示n状态输出obs_seq[t]观察值的概率
# 利用点乘 累加 所有状态
F[n,t] = np.dot(F[:,t-1], (A[:,n])) * B[n, obs_seq[t]]
return F
2.1.2 后向算法
后向算法和前向算法非常类似，都是用的动态规划，唯一的区别是选择的局部状态不同，后向算法用的是“后向概率”。
后向概率的定义是：当第t个时刻的状态为i时，后面的时刻分别观测到
的概率，即：
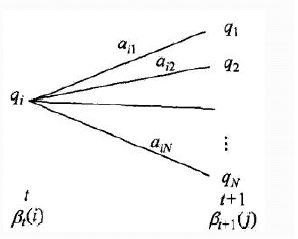
后向概率的动态规划递推公式和前向概率是相反的。现在我们假设我们已经找到了在时刻t+1时各个隐藏状态的后向概率
，现在我们需要递推出时刻t时各个隐藏状态的后向概率。如下图，我们可以计算出观测状态的序列为， t时隐藏状态, 时刻t+1隐藏状态为的概率为
, 接着可以得到观测状态的序列为， t时隐藏状态为, 时刻t+1隐藏状态为的概率为
, 则把下面所有线对应的概率加起来，我们可以得到观测状态的序列为， t时隐藏状态为的概率为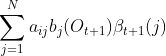
，这个概率即为时刻t的后向概率。
这样我们得到了后向概率的递推关系式如下：
后向算法步骤：
代码实现：
def backward(obs_seq):
"""后向算法"""
N = A.shape[0]
T = len(obs_seq)
# X保存后向概率矩阵
X = np.zeros((N,T))
#t=T，T+1已经不观察了，后向概率都为1
X[:,-1:] = 1
for t in reversed(range(T-1)):
for n in range(N):
#t时刻转移概率*(t+1)时刻的后向概率
X[n,t] = np.sum(X[:,t+1] * A[n,:] * B[:, obs_seq[t+1]])
return X
2.3 学习问题
Baum-Welch算法也就是EM算法，己知观测序列,估计模型参数，使得在该模型下观测序列概率最大。即用极大似然估计的方法估计参数。
2.4 预测问题（viterbi算法）
参考视频：https://www.youtube.com/watch?v=RKDIpPyeTTk
参考文章：https://www.zhihu.com/question/20136144
删掉了不可能是答案的路径，就是viterbi算法（维特比算法）的重点，因为后面我们再也不用考虑这些被删掉的路径了
代码实现：
def viterbi(self, obs_seq):
"""
Returns
-------
V : numpy.ndarray
V [s][t] = Maximum probability of an observation sequence ending
at time 't' with final state 's'
观察序列
prev : numpy.ndarray
Contains a pointer to the previous state at t-1 that maximizes
V[state][t]
"""
N = self.A.shape[0]
T = len(obs_seq)
prev = np.zeros((T - 1, N), dtype=int)
# DP matrix containing max likelihood of state at a given time
# 隐状态个数, 观测序列长度
V = np.zeros((N, T))
# 0时刻观测状态 = 状态初始概率 * 每个状态输出观测概率
V[:,0] = self.pi * self.B[:,obs_seq[0]]
for t in range(1, T):
for n in range(N):
# 上一时刻状态概率 * 状态转移概率(每一个状态转移到状态n) * 观察概率
seq_probs = V[:,t-1] * self.A[:,n] * self.B[n, obs_seq[t]]
# prev用于记录最大概率是从哪个状态转移过来的 -- >记录转移路径
prev[t-1,n] = np.argmax(seq_probs)
# 这里找出概率当前状态最大的概率,实质就是删除不可能的路径 --> 记录最大概率
V[n,t] = np.max(seq_probs)
return V, prev
3 代码实现
完整实现
import numpy as np
class HMM:
"""
Order 1 Hidden Markov Model
Attributes
----------
A : numpy.ndarray
State transition probability matrix
B: numpy.ndarray
Output emission probability matrix with shape(N, number of output types)
pi: numpy.ndarray
Initial state probablity vector
Common Variables
----------------
obs_seq : list of int
list of observations (represented as ints corresponding to output
indexes in B) in order of appearance
T : int
number of observations in an observation sequence
N : int
number of states
"""
def __init__(self, A, B, pi):
self.A = A
self.B = B
self.pi = pi
def _forward(self, obs_seq):
N = self.A.shape[0]
T = len(obs_seq)
F = np.zeros((N,T))
F[:,0] = self.pi * self.B[:, obs_seq[0]]
for t in range(1, T):
for n in range(N):
F[n,t] = np.dot(F[:,t-1], (self.A[:,n])) * self.B[n, obs_seq[t]]
return F
def _backward(self, obs_seq):
N = self.A.shape[0]
T = len(obs_seq)
X = np.zeros((N,T))
X[:,-1:] = 1
for t in reversed(range(T-1)):
for n in range(N):
X[n,t] = np.sum(X[:,t+1] * self.A[n,:] * self.B[:, obs_seq[t+1]])
return X
def observation_prob(self, obs_seq):
""" P( entire observation sequence | A, B, pi ) """
return np.sum(self._forward(obs_seq)[:,-1])
def state_path(self, obs_seq):
"""
Returns
-------
V[last_state, -1] : float
Probability of the optimal state path
path : list(int)
Optimal state path for the observation sequence
"""
V, prev = self.viterbi(obs_seq)
# Build state path with greatest probability
last_state = np.argmax(V[:,-1])
path = list(self.build_viterbi_path(prev, last_state))
return V[last_state,-1], reversed(path)
def viterbi(self, obs_seq):
"""
Returns
-------
V : numpy.ndarray
V [s][t] = Maximum probability of an observation sequence ending
at time 't' with final state 's'
prev : numpy.ndarray
Contains a pointer to the previous state at t-1 that maximizes
V[state][t]
"""
N = self.A.shape[0]
T = len(obs_seq)
prev = np.zeros((T - 1, N), dtype=int)
# DP matrix containing max likelihood of state at a given time
V = np.zeros((N, T))
V[:,0] = self.pi * self.B[:,obs_seq[0]]
for t in range(1, T):
for n in range(N):
seq_probs = V[:,t-1] * self.A[:,n] * self.B[n, obs_seq[t]]
prev[t-1,n] = np.argmax(seq_probs)
V[n,t] = np.max(seq_probs)
return V, prev
def build_viterbi_path(self, prev, last_state):
"""Returns a state path ending in last_state in reverse order."""
T = len(prev)
yield(last_state)
for i in range(T-1, -1, -1):
yield(prev[i, last_state])
last_state = prev[i, last_state]
def baum_welch_train(self, obs_seq):
N = self.A.shape[0]
T = len(obs_seq)
forw = self._forward(obs_seq)
back = self._backward(obs_seq)
# P( entire observation sequence | A, B, pi )
obs_prob = np.sum(forw[:,-1])
if obs_prob <= 0:
raise ValueError("P(O | lambda) = 0. Cannot optimize!")
xi = np.zeros((T-1, N, N))
for t in range(xi.shape[0]):
xi[t,:,:] = self.A * forw[:,[t]] * self.B[:,obs_seq[t+1]] * back[:, t+1] / obs_prob
gamma = forw * back / obs_prob
# Gamma sum excluding last column
gamma_sum_A = np.sum(gamma[:,:-1], axis=1, keepdims=True)
# Vector of binary values indicating whether a row in gamma_sum is 0.
# If a gamma_sum row is 0, save old rows on update
rows_to_keep_A = (gamma_sum_A == 0)
# Convert all 0s to 1s to avoid division by zero
gamma_sum_A[gamma_sum_A == 0] = 1.
next_A = np.sum(xi, axis=0) / gamma_sum_A
gamma_sum_B = np.sum(gamma, axis=1, keepdims=True)
rows_to_keep_B = (gamma_sum_B == 0)
gamma_sum_B[gamma_sum_B == 0] = 1.
obs_mat = np.zeros((T, self.B.shape[1]))
obs_mat[range(T),obs_seq] = 1
next_B = np.dot(gamma, obs_mat) / gamma_sum_B
# Update model
self.A = self.A * rows_to_keep_A + next_A
self.B = self.B * rows_to_keep_B + next_B
self.pi = gamma[:,0] / np.sum(gamma[:,0])
参考：
隐马尔可夫(HMM)、前/后向算法、Viterbi算法
【火炉炼AI】机器学习044-创建隐马尔科夫模型
隐马尔可夫模型HMM及Python实现
隐马尔可夫模型之Baum-Welch算法详解
HMM超详细讲解+代码