吃瓜教程|Task1(概览西瓜书第1、2章)
前言
之前有概述性的看过西瓜书,但中间看到很多不会的内容都会选择性的跳过。这次借Datawhale组队学习的机会再温习一遍西瓜书,争取把基础打牢固一些,方便后面理论方面可以更进一步的推进。当然顺便也练习自己写博客的能力。
概述
机器学习常分为两类
监督学习:分类、回归
无监督学习:聚类
归纳偏好(inductive bias):维基百科
机器学习算法在学习过程中对某种类型假设的偏好,称为“归纳偏好”
“没有免费的午餐”定理(No Free Lunch Theorem, NFL):维基百科
当任何两种优化算法的性能在所有可能的问题上取平均值时,它们都是等效的。但这有一个重要前提,所有问题出现的机会相同(或者说所有问题同等重要)。因此,NFL定理体现的寓意是,空谈哪种“学习算法”更好毫无意义,要讨论算法的相对优劣,必须针对具体的学习问题,学习算法自身的归纳偏好与问题是否匹配,往往会起到决定性的作用。
模型评估与选择
错误率:分类错误的样本数占总数的比例,E = a/m
精度:1 - a/m
误差:学习器的实际预测输出与样本的真实输出之间的差异
训练误差(经验误差,training error,empirical error):学习器在训练集上的误差
泛化误差(generalization error):学习器在新样本上的误差
过拟合:学习器把训练样本学得“太好”了,很可能已经把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质,这样导致泛化性能下降。
欠拟合:学习器对样本的特征没有学习充分,学习能力低下。
评估方法
留出法
将数据集D划分为两个互斥的集合,其中一个集合作为训练集S,另一个作为测试集T。在S上训练出模型后,用T来评估其测试误差,作为对泛化误差的估计。
注意点
1.训练/测试集需要保证数据分布的一致性,在训练集、测试集划分时,需要保证类别比例相同(分层抽样),防止学习器对类别偏差进行学习。
2.在对训练集和测试集的划分中,可能存在样本顺序/选择不同产生的偏差,这时产生的结果往往不够稳定可靠,可以在使用留出法时采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。
3.另外一个问题是:弱令训练集S包含绝大多数样本,则训练出来的模型可能更接近于用D训练出的模型,但由于T比较小,评估结果可能不够稳定准确;若令测试集T多包含一些样本,则训练集S与D差别更大了,被评估的模型与用D训练出的模型相比可能有较大差别,从而降低了评估结果的真实性。(这也是一个问题,可能需要根据数据集的情况对划分比例进行调参。)
交叉验证法
先将数据集划分为k个大小相似的互斥子集,每个子集尽可能保持数据分布的一致性,然后每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集,从而进行k次训练和测试,最终返回的是k个测试结果的均值。
注意点
1.划分方式的不同可能会导致偏差,结果可能不够稳定可靠,可以随机使用不同的划分充分p次,最终得到p次k折交叉验证结果的均值,例如“10次10折交叉验证”
自助法
以自助采样(bootstrap sampling)为基础,对包含m个样本的源数据集进行有放回的m次采样以获得同等规模的训练集。在这m次采样中都不被抽到的概率大约为0.368,也即源数据集中有大约1/3的样本是训练集中没有的。因此,我们可以采用这部分样本作为验证集,所得的结果称为包外估计。
注意点
1.自助法在数据集较小 、难以有效划分训练/测试集时很有用。
2.自助法能从初始数据集中产生多个不同的训练集,这对集成嘘唏等方法很有好处。
3.当然也存在一定的问题,自助法因为改变了初始数据集的分布,会引入估计偏差。
调参与最终模型
在模型评估和选择的过程中,只使用了一部分数据训练模型,在模型选择完成后,学习算法和参数已经确定了,此时用数据集D重新训练,该过程中使用了所有m个样本,得到最终模型。
注意区分验证集和测试集:测试集用来评估模型在实际使用时的泛化能力,验证集用来进行模型选择和调参。
性能度量
用来衡量模型泛化能力的评价标准
查准率、查全率和F1
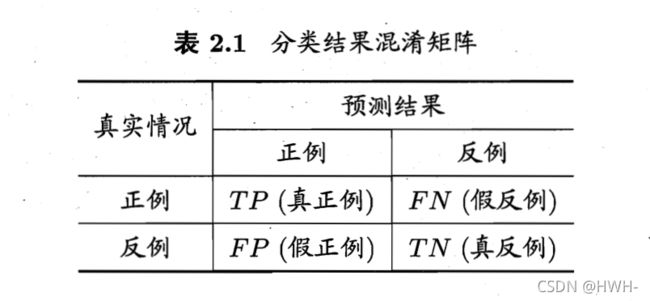
查准率
P = T P T P + F P P = \frac{TP}{TP+FP} P=TP+FPTP
查全率
R = T P T P + F N R = \frac{TP}{TP+FN} R=TP+FNTP
F1 score
1 F 1 = 1 2 × ( 1 P + 1 R ) ⇒ F 1 = 2 × P × R P + R \frac{1}{F1} = \frac{1}{2} \times (\frac{1}{P} + \frac{1}{R}) \Rightarrow F1 = \frac{2 \times P \times R}{P + R} F11=21×(P1+R1)⇒F1=P+R2×P×R
P-R图

平衡点(break-Event Point,BEP)是一个简单的度量
后面部分等之后学习完再更…