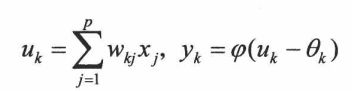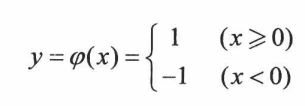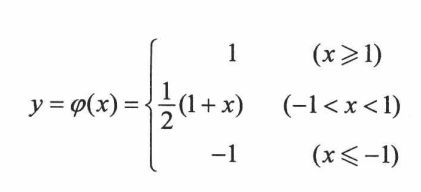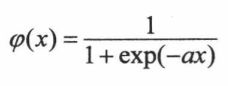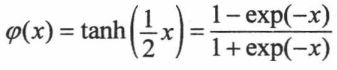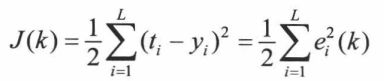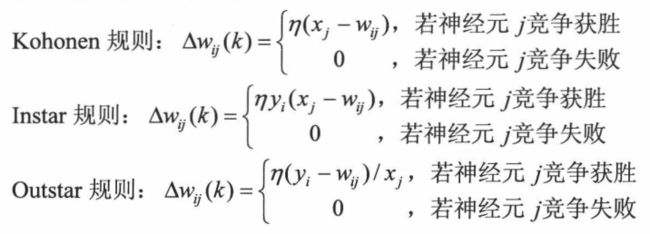人工神经网络/ANN简介
目录
前言
1.什么是训练集、测试集和验证集?
2.人工神经网络和 生物神经元结构对应的理解
3.什么是梯度下降法,在神经网络上如何用于调节权重?
4.为什么神经网络要进行归一化处理?
5.激活函数的形式:
6.NN分类
7.NN的工作过程
8.神经网络的学习方式
9.NN学习算法
10.神经网络分类
前言
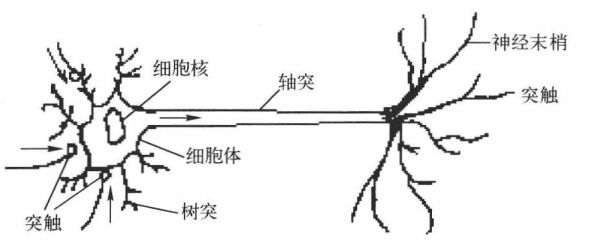
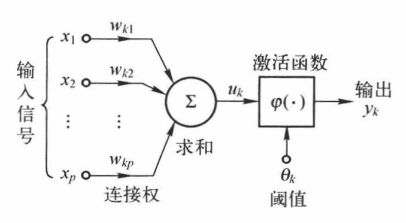
首先理解一下人工神经网络和生物元神经元结构的对应关系:细胞核是新陈代谢的中心,由细胞核、细胞体、树突等组成,树突起着接收输入信号的作用,所以树突对应神经网络的输入层(但是计算神经网络层数的时候,输入层不算层数计入);轴突相当于生物元神经的传输通道,起着信息传递作用,轴突终端的突出是生物神经元之间的连接接口,也可以作为输出,所以对应NN的输出层。
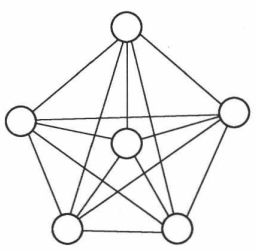
图1 生物元神经网络结构
图2 人工神经元模型
神经网络做预测的本质个人理解:利用训练集(输入和目标输出)让NN不断学习,使其选择到较为精确的权重(weight)、偏值(bias),而权重/连接权/学习因子的调节最常见的是梯度下降法,其本质是目标输出和实际输出的误差平方和(最小二乘法)最小,所以理论上训练集越大,效果越好,学习得到的权重等参数愈加合理,之后利用测试集对学习好的神经网络进行测试,看是否要重新选择训练或者更换激活函数等调试,最后由于训练集不可能无限大包含所有的情况,所以要有验证集对该学习好的神经网络进行鲁棒性验证。好了以上就是自己对网络训练的浅显理解,如有不到位的地方,欢迎指导交流,谢谢!
给出以下链接参考,有兴趣读者可以查阅:
1.什么是训练集、测试集和验证集?
机器学习为什么要划分训练集、测试集和验证集?这3个样本集的区别又在哪里? - 知乎
2.人工神经网络和 生物神经元结构对应的理解
秒懂,神经网络(NN)_哔哩哔哩_bilibili
3.什么是梯度下降法,在神经网络上如何用于调节权重?
[5分钟深度学习] #01 梯度下降算法_哔哩哔哩_bilibili
4.为什么神经网络要进行归一化处理?
:因为激活函数起着非线性映射的作用,即神经网络的非线性逼近能力,而输入的求和通常是线性求和(线性组合),所以为了避免映射跑偏,一般将限制在(0,1)或者(-1,1)之间,所以上面的NN数学模型即可简单的表述为:
其中:wkj表示第k个神经元的第i个输入权值;xj为第j个输入;uk为输入线性组合结果;φ(.)为激活函数;yk为第k个神经元的实际输出。θk(bk)为阈值/偏值,通常用于权重的调节。
5.激活函数的形式:
(1)阶跃函数:
(2)分段线性函数:
(3)s型函数
①sigmoid非对称s函数:
②双曲正切中心对称s函数 :
6.NN分类
从功能上来看,神经网络按连接方式可分为前馈型网络和反馈型网络:
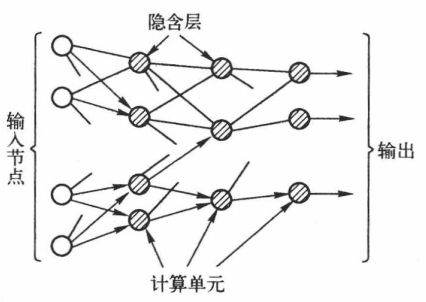
(1)前馈神经网络:即没有反馈,前面一层输出(可以输出到多个神经元作为其输入,当然也可以直接作为输出层输出)到后面一层,后面的输入不会反馈到前一层,所以它的节点分为输入单元和计算单元,且计算单元可以有任意个输入,但是只有一个输出。
(2)反馈型神经网络:又称递归神经网络或回归神经网络,其所有的节点都是计算单元,可以同时接收输入,可以有多个输出,其网络可以堪称一个无向图。
7.NN的工作过程
主要分为两个阶段:
①学习阶段:此时通过训练集学习对连接权的权值进行修改
②工作阶段:对学习阶段学习好的网络用于实战
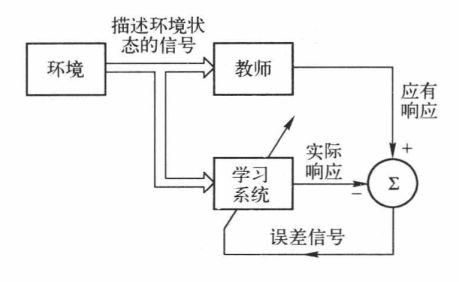
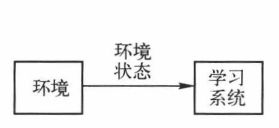
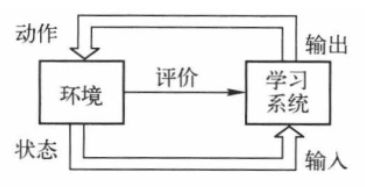
8.神经网络的学习方式
按环境所提供信息量的大小可分为三种:
①有监督/有教师学习:即存在若干个输入和目标输出组成的训练样本/训练集进行学习,所谓的“教师”即目标输出,通过实际输出与目标输出比较来调整权值和阈值,使实际输出越来越接近目标输出。
②无监督学习/无教师学习:这是一组自组织过程,没有目标输出,貌似没有学习的目的,但是这种类型的算法通过完成聚类操作,即学会将输入划分成某些类型,所以适合量化等应用问题。
③强化学习(再励学习):这种学习机制介于两者之间,外部环境对输出结果只给出奖罚等评价而不给出正确答案,即输入对应某个区间等级,所以适应控制系统领域。
9.NN学习算法
(1)δ学习规则(误差纠正学习规则):即给定一个误差目标函数J(通常为均方误差),通过最小化这个目标函数使神经网络学习得到的实际输出在误差内接近目标函数的目的。
其中t_ik为第i个神经元在时刻的期望输出,y为实际输出,由于y由学习中的权重决定,所以问题进而转变为求使J为极小值时自变量权重,根据最速梯度下降法得到权重为:
其中η为学习速率也是梯度下降法的搜索补偿(0<η≤1),f(.)为激活函数,x为输入
(2)Hebb学习规则:当某一突触两端的神经元同为激活同步时(同为激活或抑制),连接强度增强,反之减弱。所以是一种无监督的学习规则,即不需要目标函数的任何相关信息。那么这样就无法对学习的权值进行调整。所以增加一个衰减项-dr*w:
其中,衰减系数dr∈[0 1]。
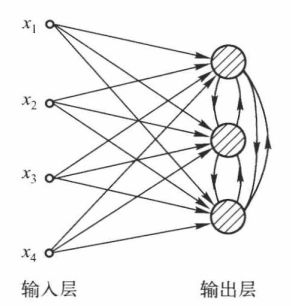
(3)竞争学习规则:即多个输出单元相互竞争,最强激活的单元(将其他输出单元抑制住)作为唯一输出。竞争学习网络结构如下所示:
最常见的竞争学习规则有如下几种:
10.神经网络分类
①MP神经网络
②神经感知机神经网络/感知机
③自适应神经网络
④反向传播(BP)神经网络
⑤径向基(RBF)神经网络
⑥自组织竞争神经网络
⑦自组织特征映射(SOM)神经网络
⑧反传(CPN)神经网络
⑨自适应共振理论(ATR)神经网络
⑩学习向量量化(LVQ)神经网络
(11)Elman神经网络
(12)Hopfield神经网络
(13)Botlzmann神经网络