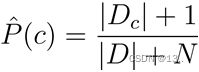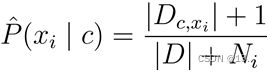朴素贝叶斯分类垃圾邮件
贝叶斯定理
已知两个独立事件A和B,事件B发生的前提下,事件A发生的概率可以表示为P(A|B),即:
P(A) 称为”先验概率”,即在B事件发生之前,我们对A事件概率的一个判断。如:正常收到一封邮件,该邮件为垃圾邮件的概率就是“先验概率”。
P(A|B)称为”后验概率”, 即在B事件发生之后,我们对A事件概率的重新评估。如:邮件中含有“中奖”这个词,该邮件为垃圾邮件的概率就是“后验概率”。
朴素贝叶斯分类器
朴素贝叶斯分类器(Naïve Bayes Classifier)采用了“属性条件独立性假设”,即每个属性独立地对分类结果发生影响。为方便公式标记,不妨记P(C=c|X=x)为P(c|x),基于属性条件独立性假设,贝叶斯公式可重写为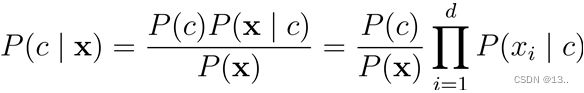
其中d为属性数目,x_i 为 x 在第i个属性上的取值
结果
用p1(x,y)表示数据点(x,y)属于类别1的概率,用p2(x,y)表示数据点(x,y)属于类别2的概率,那么对于点(x,y), 如果 p1(x,y) > p2(x,y),那么类别为1;如果 p2(x,y) > p1(x,y),那么类别为2。
拉普拉斯修正
若某个属性值在训练集中没有与某个类同时出现过,则训练后的模型会出现 over-fitting 现象。假如我们进行判断的词有“中奖”、“免费”、“恭喜您被抽中”,比如“词=福利”,训练集中没有该样例,因此连乘式计算的概率值为0,无论其他属性上明显像正常邮件,分类结果都是“垃圾邮件”,这显然不合理。为了避免其他属性携带的信息,被训练集中未出现的属性值“抹去”,在估计概率值时通常要进行“拉普拉斯修正”:令 N 表示训练集 D 中可能的类别数,N_i表示第i个属性可能的取值数,则贝叶斯公式可修正为:
代码实现
import os
import re
import string
import math
DATA_DIR = 'enron'
target_names = ['ham', 'spam']
def get_data(DATA_DIR):
subfolders = ['enron%d' % i for i in range(1,7)]
data = []
target = []
for subfolder in subfolders:
# spam
spam_files = os.listdir(os.path.join(DATA_DIR, subfolder, 'spam'))
for spam_file in spam_files:
with open(os.path.join(DATA_DIR, subfolder, 'spam', spam_file), encoding="latin-1") as f:
data.append(f.read())
target.append(1)
# ham
ham_files = os.listdir(os.path.join(DATA_DIR, subfolder, 'ham'))
for ham_file in ham_files:
with open(os.path.join(DATA_DIR, subfolder, 'ham', ham_file), encoding="latin-1") as f:
data.append(f.read())
target.append(0)
return data, target
X, y = get_data(DATA_DIR)
class SpamDetector_1(object):
"""Implementation of Naive Bayes for binary classification"""
#清除空格
def clean(self, s):
translator = str.maketrans("", "", string.punctuation)
return s.translate(translator)
#分开每个单词
def tokenize(self, text):
text = self.clean(text).lower()
return re.split("\W+", text)
#计算某个单词出现的次数
def get_word_counts(self, words):
word_counts = {}
for word in words:
word_counts[word] = word_counts.get(word, 0.0) + 1.0
return word_counts
class SpamDetector_2(SpamDetector_1):
# X:data,Y:target标签(垃圾邮件或正常邮件)
def fit(self, X, Y):
self.num_messages = {}
self.log_class_priors = {}
self.word_counts = {}
# 建立一个集合存储所有出现的单词
self.vocab = set()
# 统计spam和ham邮件的个数
self.num_messages['spam'] = sum(1 for label in Y if label == 1)
self.num_messages['ham'] = sum(1 for label in Y if label == 0)
# 计算先验概率,即所有的邮件中,垃圾邮件和正常邮件所占的比例
self.log_class_priors['spam'] = math.log(
self.num_messages['spam'] / (self.num_messages['spam'] + self.num_messages['ham']))
self.log_class_priors['ham'] = math.log(
self.num_messages['ham'] / (self.num_messages['spam'] + self.num_messages['ham']))
self.word_counts['spam'] = {}
self.word_counts['ham'] = {}
for x, y in zip(X, Y):
c = 'spam' if y == 1 else 'ham'
# 构建一个字典存储单封邮件中的单词以及其个数
counts = self.get_word_counts(self.tokenize(x))
for word, count in counts.items():
if word not in self.vocab:
self.vocab.add(word)#确保self.vocab中含有所有邮件中的单词
# 下面语句是为了计算垃圾邮件和非垃圾邮件的词频,即给定词在垃圾邮件和非垃圾邮件中出现的次数。
# c是0或1,垃圾邮件的标签
if word not in self.word_counts[c]:
self.word_counts[c][word] = 0.0
self.word_counts[c][word] += count
MNB = SpamDetector_2()
MNB.fit(X[100:], y[100:])
class SpamDetector(SpamDetector_2):
def predict(self, X):
result = []
flag_1 = 0
# 遍历所有的测试集
for x in X:
counts = self.get_word_counts(self.tokenize(x)) # 生成可以记录单词以及该单词出现的次数的字典
spam_score = 0
ham_score = 0
flag_2 = 0
for word, _ in counts.items():
if word not in self.vocab: continue
#下面计算P(内容|垃圾邮件)和P(内容|正常邮件),所有的单词都要进行拉普拉斯平滑
else:
# 该单词存在于正常邮件的训练集和垃圾邮件的训练集当中
if word in self.word_counts['spam'].keys() and word in self.word_counts['ham'].keys():
log_w_given_spam = math.log(
(self.word_counts['spam'][word] + 1) / (sum(self.word_counts['spam'].values()) + len(self.vocab)))
log_w_given_ham = math.log(
(self.word_counts['ham'][word] + 1) / (sum(self.word_counts['ham'].values()) + len(
self.vocab)))
# 该单词存在于垃圾邮件的训练集当中,但不存在于正常邮件的训练集当中
if word in self.word_counts['spam'].keys() and word not in self.word_counts['ham'].keys():
log_w_given_spam = math.log(
(self.word_counts['spam'][word] + 1) / (sum(self.word_counts['spam'].values()) + len(self.vocab)))
log_w_given_ham = math.log( 1 / (sum(self.word_counts['ham'].values()) + len(
self.vocab)))
# 该单词存在于正常邮件的训练集当中,但不存在于垃圾邮件的训练集当中
if word not in self.word_counts['spam'].keys() and word in self.word_counts['ham'].keys():
log_w_given_spam = math.log( 1 / (sum(self.word_counts['spam'].values()) + len(self.vocab)))
log_w_given_ham = math.log(
(self.word_counts['ham'][word] + 1) / (sum(self.word_counts['ham'].values()) + len(
self.vocab)))
# 把计算到的P(内容|垃圾邮件)和P(内容|正常邮件)加起来
spam_score += log_w_given_spam
ham_score += log_w_given_ham
flag_2 += 1
# 最后,还要把先验加上去,即P(垃圾邮件)和P(正常邮件)
spam_score += self.log_class_priors['spam']
ham_score += self.log_class_priors['ham']
# 最后进行预测,如果spam_score > ham_score则标志为1,即垃圾邮件
if spam_score > ham_score:
result.append(1)
else:
result.append(0)
flag_1 += 1
return result
MNB = SpamDetector()
MNB.fit(X[100:], y[100:])
pred = MNB.predict(X[:100])
true = y[:100]
accuracy = 0
for i in range(100):
if pred[i] == true[i]:
accuracy += 1
print(accuracy) # 0.98参考文献(12条消息) 基于朴素贝叶斯的垃圾邮件分类Python实现_random1548的博客-CSDN博客_基于python的邮件分类系统(12条消息) 基于朴素贝叶斯的垃圾分类算法(Python实现)_仁者乐山智者乐水的博客-CSDN博客_垃圾分类算法(12条消息) 通俗易懂的机器学习——筛选垃圾邮件(贝叶斯分类)_艾醒(AiXing-w)的博客-CSDN博客_机器学习垃圾邮件分类(12条消息) 基于朴素贝叶斯模型进行垃圾邮件的分类_几窗花鸢的博客-CSDN博客_基于朴素贝叶斯算法对邮件进行分类