遗传算法的原理与python实现

一、整体理解

遗传算法的思想就是物竞天择，适者生存，通过N代的遗传、变异、交叉、复制，进化出问题的最优解。举个简单的例子(可能不太恰当，理解就行)：假设有一群猫，有一种病毒，有的猫对这种病毒免疫，而有的猫不免疫，我们想让所有的猫都具有抗病毒能力，那就将这些猫放在这种病毒环境中，则具有免疫病毒能力的猫活了下来，不具有抗病毒能力的猫死了，经过繁衍、迭代，到最后只剩下抗病的猫，因为猫把抗病毒这个优秀基因留给了后代。

二、相关概念

相关概念如下：

1、基因和染色体：比如针对z = sinx + cosy求最值的数学问题，每输入一个x和一个y，就会得到一个解z，这个z就叫做可行解，我们可以称为染色体，一个可行解一般由多种元素构成，那么这每一个元素就被称为染色体上的一个“基因”。本例中z是由x和y构成的，那么这x和y这两个元素就被称为染色体上的“基因”。
2、适应度函数：在自然界中，似乎存在着一个上帝，它能够选择出每一代中比较优良的个体，而淘汰一些环境适应度较差的个人。那么在遗传算法中，如何衡量染色体的优劣呢？这就是由适应度函数完成的。适应度函数在遗传算法中扮演者这个“上帝”的角色。比如z = sinx + cosy求最值就是一个适应度函数，我们要找的是z的最值，z的最值对应的x坐标和y坐标就是优良基因。
3、交叉：遗传算法每一次迭代都会生成N条染色体，在遗传算法中，这每一次迭代就被称为一次“进化”。那么，每次进化新生成的染色体是如何而来的呢？——答案就是“交叉”，你可以把它理解为交配。
交叉的过程需要从上一代的染色体中寻找两条染色体，一条是爸爸，一条是妈妈。然后将这两条染色体的某一个位置切断，并拼接在一起，从而生成一条新的染色体。这条新染色体上即包含了一定数量的爸爸的基因，也包含了一定数量的妈妈的基因。(这个在后面的实例中自然会明白)。
4、轮盘赌算法：如何从上一代染色体中选出爸爸和妈妈的基因呢？这不是随机选择的，一般是通过轮盘赌算法完成。在每完成一次进化后，都要计算每一条染色体的适应度，然后采用如下公式计算每一条染色体的适应度概率。那么在进行交叉过程时，就需要根据这个概率来选择父母染色体。适应度比较大的染色体被选中的概率就越高。这也就是为什么遗传算法能保留优良基因的原因。

染色体i被选择的概率 = 染色体i的适应度 / 所有染色体的适应度之和

例如：此时有5个个体，我们知道了其自适应度值 fi ，那么我们可以通过计算第i个个体的前i个适应度之和 qi，最终得到轮盘赌的各区域分界值：(界限值，不是占比)


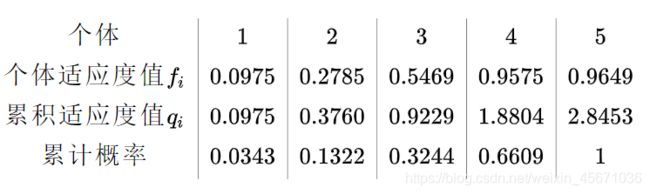
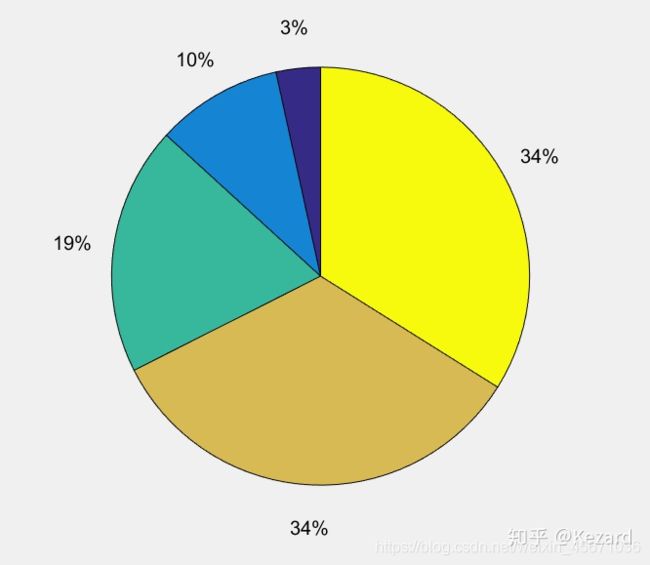
注意：累计适应度即为上面定义的 ,累积概率就是在 qi 的基础之上除以全体适应度值之和:也就是qN ,该例中N取5，显然，个体的适应度值越大，其累计概率就越大，最终轮盘赌操作就按照累计概率为依据，随机产生一个0到1之间的随机数，假设是0.3，那么0.3恰好在累计概率[0.1322,0.3244]之间，那么该轮选择就选择出区间的右端点代表的个体3，反复进行该操作，最终选择出子代种群。(代码中会有这个随机数)
5、变异：类似于生物中的基因突变。交叉能保证每次进化留下优良的基因，但它仅仅是对原有的结果集进行选择，基因还是那么几个，只不过交换了他们的组合顺序。这只能保证经过N次进化后，计算结果更接近于局部最优解，而永远没办法达到全局最优解，为了解决这一个问题，我们需要引入变异。
7、复制：每次进化中，为了保留上一代优良的染色体，需要将上一代中适应度最高的几条染色体直接原封不动地复制给下一代。假设每次进化都需生成N条染色体，那么每次进化中，通过交叉方式需要生成N-M条染色体，剩余的M条染色体通过复制上一代适应度最高的M条染色体而来。
8、染色体中的编码与解码：为了在计算机中进行算法解的搜索，我们需要将解所在空间映射到基因型的空间，这样计算机才能有效的进行识别，解码则反之，是从基因型到解所在区间的映射。一般地，我们采用二进制方式来进行编码，它采用一个二进制的字符串来表征解（包含0或1，即可视为染色体上的基因）在精度允许的前提条件下，二进制编码可以将区间内的无穷多个点用间隔足够小的有限个点来代替。在编码的过程当中，我们需要确定解的区间以及需要表示的解的精度：

初始种群的各个个体的基因可以用均匀分布的随机数产生，例如要在区间x属于 [a,b] 内寻找最优解，那么此时染色体的编码长度，及x的精度要求就至关重要了，假设需要编码的染色体长度为n,要求达到的精度维小数点后m位，那么染色体编码长度和精度之间有如下关系：

在相关精度要求之下，根据上述不等式就可以确定染色体的编码长度n，进而实现对自变量 x 的编码：

在求解个体的自适应函数值时，便需要对染色体编码进行解码（decode），对于一个长度为n的二进制字符串，解码后的x值为：

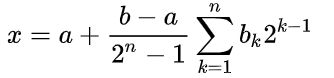
其中的 b1,b2,…bn为个体的二进制编码第k位（从右往左）上的编码数字（0或1），在上述的编码(encode)和解码(decode)定义便实现了解空间和基因空间元素之间的转化。在实际的应用中，二进制也会存在一些问题，比如 x为15和16时，二进制编码为01111和10000，在二进制格式下，两数的转化就需要改变所有位，那么在后续的交叉和变异操作中就会存在缺陷，所以在有的情况下会采用格雷码或其他的编码方式，见这里。

有关概念相关的知识点可以参考如下两个链接：
链接一：遗传算法1（GA）—基础概念及算法流程

链接二：10分钟搞懂遗传算法(含源码)

三、遗传算法大致流程

1、产生初始群体。二进制编码时可确定编码的长度和0，1的含义。
2、计算个体适应度值。(注意：需要将二进制转化为对应区间的十进制)
3、轮盘赌选择
4、交叉、变异运算
5、产生新一代群体
6、迭代

四、代码解析

代码参考的是这里。
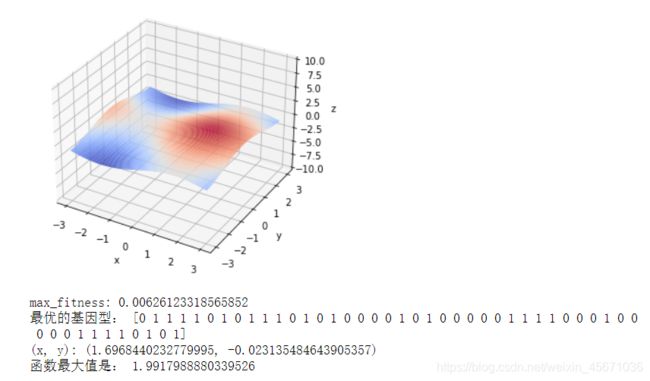
这里我们以求函数z = sinx + cosy的最大值为例，用遗传算法求得最优解。该函数的图像如下图所示，可见该函数的最大值在1.5~2.0之间。

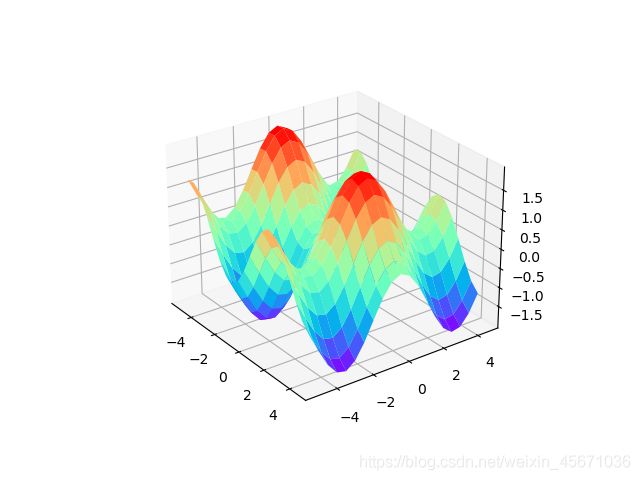
下面是用遗传算法求解的python代码：
第一步：导入python相关库

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

第二步：设置超参数

DNA_SIZE = 24
POP_SIZE = 200
CROSSOVER_RATE = 0.8
MUTATION_RATE = 0.005
N_GENERATIONS = 50
X_BOUND = [-3, 3]
Y_BOUND = [-3, 3]

下面解释一下每个超参数的含义：
DNA_SIZE ：是每个基因的二进制长度，因为有两个基因x和y，所以单个染色体长度为2*DNA_SIZE，则本题中二进制编码矩阵的每一行有48个数值。

POP_SIZE ：种群数目，由DNA_SIZE我们可以知道每一行共有48个二进制编码，而由POP_SIZE我们 可以知道一共有多少行，也就是有多少个个体，还可以说是有多少个可行解。

CROSSOVER_RATE：发生交叉的概率。

MUTATION_RATE：发生基因突变的概率，也可说是变异的概率。具体表现形式是子代的某个基因上的一个二进制编码由原来的1变成了0，或者由0变成了1。

N_GENERATIONS：迭代的次数，即是繁衍了多少代。

X_BOUND ：基因x的取值范围。

Y_BOUND：基因y的取值范围。(也就是说在x,y属于[-3,3]的情况下，z的最大值。)

第三步：定义适应度函数

因为要求的最优解是函数z的最大值，因此适应度函数就是z = sinx + cosy。

def F(x, y):
    return np.sin(x)+np.cos(y)

第四步：定义种群矩阵

def translateDNA(pop):     #pop表示种群矩阵，一行表示一个二进制编码表示的DNA，矩阵的行数为种群数目
    x_pop = pop[:,1::2]    #奇数列表示X
    y_pop = pop[:,::2]     #偶数列表示y
    
    #pop:(POP_SIZE,DNA_SIZE)*(DNA_SIZE,1) --> (POP_SIZE,1)
    x = x_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(X_BOUND[1]-X_BOUND[0])+X_BOUND[0]
    y = y_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(Y_BOUND[1]-Y_BOUND[0])+Y_BOUND[0]
    return x,y  

pop是种群矩阵，是我们用随机数生成的，矩阵大小是[POP_SIZE , DNA_SIZE*2], 即[200，48]，矩阵中的每个位置都是由1或者0填充的。见下图：

x_pop.dot(…)内部数学计算如下图所示：

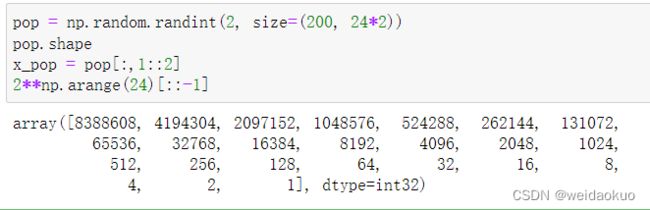
备注：先回顾一下二进制解码公式，见下图：

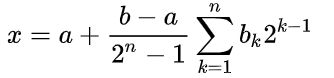
X_BOUND[1]-X_BOUND[0]是区间长度，为6，X_BOUND[0]为-3，也就是说：

x_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)

对应上面公式中的求和部分除以2的n次方减1项，就是将二进制的基因x和y转化为十进制的0到1之间。然后在通过后面的乘以区间长度(b-a)和加上区间最小值(a)，找到其在[-3,3]对应的位置。

总之，该函数的目的是将二进制的x和y转换成在[-3，3]之间，此时x和y的shape为(24,)。

第五步：获取轮盘赌的区域分界值

def get_fitness(pop): 
    x,y = translateDNA(pop)
    pred = F(x, y)                          #减去最小的适应度是为了防止适应度出现负数，通过这一步fitness的范围
    return (pred - np.min(pred)) + 1e-3    #为[0, np.max(pred)-np.min(pred)],最后在加上一个很小的数防止出现为0的适应度

该步骤的目的参考前面轮盘赌的概念。

第六步：交叉

def crossover_and_mutation(pop, CROSSOVER_RATE = 0.8):
    new_pop = []
    for father in pop:                                             #遍历种群中的每一个个体，将该个体作为父亲
        child = father                                          #孩子先得到父亲的全部基因（这里我把一串二进制串的那些0，1称为基因）
        if np.random.rand() < CROSSOVER_RATE:                             #产生子代时不是必然发生交叉，而是以一定的概率发生交叉
            mother = pop[np.random.randint(POP_SIZE)]                #再种群中选择另一个个体，并将该个体作为母亲
            cross_points = np.random.randint(low=0, high=DNA_SIZE*2)            #随机产生交叉的点
            child[cross_points:] = mother[cross_points:]                    #孩子得到位于交叉点后的母亲的基因
        mutation(child) 
        new_pop.append(child)                                               #每个后代有一定的机率发生变异
    return new_pop

第七步：变异

def mutation(child, MUTATION_RATE=0.003):
    if np.random.rand() < MUTATION_RATE:                 #以MUTATION_RATE的概率进行变异
        mutate_point = np.random.randint(0, DNA_SIZE)    #随机产生一个实数，代表要变异基因的位置
        child[mutate_point] = child[mutate_point]^1      #将变异点的二进制为反转

第八步：获取最大值所在的基因片段

def select(pop, fitness):    # nature selection wrt pop's fitness
    idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
                           p=(fitness)/(fitness.sum()) )
    return pop[idx]

第九步：打印结果

def print_info(pop):
    fitness = get_fitness(pop)
    max_fitness_index = np.argmax(fitness)
    print("max_fitness:", fitness[max_fitness_index])
    x,y = translateDNA(pop)
    print("最优的基因型：", pop[max_fitness_index])
    print("(x, y):", (x[max_fitness_index], y[max_fitness_index]))
    print('函数最大值是：', (F(x[max_fitness_index], y[max_fitness_index])))

完整版代码和结果

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

DNA_SIZE = 24
POP_SIZE = 200
CROSSOVER_RATE = 0.8
MUTATION_RATE = 0.005
N_GENERATIONS = 50
X_BOUND = [-3, 3]
Y_BOUND = [-3, 3]

def F(x, y):
    return np.sin(x)+np.cos(y)

def plot_3d(ax):

    X = np.linspace(*X_BOUND, 100)
    Y = np.linspace(*Y_BOUND, 100)
    X,Y = np.meshgrid(X, Y)
    Z = F(X, Y)
    ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap=cm.coolwarm)
    ax.set_zlim(-10,10)
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('z')
    plt.pause(3)
    plt.show()

def translateDNA(pop):     #pop表示种群矩阵，一行表示一个二进制编码表示的DNA，矩阵的行数为种群数目
    x_pop = pop[:,1::2]   #奇数列表示X
    y_pop = pop[:,::2]    #偶数列表示y
    
    #pop:(POP_SIZE,DNA_SIZE)*(DNA_SIZE,1) --> (POP_SIZE,1)
    x = x_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(X_BOUND[1]-X_BOUND[0])+X_BOUND[0]
    y = y_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(Y_BOUND[1]-Y_BOUND[0])+Y_BOUND[0]
    return x,y          # 得到了十进制的x和y，x的大小是24，y的大小也是24

def get_fitness(pop): 
    x,y = translateDNA(pop)
    pred = F(x, y)                          #减去最小的适应度是为了防止适应度出现负数，通过这一步fitness的范围
    return (pred - np.min(pred)) + 1e-3    #为[0, np.max(pred)-np.min(pred)],最后在加上一个很小的数防止出现为0的适应度

def crossover_and_mutation(pop, CROSSOVER_RATE = 0.8):
    new_pop = []
    for father in pop:                                             #遍历种群中的每一个个体，将该个体作为父亲
        child = father                                          #孩子先得到父亲的全部基因（这里我把一串二进制串的那些0，1称为基因）
        if np.random.rand() < CROSSOVER_RATE:                             #产生子代时不是必然发生交叉，而是以一定的概率发生交叉
            mother = pop[np.random.randint(POP_SIZE)]                #再种群中选择另一个个体，并将该个体作为母亲
            cross_points = np.random.randint(low=0, high=DNA_SIZE*2)            #随机产生交叉的点
            child[cross_points:] = mother[cross_points:]                    #孩子得到位于交叉点后的母亲的基因
        mutation(child) 
        new_pop.append(child)                                               #每个后代有一定的机率发生变异
    return new_pop

def mutation(child, MUTATION_RATE=0.003):
    if np.random.rand() < MUTATION_RATE:                 #以MUTATION_RATE的概率进行变异
        mutate_point = np.random.randint(0, DNA_SIZE)    #随机产生一个实数，代表要变异基因的位置
        child[mutate_point] = child[mutate_point]^1      #将变异点的二进制为反转

def select(pop, fitness):    # nature selection wrt pop's fitness
    idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
                           p=(fitness)/(fitness.sum()) )
    return pop[idx]

def print_info(pop):
    fitness = get_fitness(pop)
    max_fitness_index = np.argmax(fitness)
    print("max_fitness:", fitness[max_fitness_index])
    x,y = translateDNA(pop)
    print("最优的基因型：", pop[max_fitness_index])
    print("(x, y):", (x[max_fitness_index], y[max_fitness_index]))
    print('函数最大值是：', (F(x[max_fitness_index], y[max_fitness_index])))

if __name__ == "__main__":
    fig = plt.figure()
    ax = Axes3D(fig)
    plt.ion()#将画图模式改为交互模式，程序遇到plt.show不会暂停，而是继续执行
    plot_3d(ax)

    pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE*2)) #matrix (POP_SIZE, DNA_SIZE)
    for _ in range(N_GENERATIONS):#迭代N代
        x,y = translateDNA(pop)
        if 'sca' in locals(): 
            sca.remove()
        sca = ax.scatter(x, y, F(x,y), c='black', marker='o');plt.show();plt.pause(0.1)
        pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))
        #F_values = F(translateDNA(pop)[0], translateDNA(pop)[1])#x, y --> Z matrix
        fitness = get_fitness(pop)
        pop = select(pop, fitness) #选择生成新的种群

    print_info(pop)
    plt.ioff()
    plot_3d(ax)

显示结果图下：

可见，函数z的最大值约为1.99，还是挺准确的。