格兰杰因果 / EEG脑电数据分析
(因为处理数据的时候需要用到格兰杰因果关系检验,相关的文献里又没有详细解释,但看格兰杰因果又有一些一知半解,于是自己学了一些相关的东西,整理了一下。)
格兰杰因果关系检验为2003年诺贝尔经济学奖得主克莱夫·格兰杰(Clive W. J. Granger)所开创,用于分析经济变量之间的格兰杰因果关系。他给格兰杰因果关系的定义为“依赖于使用过去某些时点上所有信息的最佳最小二乘预测的方差。”
所以说,这个格兰杰因果其实是一个时间序列计量经济学模型,但它的应用不仅限于计量经济学,比如这里我就用它来分析脑电数据。
于是,说到时间序列,我觉得吧,要想前后真正理清楚思路然后把它和我要做的东西关联起来,我决定自学一把信号与系统的比较浅显的一些概念和数学原理还有EEG脑电信号的处理。
写这个博客是记录自己的思考和学习过程,但想到它也可能有幸被人参考于是,列个大纲,可以根据需要看看。
1.信号与系统的基础概念梳理
什么是信号
定义:消息有用的部分
转换成信号的目的:便于传输、梳理
三大热点:传输、交换、处理
信号处理:特征提取、噪声消除、优化
什么是系统
定义:处理输入,生成想要的输出
信号描述
信号可表示为1/多个变量的函数
即,信号=函数
描述方式 :时域分析、频域分析、波形(函数图像)
信号分类
- 确定&随机
- 周期&非周期
- 连续(模拟信号)与离散(数字信号/抽样信号)
- 一维&多维
- 能量受限&功率受限
典型连续时域信号
复指数信号可分为实、虚两部分。其中,实部包含余弦信号,代表时域,体现信号大小,振幅、波峰等。虚部则为正弦信号代表频域,体现信号方向,频率变化。
抽样信号
描述:很小区间里有很大的值
Sa函数
用处:过滤、处理(小波变换)
脑电信号的分析方法
时域分析法——自回归AR模型
自回归模型是脑电分析中常用的一个传统模型,它会根据采集到的数据的更新不断更新参数,以更好地描述数据,然后在此基础上我们就可以用这个模型来进行谱估计和特征提取等等工作。
在时域空间,AR模型可以表述为一个线性预测问题。
我们假设时间序列是 ![]() ,当前采样值为
,当前采样值为![]() ,这个采样值可以用最邻近的前p个数据x(n-p),x(n-p+1),...,x(n-1)的线性加权和来近似。
,这个采样值可以用最邻近的前p个数据x(n-p),x(n-p+1),...,x(n-1)的线性加权和来近似。
![]() 的预测值即为
的预测值即为
其中p表示的是模型的阶数,![]() 表示的是权重。我们把预测值和实际值的差值称为前向预测的误差,
表示的是权重。我们把预测值和实际值的差值称为前向预测的误差,
对于整个![]() 序列,定义其预测误差功率为预测误差的平方和,于是有
序列,定义其预测误差功率为预测误差的平方和,于是有
对于参数![]() ,一般用最小二乘法估计,目的就是使得我们在用这个p阶模型拟合给定数据的时候,预测误差功率E是最小的。
,一般用最小二乘法估计,目的就是使得我们在用这个p阶模型拟合给定数据的时候,预测误差功率E是最小的。
(这里我就不详细写了,大概思路就是令![]() ,然后我们能得到p个方程的方程组,代入预测误差功率的那个计算公式,得到最小预测误差功率
,然后我们能得到p个方程的方程组,代入预测误差功率的那个计算公式,得到最小预测误差功率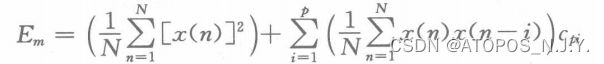 )
)
让我比较头秃的是这个AR参数的自相关估计法,这里定义了一个无穷实数据序列的自相关函数
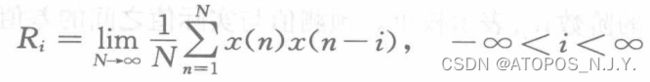 ,可以看到这个东西其实就是在最小预测误差功率的计算公式当中右边括号内的项,但是我确实没理解为什么是这样(早饭吃了鸡蛋,依旧没能捣鼓出来)
,可以看到这个东西其实就是在最小预测误差功率的计算公式当中右边括号内的项,但是我确实没理解为什么是这样(早饭吃了鸡蛋,依旧没能捣鼓出来)
所以我当机立断决定先把参考资料截图,未来可能某天就突然明白了呢。
还有一个问题就是,前面提到了这个模型有一个阶数p,那这个p应该怎么确定呢?从减小计算复杂度的层面考虑应该尽量选用低阶的模型,这个常用的方法就有预测误差准则法和赤池信息准则法AIC。
最终预测误差准则法,它定义AR模型的阶数为使得预测误差功率最小的阶数。假设p阶模型所对应的预测误差功率为![]() ,
,![]()
赤池信息准则也不难理解,它的理念就是最小化信息量,但是信息量是比较抽象的一个概念,在这里可以用似然函数对数的均值估计。于是得到定义![]() ,使得这个式子最小的p就是AR模型的参数。
,使得这个式子最小的p就是AR模型的参数。
格兰杰因果关系检验
格兰杰因果关系检验的统计学本质是对平稳时间序列数据的一种预测。在时间序列情形下,两个经济变量X、Y之间的格兰杰因果关系定义为:若在包含了变量X、Y的过去信息的条件下,对变量Y的预测效果要优于只单独由Y的过去信息对Y进行的预测效果,即变量X有助于解释变量Y的将来变化,则认为变量X是引致变量Y的格兰杰原因。
(其实把格兰杰因果关系检验应用在EEG信号的处理问题上我是有点困惑的,因为在我参考的一些资料当中很多也都提到了进行格兰杰因果关系检验的一个前提条件是时间序列必须具有平稳性,否则可能会出现虚假回归问题,而脑电数据它并不属于平稳的时间序列,maybe分段之后会稍微好一点点?然后我还看到有一个在格兰杰因果关系检验之前首先对各个指标时间序列的平稳性进行单位根检验的东西,我个人觉得吧,这个主要是在计量经济学里会用到的,没有细看)
继续说这个格兰杰因果。上面的内容里已经说了这个AR自回归模型的东西,格兰杰因果关系检验中用到的是受约束回归的思想。就是在这里有一个向量自回归模型,它能够尝试去说明一个变量的当前值受到自身和其他变量的过去值的影响。
由于我的脑电数据是用matlab读取的,所以格兰杰因果关系检验我也想尝试用matlab去实现。
先说一下实现的思路,在这里我们也假设两个时间序列 ![]() 和
和![]() ,然后判断X对Y是否有格兰杰因果关系。步骤如下:
,然后判断X对Y是否有格兰杰因果关系。步骤如下:
首先,把时间序列 ![]() 对所有的滞后项
对所有的滞后项 ![]() 做一个受约束的回归(不包含滞后项
做一个受约束的回归(不包含滞后项 ![]() ),得到受约束的残差平方和RSSR。然后,在回归式中加入滞后项
),得到受约束的残差平方和RSSR。然后,在回归式中加入滞后项 ![]() 做一个无约束的回归,得到无约束的残差平方和RSSUR。
做一个无约束的回归,得到无约束的残差平方和RSSUR。
假设![]() (我的理解就是假设这个x对y的预测没有起到帮助,也就是说我们先假设x不是y的原因)。
(我的理解就是假设这个x对y的预测没有起到帮助,也就是说我们先假设x不是y的原因)。
然后就是上面笔记中写到的去做自回归和联合回归误差的F检验,即:遵循自由度为 ![]() 和
和 ![]() 的 F分布。在这里,
的 F分布。在这里,![]() 是样本容量,
是样本容量,![]() 等于滞后项
等于滞后项 ![]() 的个数,即有约束回归方程中待估参数的个数,
的个数,即有约束回归方程中待估参数的个数,![]() 是无约束回归中待估参数的个数。如果在选定的显著性水平α上计算的F值超过临界值Fα,则拒绝y原假设,我们就可以认为
是无约束回归中待估参数的个数。如果在选定的显著性水平α上计算的F值超过临界值Fα,则拒绝y原假设,我们就可以认为![]() 对
对![]() 有格兰杰因果关系。
有格兰杰因果关系。
其中用到了AIC(赤池信息量)、BIC(贝叶斯信息量)的概念,感觉还没怎么弄明白,先甩个链接放着,等弄明白了再补充叭——(摆烂)https://blog.csdn.net/CHIERYU/article/details/51746554?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522166210106516782428610074%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=166210106516782428610074&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~baidu_landing_v2~default-4-51746554-null-null.142^v44^pc_ran_alice&utm_term=BIC&spm=1018.2226.3001.4187
然后就是代码实现的部分 ——
function granger(x,y,alpha,max_lag)
T = length(x);
BIC = zeros(max_lag,1);
RSSR = zeros(max_lag,1);
i = 1;
while i <= max_lag
ystar = x(i+1:T,:);
xstar = [ones(T-i,1) zeros(T-i,i)];
j = 1;
while j <= i
xstar(:,j+1) = x(i+1-j:T-j);
j = j+1;
end
[~,~,r] = regress(ystar,xstar);
BIC(i,:) = T*log(r'*r/T) + (i+1)*log(T);
RSSR(i,:) = r'*r; % 受约束的残差平方和
i = i+1;
end
x_lag = find(min(BIC));
BIC = zeros(max_lag,1);
RSSUR = zeros(max_lag,1);
i = 1;
while i <= max_lag
ystar = x(i+x_lag+1:T,:);
xstar = [ones(T-(i+x_lag),1) zeros(T-(i+x_lag),x_lag+i)];
j = 1;
while j <= x_lag
xstar(:,j+1) = x(i+x_lag+1-j:T-j,:);
j = j+1;
end
%加入滞后项
j = 1;
while j <= i
xstar(:,x_lag+j+1) = y(i+x_lag+1-j:T-j,:);
j = j+1;
end
[~,~,r] = regress(ystar,xstar);
BIC(i,:) = T*log(r'*r/T) + (i+1)*log(T);
RSSUR(i,:) = r'*r; % 不受约束的残差平方和
i = i+1;
end
y_lag = find(min(BIC));
F_num = ((RSSR(x_lag,:) - RSSUR(y_lag,:))/y_lag);
F_den = RSSUR(y_lag,:)/(T-(x_lag+y_lag+1));
F = F_num/F_den;
c_v = finv(1-alpha,y_lag,(T-(x_lag+y_lag+1))); % 计算p值,参数分别为置信度、组内自由度、组间自由度
p = 1-fcdf(F,y_lag,(T-(x_lag+y_lag+1))); % fcdf()用于计算f分布的累积函数
end
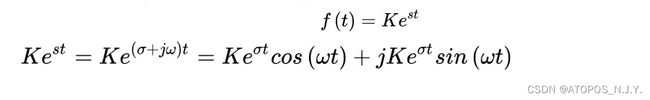
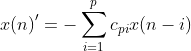
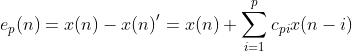
![E = \frac{1}{N}\sum_{n=1}^{N}[x(n)+\sum_{i=1}^{p}c_{pi}x(n-i)]^{2}](http://img.e-com-net.com/image/info8/d916d15058e04d01a16c6f35518d03f1.gif)


