智能优化算法：基于Powell优化的鸽群优化算法

前言

       哈喽，大家好！我是一枚小博士，今天给大家带来的是鸽群优化算法(pigeon-inspired optimization, PIO)的改进策略——组合优化。

一、鸽群优化算法(Pigeon-inspired Optimization)原理

       基本的PIO算法原理，请大家移步上一篇文章智能优化算法：基于量子的鸽群优化算法

二、Powell算法

1. 原理

       鲍威尔法又称方向加速法，它由Powell于1964年提出，是利用共轭方向可以加快收敛速度的性质形成的一种搜索方法。该方法不需要对目标函数进行求导，当目标函数的导数不连续的时候也能应用，因此，鲍威尔算法是一种十分有效的直接搜索法。
Powell法可用于求解一般无约束优化问题，对于维数n<20的目标函数求优化问题，此法可获得较满意的结果。
       不同于其他的直接法，Powell法有一套完整的理论体系，故其计算效率高于其他直接法。该方法使用一维搜索，而不是跳跃的探测步。同时，Powell法的搜索方向不一定为下降方向。

2. 算法流程

Step1: 给定初始点$x^{(0)}$，对算法的搜索精度ε赋值。给定D个线性无关的初始搜索方向$d^{(i)}(i=0,1,\cdots ,D-1)$，一般情况下选择D个坐标轴方向为搜索方向，D的取值与目标函数的维数有关。
Step2：从初始点$x^{(0)}$出发，依次沿着$d^{(0)},d^{(1)},\cdots ,d^{(D-1)}$进行一维搜索，根据公式(1)(2)得到$x^{(1)},x^{(2)},\cdots ,x^{(D)}$，令k=0。
$$f\left(x^{\left(i\right)}+{\alpha }_i{d}^{\left(i\right)}\right)=\underset{\alpha \in S}{\min }f\left(x^{\left(i\right)}+\alpha d^{\left(i\right)}\right)$$
$$X^{\left(i+1\right)}=x^{\left(i\right)}+{\alpha }_i{d}^{\left(i\right)},i=0,1,\cdots ,D$$
其中，${\alpha }_i$与α均为搜索步长，${\alpha }_i$为目标函数一维最优化问题的解。
Step3：令$d^{(D)}=x^{(D)}-x^{(0)}$。若$\Vert d^{(D)}\Vert <\epsilon$，则得到解$x^{(D)}$，计算结束；否则，从$x^{(D)}$出发，沿着$d^{(D)}$进行精确的一维搜索，得到$x^{(D+1)}$。
Step4：根据公式(3)计算一维搜索最快下降量$t_l$为：
$$f\left(x^{(t_l)}\right)-f\left(x^{\left(t_l-1\right)}\right)=\underset{o\le i\le D}{\max }\left\{f\left(x^{\left(i\right)}\right)-f\left(x^{\left(i+1\right)}\right)\right\}$$
Step5：若不等式(4)成立，则表明D个一维搜索方向仍然为线性无关。令$x^{(0)}=x^{(D+1)}，k=k+1$，跳转至step2。
$$f\left(x^{\left(0\right)}\right)-2f\left(x^{\left(D\right)}\right)+f\left(2x^{\left(D\right)}-x^{\left(0\right)}\right)\ge 2\left(f\left(x^{\left(t_l\right)}\right)-f\left(x^{\left(t_l+1\right)}\right)\right)$$
Step6：如果不等式(4)不成立，则表明一维搜索方向线性相关，则令$d^{(t_i+i)}=d^{(t_l+i+1)},i=0,1,\cdots ,D-t_l-1$，确保产生一组新的线性无关搜索方向.。令$x^{(0)}=x^{(D+1)}，k=k+1$，转至Step2。

三、组合策略

       Powell算法计算简单、收敛速度快、不需要计算函数导数，具有较强的局部搜索能力。但Powell算法极度依赖初始点配置，初始值选择的好坏直接影响了算法是否能收敛到全局极小值，甚至导致算法配准失败。因此将鸽群算法优化后的位置信息作为Powell算法初始值，避免Powell搜索失败。
       可以自由设置组合中迭代策略，即每隔n次迭代后，使用Powell算法进行再次优化。

四、仿真实验

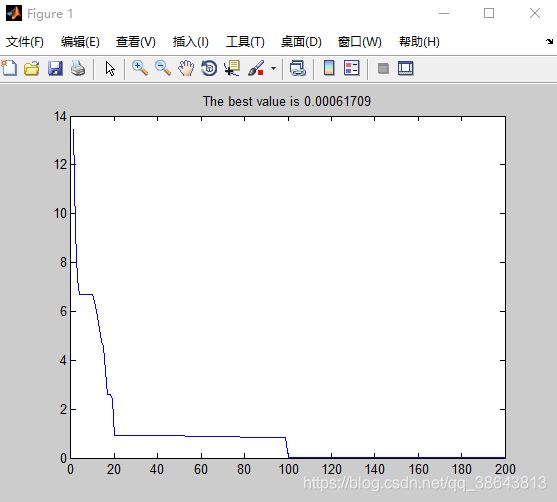
       采用CEC测试函数Ackley对改进前后算法进行测试，目标维度为20维。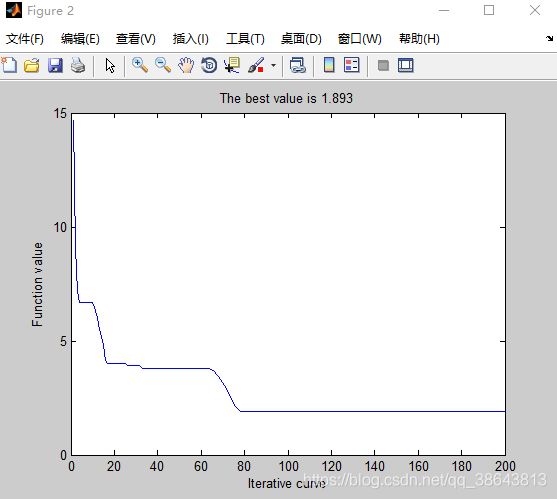

图1. PIO算法

图2. P_PIO算法

五、总结

       通过图1与图2 ，我们可以看出改进前的最优解为1.893，改进后的最优解为 6.1709e-4，根据Powell优化的间隔次数不同，最优优化的效果也不尽相同。但，尽可能不要间隔太小，否则会增加算法的时间复杂度。

六、附件

Powell-PIO算法的Matlab代码链接如下：https://mianbaoduo.com/o/bread/aZ6Xmpo=

原创不易，还请大家看完可以帮忙点赞，拜谢！

       注：好多朋友问我要基本PIO算法代码，我放在下载专栏了，地址为：https://download.csdn.net/download/qq_38643813/13125329大家如果是CSDN会员的话可以直接去下载，如果不是的话也不要破费了，在评论区留下邮箱，我发给你!