H-03卷积神经网络中卷积的作用与原理

目录

1.前言

2.卷积的作用

3.卷积的参数

3.1 卷积核大小（kernel_size）

3.2 填充（padding）

3.2.1 same

3.2.2 valid

3.2.3 full

3.3 卷积核算子（operator）

3.3.1 Robert 算子

3.3.2 Prewitt算子

3.3.3 Sobel 算子

3.3.4 Laplance 算子

3.4 卷积核深度与个数（depth、filter）

3.5 步长（strides）

4.搭建卷积层

---

1.前言

        在神经网络中卷积是最常见的操作，通常情况下它应用在神经网络的Input层后面，所以我们多数情况下称这一层为卷积层或隐藏层，这里提一句什么是隐藏层，在神经网络中有输入层和输出层，这两层对于外界是可见的，并且它接收来自外界的输入或输出到外界里去，当然一个完整的神经网络不可能只有输入层和输出层，就以CNN卷积神经网络来说当图像输入到输入层之后会被传递给下一层做特征提取下一层一般是卷积层，随后卷积层会传递给池化层，在由池化层传递给全连接层，这三层对于外界来说是不可见的，它不能直接接收外界的输入或直接输出到外界，所以通常情况下我们称这些为隐藏层，在神经网络中卷积层一般般称为Conv层，例如处理2维数据一般是conv2d，一维数据就叫conv1d、1d是对时序数据做处理而2d是对空间数据做处理，2d具有x、y。 

2.卷积的作用

        卷积的作用就是为了将Input的数据做一次特征提取，例如下图有一组衣服的图片：

        我们神经网络的目的是为了判断输入目标是上衣还是裤子，或者裙子，那么我们就不需要考虑颜色分量，因为如果只是判断衣服的类型的话可以通过外形判断，那么在输入到全连接层之前可以利用卷积来提取我们想要的数据，过滤掉不需要的数据，这样可以大幅度提升神经网络的准确性以及网络大小，如下图是经过卷积和池化后的一组图片：

        可以看到经过卷积和池化后已经将图像的颜色过滤掉了，只保留的轮廓特征，这样的话就过滤掉我们不需要的颜色特征，这样的特征输入到全连接层里会更加符合我们的业务需求。

        如果需要判断衣服的品牌那么就需要颜色特征，所以我们就需要对卷积做一次优化，让卷积操作尽可能的去提取到图片里的颜色分量，例如修改卷积核的数量。

        卷积的目的就是为了从输入数据中提取我们需要的特征，一般情况下卷积是配合池化层一起使用的，池化层的目的是将卷积提取的特征进行一次筛选，保留最优质的特征，例如如下图片(从左到右分别是：原图、卷积、池化)：

3.卷积的参数

3.1 卷积核大小（kernel_size）

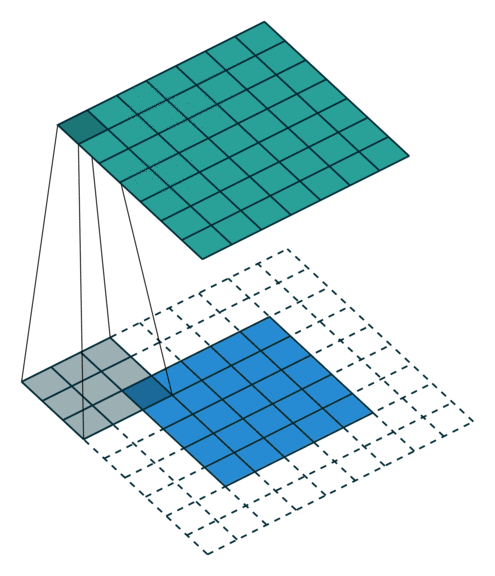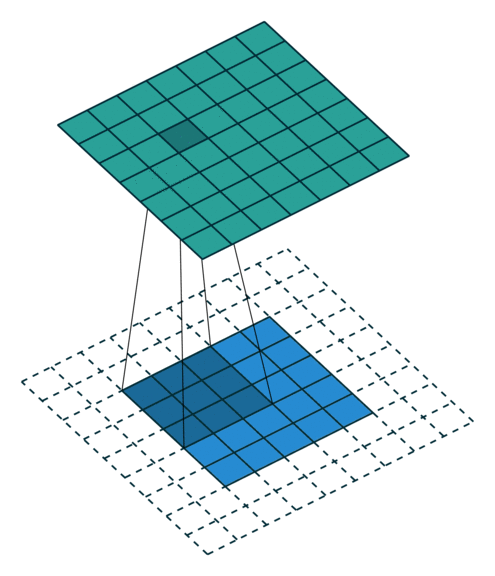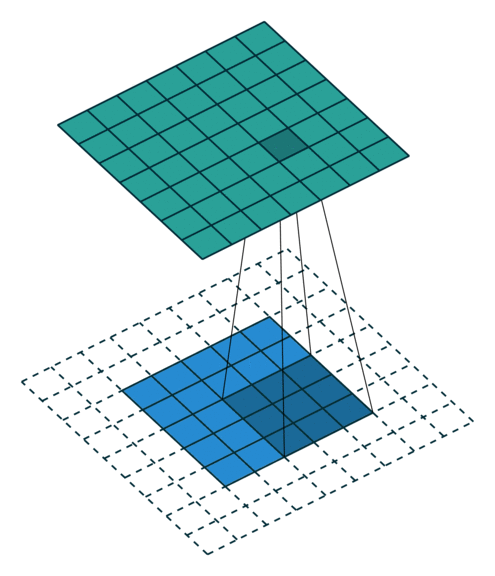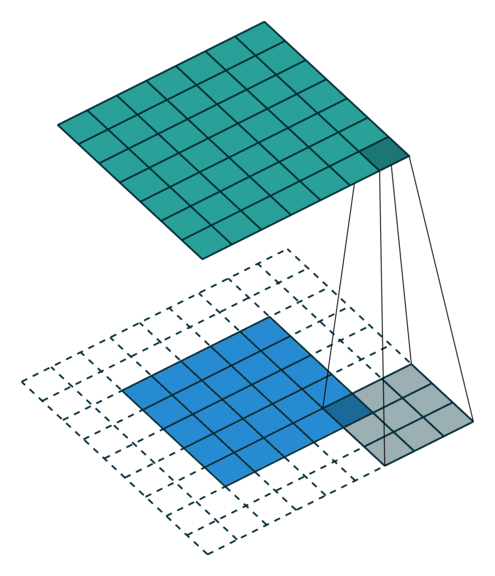
        卷积核的大小是用来控制卷积在提取时的维度，例如下面动图表示当卷积核大小为3x3：

        通过上图可以看到卷积在每次提取数据时都以3*3的维度进行提取，一般卷积核的尺寸是根据padding（填充）方式来决定是奇数还是偶数。

3.2 填充（padding）

        通常情况下当我们在做卷积操作时最常见的卷积核尺寸是：3 x 3、5 * 5、7 * 7，其实这些数是和padding有关，那什么是padding？

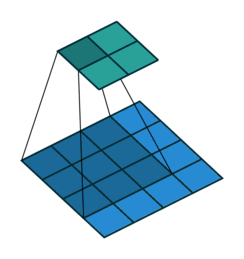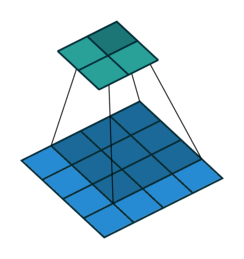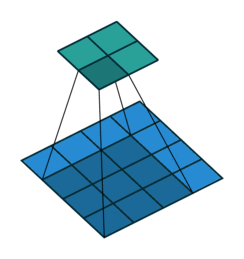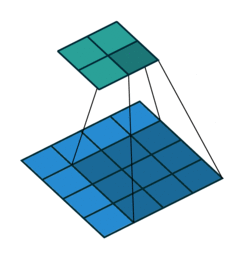
        padding是卷积在进行操作时对边缘进行填充的一种方式，例如下图：

        上图的蓝色部分代表输入数据，维度是4 x 4，淡绿色是卷积后的数据，卷积核大小是3 x 3，可以明显看到卷积后的维度变成了2 x 2导致了卷积维度与原图像维度不一致了，所以我们需要进行一次填充，padding有两种常用的填充方式：same和valid。

3.2.1 same

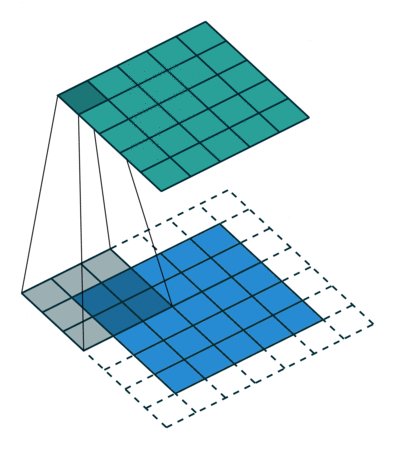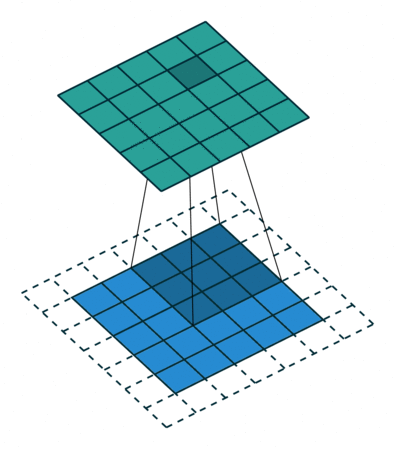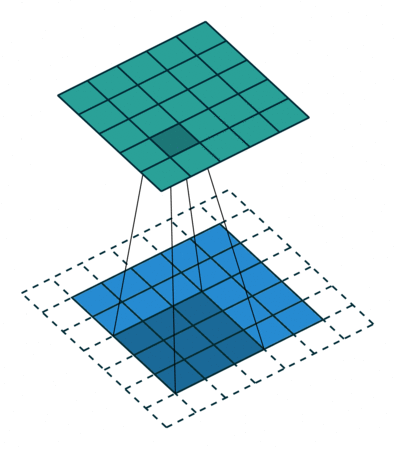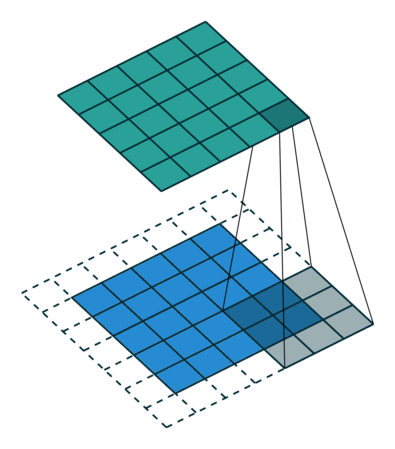
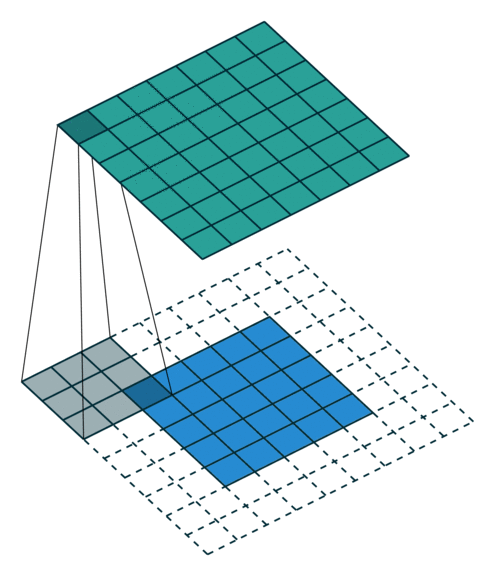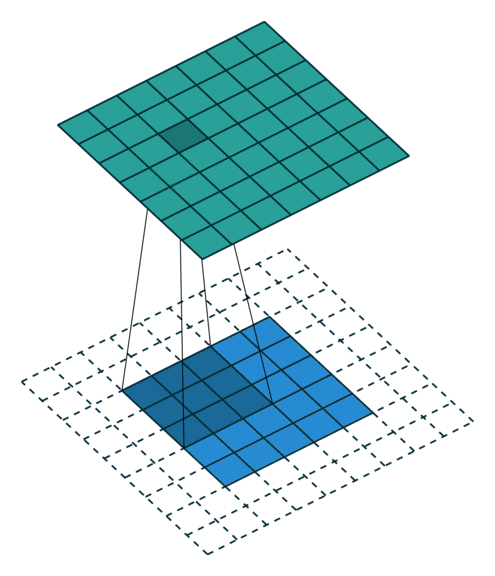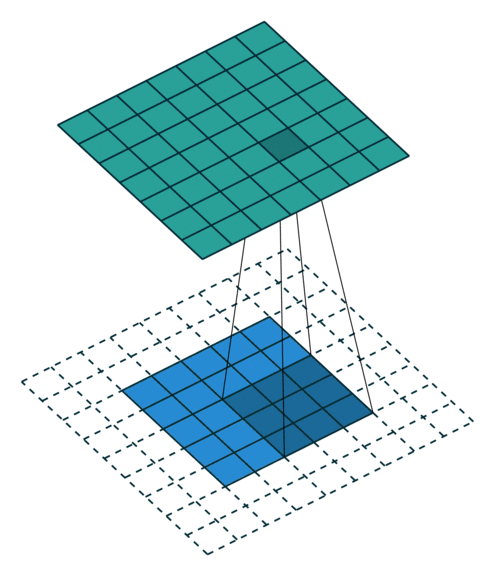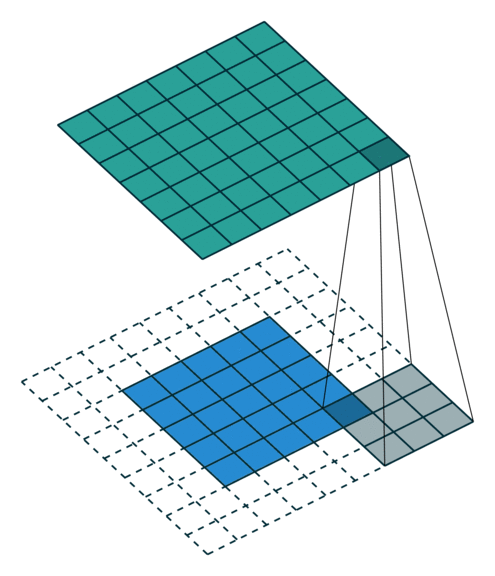
        same是尺寸不变的一种卷积方式，它会保证输出维度与输入维度一致，但不是百分百保证，它会在输入数据边缘填充数据，这些数据通常为0，即填充空白数据，以便让卷积输出尺寸与输入尺寸一致，它是根据你的参数来决定的，下图会更直观的表示same的原理：

        可以看到输入数据的周围出现了白色的方块，这些方块就是same填充的数据，目的是为了保证卷积时输出尺寸与输入尺寸一致，这也意味着边缘特征会被提取多次，保证了特征的准确性。

        同时也可以看到same卷积时锚点在中心位置，只有中心位置与数据重叠交汇时才会进行卷积：

        而奇数刚好拥有天然的中心点，所以如果卷积核的大小是偶数，那么就会扩大运算量，使得神经网络变得慢起来。

        这也就意味着无论当你的卷积核多大，它最终扩大padding时都会以上面的方式来进行卷积，所以卷积核的大小并不会影响输出尺寸，但受到strides的影响。

下面是它计算输出矩阵大小的C实现：

 case Padding::SAME:
    *new_height = ceil(in_height / static_cast(row_stride));
    *new_width = ceil(in_width / static_cast(col_stride));
    const int pad_needed_height = (*new_height - 1) * row_stride + filter_height - in_height;
    *pad_top = pad_needed_height / 2;
    CHECK_GE(pad_needed_height, 0);
    *pad_bootom = pad_needed_height - *pad_top;
    const int pad_needed_width = (*new_width - 1) * col_stride + filter_width - in_width;
    *pad_left = pad_needed_width / 2;
    CHECK_GE(pad_needed_width, 0);
    *pad_right = pad_needed_width - *pad_left;
    break;

现在我们假设输入是5 x 5，卷积核大小为3 x 3，步长为1, 1来解释上面这段代码。

最开始的这段代码的作用就是先求出新的高宽，这里是求中心卷积的大小（row_stride、col_stride为高和宽的移动步数，详细在stride章节解释）

*new_height = ceil(in_height / static_cast(row_stride));
*new_width = ceil(in_width / static_cast(col_stride));

带入实数就是：

new_width  = 5 / 1 = 5
new_height  = 5 / 1 = 5

所以这里的new_height和new_width = 5，这里会发现尺寸没有变是因为还没有把卷积核大小带进来

*new_height = ceil(in_height / static_cast(row_stride));
*new_width = ceil(in_width / static_cast(col_stride));

这一段代码会形成这样的卷积矩阵：

然后就是求要扩充上下方向的padding大小，这里会代入卷积核的大小，首先求上下

const int pad_needed_height = (*new_height - 1) * row_stride + filter_height - in_height;
*pad_top = pad_needed_height / 2;
CHECK_GE(pad_needed_height, 0);
*pad_bootom = pad_needed_height - *pad_top;

代入实数就是：

pad_needed_height = (5 - 1) * 1 + 3 - 5 = 2
pad_top = 2 / 2 = 1
pad_bootom = 2 - 1 = 1

所以上下两个方向填充1的padding大小，此时卷积矩阵如下：

然后就是求它的左右两个方向要填充的padding大小：

const int pad_needed_width = (*new_width - 1) * col_stride + filter_width - in_width;
*pad_left = pad_needed_width / 2;
CHECK_GE(pad_needed_width, 0);
*pad_right = pad_needed_width - *pad_left;

代入实数计算如下

pad_needed_width  =  (5 - 1) * 1 + 3 - 5 = 2
pad_left = 2 / 2 = 1
pad_right = 2 - 1 = 1

        所以左右方向填充1的padding大小，通过上面的code可以看出来填充的大小和你的卷积核大小是有关联的，卷积核越大，填充的padding就越大，这会导致卷积量也变大，所以合理的选择一个卷积核的大小也是很关键的，这里顺便从代码角度解释一下为什么常用的是奇数，这里把卷积核尺寸换成偶数（3换成4）看下结果：

pad_needed_width  =  (5 - 1) * 1 + 4 - 5 = 3
pad_left = 3 / 2 = 1.5
pad_right = 1.5 - 1 = 0.5

        可以看到得到的结果出现了小数点，导致左右两个值不对成了，那么分配的结果也就不对了，不过现代的cnn内置的神经网络算法可以忽略这个问题，只不过内部会进行更多的运算来纠正这个问题，这样就会导致计算量增加，最后矩阵就是下图这样： 

 

        以上就是same对左右上下填充的方式，它是先填充上下，在填充左右，这样就保证了高度的一致性，最终从5 x 5变成了7 x 7，边缘扩充的数据都为0，只有中心的5 x 5部位是原始数。

        上下两个维度填充的数据和原始维度保持一致，左右填充时维度大小和H一致。

3.2.2 valid

        valid就最好理解了，只有卷积核完全与输入数据交汇时才会进行卷积，这种计算量最少，同时它不会进行填充，所以valid输出的尺寸会变小，同时valid有一个坏处，若输入尺寸不满足卷积核要求，则不会进行卷积，例如输入尺寸是5 x 5，卷积核大小是5 x 5，那么输出大小就是1 x 1，若卷积核大小为10 x 10由于不会边缘填充valid会舍弃卷积，导致输出为0 x 0，提取不到任何特征，同时也会出现丢失信息的情况：例如输入5 x 5，卷积核大小为3 x 3，输出大小为3 x 3，会导致一些不满足卷积条件的数据被舍弃掉，这是因为Vilid的锚点以左上角为锚点，只有左上角与输入数据完全交汇重叠才会进行卷积：

 

下面是它的输出矩阵的C实现：

case Padding::VALID:
    *new_height = ceil((in_height - filter_height + 1.f) / static_cast(row_stride));
    *new_width = ceil((in_width - filter_width + 1.f) / static_cast(col_stride));
    *pad_top = 0;
    *pad_bottom = 0;
    *pad_left = 0;
    *pad_right = 0;

这里只是计算了一下新的输出尺寸，其公式是：H/Wout = (H/Win - KH/W + 1) / R/Cs。

可以看到它并没有进行填充，pad参数一律设置为0。

3.2.3 full

        full模式一般在神经网络算法里没有实现，这个模式与same类似，都是边缘填充，唯一不同的区别就是卷积时full以右下角为锚点，只有右下角的锚点与输入数据交汇时开始卷积，这也就意味着输出的尺寸可能会更大，并且会进行更多的计算。

动图如下：

3.3 卷积核算子（operator）

首先看一张图：

 

通过这个图可以看到每次卷积时都会将卷积到的元素值依次与中间的卷积核算子进行一次加权计算，然后在输入到输出矩阵里：

可以把卷积核算子理解为加权数组，每次卷积的元素都会和卷积核里的元素进行一次相乘并相加输出到输出矩阵里，这么做的目的是为了增强特征，卷积核里的数据也叫卷积算子，它是根据观测输入图像的数据来进行计算的，卷积算子常用的有如下几种：

3.3.1 Robert 算子

Robert算子，又称Roberts边缘检测算子，是一种利用局部差分算子寻找边缘的算子。

3.3.2 Prewitt算子

Prewitt算子是一种一阶微分算子的边缘检测,利用像素点上下、左右邻点的灰度差,在边缘处达到极值检测边缘,去掉部分伪边缘,对噪声具有平滑作用。

3.3.3 Sobel 算子

Sobel算子是一种常用的边缘检测算法，是一种离散性差分算子，用差分近似代替梯度。对x求1阶差分用来检测竖直边缘，同样的对y求1阶差分用来检测水平边缘，它是对Prewitt算子的一种优化.

3.3.4 Laplance 算子

在二阶导数的时候,最大变化处的值为零即边缘是零值，通过二阶导数计算边缘。

---

        通过卷积算子提取边缘加权值，来对卷积后的值进行一次加权然后输出到卷积矩阵里，可以说卷积是对提取的特征在进行一次增强来保证提取特征的准确性，尤其是在图像上会更加有效，因为不同的卷积算子可以起到颜色增强、边缘提取的作用，例如上面提到的填充方式，在最初难免会出现提取到0的情况，这样就会导致部分边缘颜色为0，通过算子增强可以弥补这个问题。

3.4 卷积核深度与个数（depth、filter）

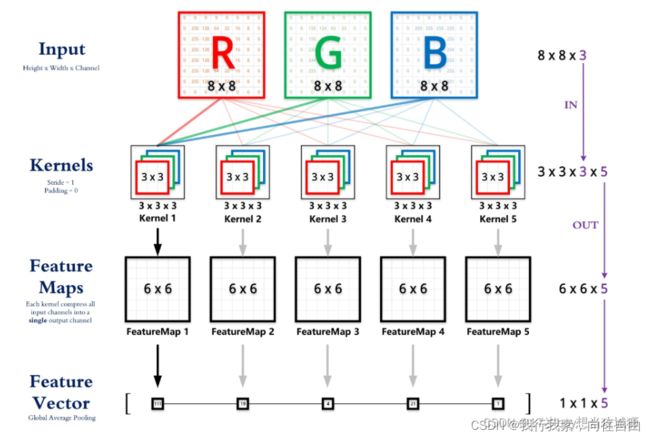
卷积核深度与输入数据的通道有关，例如一副RGB真彩图的尺寸维度是8 x 8 x 3，分别对应高度、宽度、通道数，其中通道数是与卷积核深度对应的：

通过上图可以看到卷积核是3 x 3的，但是可以看到每组卷积核算子有三层，RGB分别对这三层做一次加权计算，所以卷积在对多通道做深度提取时是这样的：

首先提取R通道与卷积核算子进行运算，这里有一点需要注意，卷积核算子里的值也是通过不同通道的值来取的 

 那么依次类推G、B也是如此：

这代表卷积每次提取时都是按通道提取的：

卷积核个数代表输出的维度，在上图中我们可以看到卷积核算子有5组，每组有3个卷积核算子，这里的5组就对应了卷积核个数，这里接上图： 

通过这张完整的图我们可以看到它在进行卷积之后输出的6 x 6是特征尺寸，输出5组特征尺寸，最后会将这五组特征尺寸输入到一个1 x 1 x 5的向量里，也就意味着无论你的通道是多少，RGB或者RGBA或者灰度图，最总都会变成一个1 x 1的向量维度，卷积核个数越多也就意味着提取的信息就越多，特征就越多，但也意味着卷积层会越大。

3.5 步长（strides）

步长是卷积里最容易理解的一个参数，它代表着卷积每次挪移的长度，比如把输入理解成一个格子，移动的格子数就是卷积的步长，下图是一个步数为1的卷积过程：

下图是步长为2的移动动图：

还有一种就是我们通常搭建卷积层的时会看见这样的写法：

keras.layers.Conv2D(18, (3, 3), strides = (2, 2), padding="same")

strides分别有两个整数组成：row_stride、col_stride，分别对应行、高。

通常情况下strides给的是1，这样的赋值是：1, 1（row_stride/col_stride）

keras.layers.Conv2D(18, (3, 3), strides = 1, padding="same")

4.搭建卷积层

这里用keras作为演示，下列代码演示了使用keras搭建了一个Sequential模型的第一层，卷积层：

格式如下：

输入层：5 x 5 x 1

卷积层：3 x 3 x 8 x 1，pandding：same

import tensorflow as tf
from tensorflow import keras
 
model = keras.Sequential()
model.add(keras.layers.Input(shape = (5, 5, 1)))
model.add(keras.layers.Conv2D(filters = 8, kernel_size = (3, 3), strides = 1, padding = "same"))
model.summary()

输出：

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 conv2d (Conv2D)             (None, 5, 5, 8)           80        
                                                                 
=================================================================
Total params: 80
Trainable params: 80
Non-trainable params: 0
_________________________________________________________________

在换一个场景，假设输入层是56 x 56 x 3图像数据，那么我们根据这个输入层来设计我们的卷积层。

1. 首先根据输入是图像数据，所以我们要尽可能的将图像数据保留下来，所以使用same进行填充卷积方式，保证边缘能够被有效的提取到：padding：same

2. 根据输入是图像56 x 56、那么又得知了padding方式是same，所以我们可以进行一次计算：

代入之前计算same的公式就可以了：

计算3 * 3：

上下为1

(56 - 1) * 1 + 3 - 56) = 2
top = 2 / 2 = 1
pad_bootom = 2 - 1 = 1

左右和上下公式一样，所以这里直接给出得数左右也是填充1行，然后56 x 56变成了58 x 58。

然后计算58 x 58 / 3 x 3 = 373.77，所以3 x 3的卷积过程大约需要373次，但是出现了小数，说明这样的padding可能会导致丢失数据。

那么计算7 x 7的：

(56 - 1) * 1 + 7 - 56) = 6
top = 6 / 2 = 3
pad_bootom = 6 - 3 = 3

左右也是一样，padding大小都为3。

然后填充之后大小为62 x 62 (56 x 3 + 56 x 3 + 62 x 3 + 62 x 3)。

然后在计算62 x 62 / 7 x 7 = 78.44。

7 x 7大约需要78次，但是也出现了小数，虽然卷积次数变少了，但是可能会丢失特征，并不能保证完整的特征性。

所以在计算5 x 5：

(56 - 1) * 1 + 5 - 56) = 4
top = 4 / 2 = 2
pad_bootom = 4 - 2 = 2

左右依然一样，都是2组，填充之后的大小就是（上：56 x 2 + 下：56 x 2 + 左60 x 2 + 右 60 x 2） = 60 x 60。

然后计算 60 x 60 / 5 x 5 = 144。

这次没有了小数，说明5 x 5的卷积核大小可以完整的卷积所有的特征，因此得到卷积核大小为5 x 5。

最后filters在处理图像时给8是最合适的，这是许多神经网络开发者在经过无数次调参给出的最合适的处理多通道时特征提取最完美的值，因为filters越多卷积的次数会增加，可能会出现重复特征，会拉跨神经网络造成过拟合的问题，同时yolo里使用的filters也是8。

所以最后我们得到下面最适合我们的卷积层：

import tensorflow as tf
from tensorflow import keras
 
model = keras.Sequential()
model.add(keras.layers.Input(shape = (56, 56, 3)))
model.add(keras.layers.Conv2D(filters = 8, kernel_size = (7, 7), strides = (1, 1), padding = "same"))
model.summary()

这些参数都需要自己去代入分析计算，一步一步调整出来，如果想自己调整出来需要明白卷积这些是如何工作的，调出最时候自己当前应用场景的神经网络。