K-means及其改进
一. k-means
1.算法流程
给定数据样本集 D = { x 1 , x 2 , . . . , x m } D=\{x_1,x_2,...,x_m\} D={x1,x2,...,xm},k-means欲将 D D D划分成K个簇 C = { c 1 , c 2 , . . . , c k } C=\{c_1,c_2,...,c_k\} C={c1,c2,...,ck}并且簇之间没有交集。其目标是最小化平方误差和:
E = ∑ i = 1 k ∑ x ∈ c i ∣ ∣ x − u i ∣ ∣ 2 2 \begin{aligned} E=\sum_{i=1}^k\sum_{x\in c_i}||x-u_i||_{2}^2 \end{aligned} E=i=1∑kx∈ci∑∣∣x−ui∣∣22
其中 u i = 1 ∣ c i ∣ ∑ x ∈ c i x u_i=\cfrac{1}{|c_i|}\sum_{x\in c_i}x ui=∣ci∣1∑x∈cix是簇 c i c_i ci的均值向量(簇的形心)。从几何上理解就是k-means划分的每个簇中的样本都紧紧地挨着簇的形心。想要最小化平方误差和并不容易,找到它的最优解需要考虑所有可能的簇的划分,这是个NP难问题。所以,k-means采用了贪心的策略,通过迭代来找到局部最优解。算法流程如下:
- 输入数据集D,簇的个数k
- 从D中随机选择k个不同的样本作为初始均值向量{ u 1 , u 2 , . . . , u k u_1,u_2,...,u_k u1,u2,...,uk}
- REPEAT
- 初始化k个簇为空 c i = ∅ c_i=\varnothing ci=∅
- for i i i 1 to m :
- 分别计算 x i x_i xi到k个均值向量的距离: d i j = d i s t ( x i , u j ) , j = 1 , 2 , . . . , k d_{ij}=dist(x_i,u_j),j=1,2,...,k dij=dist(xi,uj),j=1,2,...,k
- 找到与 x i x_{i} xi距离最近的均值向量对应的标号: j ∗ = m i n j ∈ [ 1 , k ] d i j j^*= min_{j \in [1,k]}\enspace d_{ij} j∗=minj∈[1,k]dij
- 将 x i x_i xi添加到对应簇中: c j ∗ = c j ∗ ∪ x i c_{j^*}=c_{j^*} \cup x_i cj∗=cj∗∪xi
- end for
- for i i i 1 to k:
- 更新均值向量: u i = 1 ∣ c i ∣ ∑ x ∈ c i x u_i =\cfrac{1}{|c_i|}\sum_{x\in c_i}x ui=∣ci∣1∑x∈cix
- end for
- UNTIL:所有均值向量收敛,即变化极小
- 输出: C = { c 1 , c 2 , . . . , c k } C=\{c_1,c_2,...,c_k\} C={c1,c2,...,ck}
2.代码实现
python原生实现代码如下:
def kmeans(data,k):
m,n = data.shape
#不重复随机抽样,产生k个不同的整数
r = random.sample(range(0,m),k)
#初始化均值向量
u= data[r]
#初始化K个簇
clusters =[]
for i in range(0,k):
clusters.append([])
#迭代至均值向量收敛
while True:
#遍历所有样本,划分簇
for i in range(0,m):
min = 0
index = -1
#找到样本最近的中心
for j in range(0,k):
dist = math.sqrt((data[i]-u[j]) @ (data[i]-u[j]).T)#计算距离
if(j == 0):
min = dist
index =j
continue
if(dist < min):
min = dist
index = j
#样本加入对应簇
clusters[index].append(data[i].tolist())
#更新均值
u_old = u.copy()
for i in range(0,k):
c = np.array(clusters[i])
for j in range(0,n):
u[i][j] = c[:,j].mean()
#判断收敛
delta = (u-u_old) @(u-u_old).T
if np.all(delta < 1e-6):break
else: #继续迭代,更新簇
clusters.clear()#清空
for i in range(0,k):
clusters.append([])
return clusters
k-means算法的时间复杂度是O(mks),m是数据量,k是聚类簇的个数,s是迭代次数。k-means收敛的较快,适用于大规模数据。
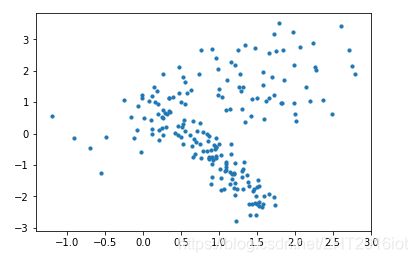
现在产生一个随机数据集:
X=datasets.make_classification(n_samples=200,
n_features=2,
n_informative=2,
n_redundant=0,
n_repeated=0,
n_clusters_per_class=1)[0]
plt.scatter(X[:,0], X[:,1],marker='o',s=10)
plt.show()
3.K-means缺点
- K值要人为给出,需要有先验知识
- 聚类结果依赖于初始聚类中心的随机选择,可能收敛到局部最优解,而非全局最优
- 受噪声和离群点的影响极大
二 K-means++
该算法对K-means做了改进,优化了初始聚类中心的随机选择,使其能够收敛于全局最优解。
1.算法流程
主要是初始化聚类中心的流程,其余的流程和K-means一样。
- 随机选择一个样本做第一个聚类中心
- 第n个中心的选择与前n-1个中心有关:
- 计算所有样本到当前已有中心的距离和,选择距离和最大的样本作为新的聚类中心
- 直到K个中心选择完
这个流程的思想就是想让初始化的聚类中心尽可能散得开一些。
2.代码实现
def initCenters(data,k):
m,n = data.shape
centers = np.zeros((k,n))
#随机选择第一个聚类中心
first = np.random.randint(0,m)
centers[0] =data[first,:]
for t in range(1,k):
c_size =t
maxs = 0
index = -1
#遍历所有样本,找到最远点
for i in range(0,m):
sums = 0.0
for j in range(0,c_size):
sums +=math.sqrt((data[i,:]-centers[j,:]) @ (data[i,:]-centers[j,:]).T)
if sums > maxs:
maxs = sums
index = i
#加入一个聚类中心
centers[t] = data[index,:]
return centers
def kmeansPlus(data,k):
m,n = data.shape
#初始化均值向量
u= initCenters(data,k)
#初始化K个簇
clusters =[]
for i in range(0,k):
clusters.append([])
#迭代至均值向量收敛
while True:
#遍历所有样本,划分簇
for i in range(0,m):
min = 0
index = -1
#找到样本最近的中心
for j in range(0,k):
dist = math.sqrt((data[i]-u[j]) @ (data[i]-u[j]).T)#计算距离
if(j == 0):
min = dist
index =j
continue
if(dist < min):
min = dist
index = j
#样本加入对应簇
clusters[index].append(data[i].tolist())
#更新均值
u_old = u.copy()
for i in range(0,k):
c = np.array(clusters[i])
for j in range(0,n):
u[i][j] = c[:,j].mean()
#判断收敛
delta = (u-u_old) @(u-u_old).T
if np.all(delta < 1e-6):break
else: #继续迭代,更新簇
clusters.clear()#清空
for i in range(0,k):
clusters.append([])
return clusters
现在生成一个数据集,比较一下K-means和K-means++的聚类效果:
def showClusters(c1,c2,c3):
plt.scatter(c1[:,0],c1[:,1],c='r',s=10)
plt.scatter(c2[:,0],c2[:,1],c='b',s=10)
plt.scatter(c3[:,0],c3[:,1],c='g',s=10)
plt.scatter(c1[:,0].mean(),c1[:,1].mean(),marker='*',c=[[0,0,0]],s=50)
plt.scatter(c2[:,0].mean(),c2[:,1].mean(),marker='*',c=[[0,0,0]],s=50)
plt.scatter(c3[:,0].mean(),c3[:,1].mean(),marker='*',c=[[0,0,0]],s=50)
plt.show()
X = datasets.make_moons(n_samples=100, noise=0.2, random_state=0)[0]
cls = kmeans(X,3)
c1 = np.array(cls[0])
c2 = np.array(cls[1])
c3 = np.array(cls[2])
showClusters(c1,c2,c3)
cls1 = kmeansPlus(X,3)
c1 = np.array(cls1[0])
c2 = np.array(cls1[1])
c3 = np.array(cls1[2])
showClusters(c1,c2,c3)
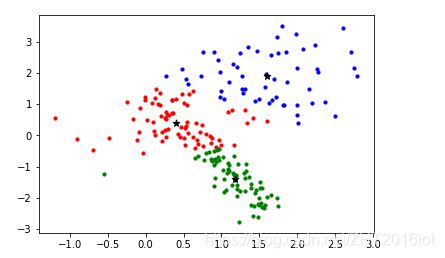
上图是K-means聚类的效果,下图是K-means++聚类的效果:
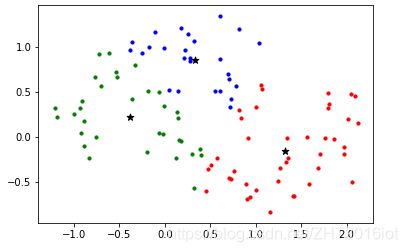
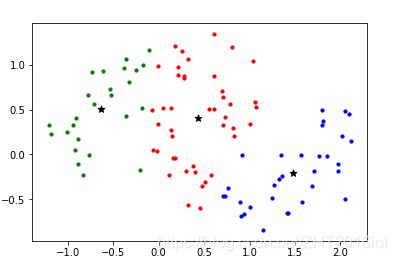
从上图可以看出,K-means簇内没有那么紧凑,K-means++划分的簇内更紧凑。说明K-means只是局部收敛了,这是由于初始化中心随机选择导致的,对于这个点还有很多优化方法,例如二分K-means和最小生成树k-means,这里不再赘述。
三 K-mediods
1.算法流程
k-means最大的缺点就是受到离群点或噪声的影响极大,这是因为k-means更新中心的方式是计算簇内均值向量,离群点会极大地影响某属性列的均值,从而导致中心点偏离。k-中心点算法解决了这个问题,因为其思想是:尝试用非中心点替代中心点,若替代后总代价减小了,就进行真正替代。 如此,更新的中心点总是某样本,且用总代价衡量,中心点不会偏离簇。
算法流程如下:
- 输入:数据集D和簇的个数k
- 随机选择k个不同的样本作为原始中心点
- 初次划分k个簇
- 计算初次划分产生的总代价:e
- REPEAT
- FOR i FROM 0 TO k
- 随机选择一个非中心点去尝试替代第i个中心
- 尝试重新划分k个簇:cls_try
- 计算重新划分产生的总代价:e_try
- IF e_try - e < 0
- 进行真正的替代
- 进行真正的划分:cls = cls_try
- 替换e = e_try
- THEN :撤销尝试
- END IF
- END FOR
- UNTIL 簇没有发生任何变化
代码实现如下:
#计算总代价
def calcE(clusters,mediods):
loss = 0.0
for i in range(0,mediods.shape[0]):
for x in clusters[i]:
loss+=math.sqrt((x-mediods[i]) @ (x-mediods[i]).T)
return loss
#划分簇
def clustersPartition(data,mediods):
#初始化k个空簇
clusters =[]
for i in range(0,mediods.shape[0]):
clusters.append([])
#样本离那个中心近就划分到对应簇
for j in range(0,data.shape[0]):
mini = float('inf')
index = -1
for i in range(0,mediods.shape[0]):
dist = math.sqrt((data[j]-mediods[i]) @ (data[j]-mediods[i]).T)
if(dist<mini):
mini = dist
index = i
clusters[index].append(data[j].tolist())
for i in range(0,mediods.shape[0]):
clusters[i] = np.array(clusters[i])
return clusters
#随机挑选一个非中心对象
def selectRandom(data,mediods):
m = data.shape[0]
i = np.random.randint(0,m)
while i>=m and data[i] in mediods:
i = random.randint(0,m)
return data[i]
#k-中心点算法
def kmediods(data,k):
m,n = data.shape
#产生k个不同的随机数
r = random.sample(range(0,m),k)
#初始化k个中心点
mediods = data[r]
#产生k个簇
clusters = clustersPartition(data,mediods)
#计算当前总代价
e = calcE(clusters,mediods)
#迭代次数和最大迭代次数
iters = 0
maxIters = m
while iters<maxIters:
changed = 0
#尝试替换每个中心
for i in range(0,k):
centerOld = mediods[i].copy()
centerNew = selectRandom(data,mediods)#随机选择一个非中心点
mediods[i] = centerNew#用非中心点尝试更新中心
clusters_try = clustersPartition(data,mediods)#尝试划分新的簇
e_try = calcE(clusters,mediods)#计算更新后的损失
#若总代价在减小
if(e_try - e) < 0:
clusters.clear()
clusters = clusters_try#更新簇
e = e_try
changed+=1#替代次数
else:
mediods[i] = centerOld#撤销尝试
#若一轮过程中所有中心点都没被替换
if changed == 0:
iters+=1
return [clusters,mediods]
做一个小实验,随机产生一个带离群点的数据集,分别对其用k-mediods和k-means进行聚类,观察离群点对两种算法的影响:
def showClusters(c1,c2,c3,centers):
plt.scatter(c1[:,0],c1[:,1],c='r',s=10)
plt.scatter(c2[:,0],c2[:,1],c='b',s=10)
plt.scatter(c3[:,0],c3[:,1],c='g',s=10)
plt.scatter(centers[:,0],centers[:,1],marker='*',c=[[0,0,0]],s=50)
plt.show()
moids = [[2,2],[8,2],[0,8]]
X = datasets.make_blobs(n_samples=100, n_features=2, centers=moids,cluster_std=1)[0]
X = np.append(X,[[10,10]],axis=0)#离群点
cls,centers= kmediods(X,3)
print(calcE(cls,centers))
c1 = cls[0]
c2 = cls[1]
c3 = cls[2]
showClusters(c1,c2,c3,centers)
cls1,centers1 = kmeans(X,3)
print(calcE(cls1,centers1))
c11 = cls1[0]
c21 = cls1[1]
c31 = cls1[2]
showClusters(c11,c21,c31,centers1)
下图分别是k-mediods和k-means的聚类后的总代价以及结果:
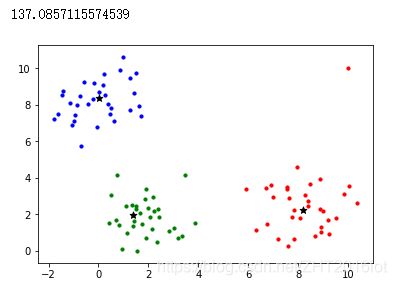
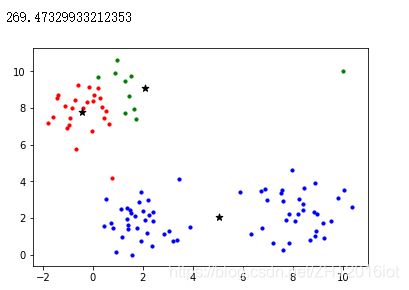
可以观察到k-means受到离群点的影响,聚类中心严重偏离了簇内样本。但是,并不是说k-mediods一定比k-means好。实际上,k-mediods的时间复杂度比k-means高出许多,只适用于小规模数据,而k-means在大规模数据上的聚类效率高出许多。