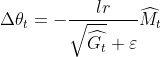优化器模块

一、梯度下降法

       梯度下降法根是最基本的优化算法。根据在训练过程中每次迭代使用数据量的大小(一次iter计算的loss使用到的数据量的大小)，可以将梯度下降法分成批梯度下降法(Batch Gradient Descent，BGD)、随机梯度下降法(Stochastic Gradient Descent,SGD)和小批量梯度下降(Mini-Batch Gradient Descent ,MBGD)

1.Batch Gradient Descent，BGD

(1)梯度更新规则:

BGD 采用整个训练集的数据来计算loss对参数的梯度：

(2)公式

                              

表示时刻t时的参数值， 表示t时刻时计算出的待更新的参数的梯度。

(3)代码

for i in range(nb_epochs):
  params_grad = evaluate_gradient(loss_function, data, params)
  params = params - learning_rate * params_grad

先定义迭代次数 epoch，计算梯度向量 params_grad，然后沿着梯度的方向更新参数 params，learning rate 决定了我们每一步迈多大。

(4)缺点

由于这种方法是在一次更新中，就对整个数据集计算梯度，所以计算起来非常慢，遇到很大量的数据集也会非常棘手，而且不能投入新数据实时更新模型。

2.Stochastic Gradient Descent (SGD)

(1)梯度更新规则:

BGD 使用一个样本的loss对参数的梯度。

(2)公式

                     

              表示时刻t时的参数值， 表示t时刻时计算出的待更新的参数的梯度。

(3)代码

for i in range(nb_epochs):
  np.random.shuffle(data)
  for example in data:
    params_grad = evaluate_gradient(loss_function, example, params)
    params = params - learning_rate * params_grad

(4)优缺点

优点：优化快，对于很大的数据集来说，可能会有相似的样本，这样 BGD 在计算梯度时会出现冗余，而 SGD 一次只进行一次更新，就没有冗余，而且比较快，并且可以新增样本。

缺点：SGD使用一个样本优化参数，

          a)使得SGD并不是每次迭代都向着整体最优化方向。所以虽然训练速度快，但是准确度下降，并不是全局最优。虽然包含一定的随机性，但是从期望上来看，它是等于正确的导数的。

         b)更新比较频繁，会造成 loss function 有严重的震荡。BGD 可以收敛到局部极小值，当然 SGD 的震荡可能会跳到更好的局部极小值处。

3.Mini-Batch Gradient Descent(MBGD)

(1)梯度更新规则：

MBGD 每一次利用一小批样本，即 n 个样本进行计算，这样它可以降低参数更新时的方差，收敛更稳定，另一方面可以充分地利用深度学习库中高度优化的矩阵操作来进行更有效的梯度计算。

(2)公式

                                      

 表示时刻t时的参数值， 表示t时刻时计算出的待更新的参数的梯度。           

  参数更新差值：

                                      

          由此可以看出，影响MSGD的主要因素有：batch_size，学习率，梯度估计。

(3)代码

和 SGD 的区别是每一次循环不是作用于每个样本，而是具有 n 个样本的批次

for i in range(nb_epochs):
  np.random.shuffle(data)
  for batch in get_batches(data, batch_size=50):
    params_grad = evaluate_gradient(loss_function, batch, params)
    params = params - learning_rate * params_grad

（4）优缺点

优点：一次使用n个数据，可以降低参数更新时的方差，收敛更稳定，另一方面可以充分地利用深度学习库中高度优化的矩阵操作来进行更有效的梯度计算。

缺点：a)不能保证很好的收敛性，learning rate 如果选择的太小，收敛速度会很慢，如果太大，loss function 就会在极小值处不停地震荡甚至偏离。

           b)对于非凸函数，还要避免陷于局部极小值处，或者鞍点处，因为鞍点周围的error是一样的，所有维度的梯度都接近于0，SGD 很容易被困在这里。（会在鞍点或者局部最小点震荡跳动，因为在此点处，如果是训练集全集带入即BGD，则优化会停止不动，如果是mini-batch或者SGD，每次找到的梯度都是不同的，就会发生震荡，来回跳动。

二、梯度下降法的改进

为了更有效的训练神经网络，在MBGD的基础上使用一些改进方法。改进方法有两个方向：一个是学习率衰减方向—对参数更新的步数大小做调整，一个是梯度估计修正方向—对参数的更新方向做调整。

 学习衰减方向

1.Adaptive Gradient Algorithm(AdaGrad)算法

(1) 原理：每次迭代时自适应地调整每个参数的学习率。在第t次迭代时，先计算每个参数梯度平方 的累计值。

 (2)公式               

             首先计算每个参数梯度平方的累计值

                                  

参数更新差值为：

                 

是为了避免分母是0而取得非常小的常数，一般取值到。

(3)代码

(4)作用：

在该算法中，如果某个参数的偏导数累计比较大，其学习率相对较小；相反，如果其偏导数累计较小，其学习率相对较大。但整体是随着迭代次数的增加，学习率变小。

(5)优缺点：

缺点：经过一定次数的迭代依旧没有找到最优点时，由于学习率已经非常小了，很难再继续找到最优点。

2.RMSprop算法

(1)原理：一种自适应学习率方法，可以在有些情况下避免AdaGrad算法中学习率不断单调下降以至于过早衰减的缺点。

(2)公式

首先计算每次迭代梯度平方的指数衰减移动平均。 

                    

为衰减率，一般取0.9。

参数更新差值为：

                    

(3)代码

(4)优缺点

RMSprop和AdaGrad的区别在于的计算由累积方式变成了指数衰减移动平均。在迭代过程中，每个参数的学习率并不是呈衰减趋势，既可以变大也可以变小。

Momentum算法：在梯度衰减方向上进行改进

SGD方法的一个缺点是其更新方向完全依赖于当前batch计算出的梯度，因而十分不稳定。

(1)Momentum算法的原理：使用之前累积动量来代替真正的梯度，每次迭代的梯度可以看做加速。该算法在梯度下降法的梯度衰减方向做改进，通过梯度的指数移动平均(累积的之前的梯度值)来代替每次的实际梯度，缓解梯度震荡，加速学习。当接近最优值时梯度会比较小，由于学习率固定，普通的梯度下降法的收敛速度会变慢，有时甚至陷入局部最优。这时如果考虑历史梯度，将会引导参数朝着最优值更快收敛，这就是动量算法的基本思想。

                                         

           表示动量因子，通常取0.9，表示学习率

(2)作用

     每个参数的实际更新差值取决于最近一段时间内梯度的加权平均值。当某个参数在一段时间内的梯度方向不一致时，其真实的参数更新幅度变小；相反，当某个参数在一段时间内的梯度方向一致时，其真实的参数更新幅度变大，起到加速作用。一般而言，在迭代初期，梯度方向都比较一致，动量法起到加速作用，可以更快地到达最优点；在迭代后期，梯度方向会不一致，在收敛值附近震荡，东良方会起到减速的作用，增加稳定性。

指数移动平均:ema

(1)指数移动平均：又称指数加权移动平均值，即根据各个元素所占权重计算平均值。指数加权移动平均中的“指数”表示每个元素所占权重成指数分布。

  假设有n个权重数据： ,ema的计算公式：

                                                                 

其中成为影子权重。

当越大时，滑动平均得到的值越和的历史值相关。

使用到ema思路的优化器

1.SGD+Momentum

   SGD公式：         

                          

   SGD+Momentum 是在SGD的基础上增加 Momentum，公式：

                      

                         

optimizer = torch.optim.SGD(model.parameters(), args.lr,
                            momentum=args.momentum,
                            weight_decay=args.weight_decay)

2.Adam算法

(1)原理                                       

    可以看做动量法和RMSprop算法的结合，不但使用动量作为参数更新方向，而且可以自适应调整学习率。

(2)公式

计算梯度的指数加权平均(和动量法类似)         

                 

计算梯度平方的指数加权平均(和RMSprop算法类似)

                  

其中和分别为两个移动平均的衰减率，通常=0.9，=0.99

偏差矫正

当,时，在迭代初期，和的值会比真实值小，特别是当和接近于1时，因此要对偏差进行矫正。

对偏差进行修正

                            

                            

 

Adam算法的参数更新差值为

                               

（4）代码

def adam(params: List[Tensor],grads: List[Tensor],exp_avgs: List[Tensor],
exp_avg_sqs: List[Tensor], max_exp_avg_sqs: List[Tensor],state_steps: List[int],
amsgrad: bool,beta1: float,beta2: float,lr: float,weight_decay: float,eps: float):
   
    for i, param in enumerate(params):

        grad = grads[i]
        exp_avg = exp_avgs[i]
        exp_avg_sq = exp_avg_sqs[i]
        step = state_steps[i]
        if amsgrad:
            max_exp_avg_sq = max_exp_avg_sqs[i]

        bias_correction1 = 1 - beta1 ** step
        bias_correction2 = 1 - beta2 ** step

        if weight_decay != 0:
            grad = grad.add(param, alpha=weight_decay)

        # Decay the first and second moment running average coefficient
        exp_avg.mul_(beta1).add_(grad, alpha=1 - beta1)
        exp_avg_sq.mul_(beta2).addcmul_(grad, grad, value=1 - beta2)
        if amsgrad:
            # Maintains the maximum of all 2nd moment running avg. till now
            torch.maximum(max_exp_avg_sq, exp_avg_sq, out=max_exp_avg_sq)
            # Use the max. for normalizing running avg. of gradient
            denom = (max_exp_avg_sq.sqrt() / math.sqrt(bias_correction2)).add_(eps)
        else:
            denom = (exp_avg_sq.sqrt() / math.sqrt(bias_correction2)).add_(eps)

        step_size = lr / bias_correction1

        param.addcdiv_(exp_avg, denom, value=-step_size)

如果使用 weight_decay 的话，那么相当于目标函数加上 ,是weight_decay。所以相当于梯度要再加上  ，故使用了 grad = grad.add(p, alpha=group['weight_decay'])。

3.AdamW

AdamW是在Adam+L2正则化的基础上进行改进的算法。

        for group in self.param_groups:
            for p in group['params']:
                if p.grad is None:
                    continue

                # Perform stepweight decay
                p.mul_(1 - group['lr'] * group['weight_decay'])

                # Perform optimization step
                grad = p.grad
                if grad.is_sparse:
                    raise RuntimeError('AdamW does not support sparse gradients')
                amsgrad = group['amsgrad']

                state = self.state[p]

                # State initialization
                if len(state) == 0:
                    state['step'] = 0
                    # Exponential moving average of gradient values
                    state['exp_avg'] = torch.zeros_like(p, memory_format=torch.preserve_format)
                    # Exponential moving average of squared gradient values
                    state['exp_avg_sq'] = torch.zeros_like(p, memory_format=torch.preserve_format)
                    if amsgrad:
                        # Maintains max of all exp. moving avg. of sq. grad. values
                        state['max_exp_avg_sq'] = torch.zeros_like(p, memory_format=torch.preserve_format)

                exp_avg, exp_avg_sq = state['exp_avg'], state['exp_avg_sq']
                if amsgrad:
                    max_exp_avg_sq = state['max_exp_avg_sq']
                beta1, beta2 = group['betas']

                state['step'] += 1
                bias_correction1 = 1 - beta1 ** state['step']
                bias_correction2 = 1 - beta2 ** state['step']

                # Decay the first and second moment running average coefficient
                exp_avg.mul_(beta1).add_(grad, alpha=1 - beta1)
                exp_avg_sq.mul_(beta2).addcmul_(grad, grad, value=1 - beta2)
                if amsgrad:
                    # Maintains the maximum of all 2nd moment running avg. till now
                    torch.maximum(max_exp_avg_sq, exp_avg_sq, out=max_exp_avg_sq)
                    # Use the max. for normalizing running avg. of gradient
                    denom = (max_exp_avg_sq.sqrt() / math.sqrt(bias_correction2)).add_(group['eps'])
                else:
                    denom = (exp_avg_sq.sqrt() / math.sqrt(bias_correction2)).add_(group['eps'])

                step_size = group['lr'] / bias_correction1

                p.addcdiv_(exp_avg, denom, value=-step_size)