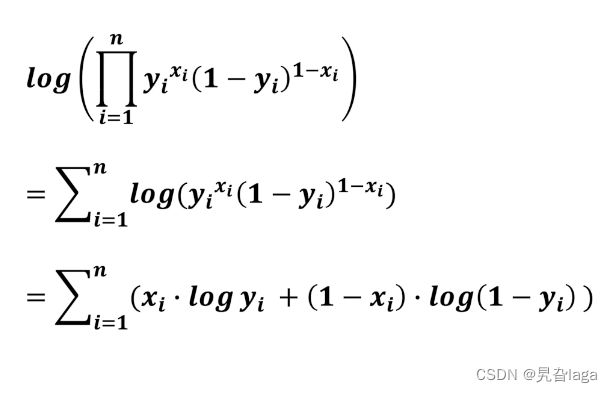逻辑回归笔记

前置知识条件

最小二乘法：两个模型之间的差别有多少，他们相差平方的最小值

 极大似然估计法：用来求两个模拟和现实最接近的最大值的情况

 交叉熵：一个模型在另一个模型基准上的差别

逻辑回归

1.分类和回归任务的区别

  我们可以按照任务的种类,将任务分为回归任务和分类任务.那这两者的区别是什么呢?按照较官方些的说法,输入变量与输出变量均为连续变量的预测问题是回归问题,输出变量为有限个离散变量的预测问题成为分类问题.

        通俗一点讲,我们要预测的结果是一个数,比如要通过一个人的饮食预测一个人的体重,体重的值可以有无限多个,有的人50kg,有的人51kg,在50和51之间也有无限多个数.这种预测结果是某一个确定数,而具体是哪个数有无限多种可能的问题,我们会训练出一个模型,传入参数后得到这个确定的数,这类问题我们称为回归问题.预测的这个变量(体重)因为有无限多种可能,在数轴上是连续的,所以我们称这种变量为连续变量.

        我们要预测一个人身体健康或者不健康,预测会得癌症或者不会得癌症,预测他是水瓶座,天蝎座还是射手座,这种结果只有几个值或者多个值的问题,我们可以把每个值都当做一类,预测对象到底属于哪一类.这样的问题称为分类问题.如果一个分类问题的结果只有两个,比如"是"和"不是"两个结果,我们把结果为"是"的样例数据称为"正例",讲结果为"不是"的样例数据称为"负例",对应的,这种结果的变量称为离散型变量.
————————————————
版权声明：本文为CSDN博主「winrar_setup.rar」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_39445556/article/details/83930186

2.将回归函数带入sigmoid函数

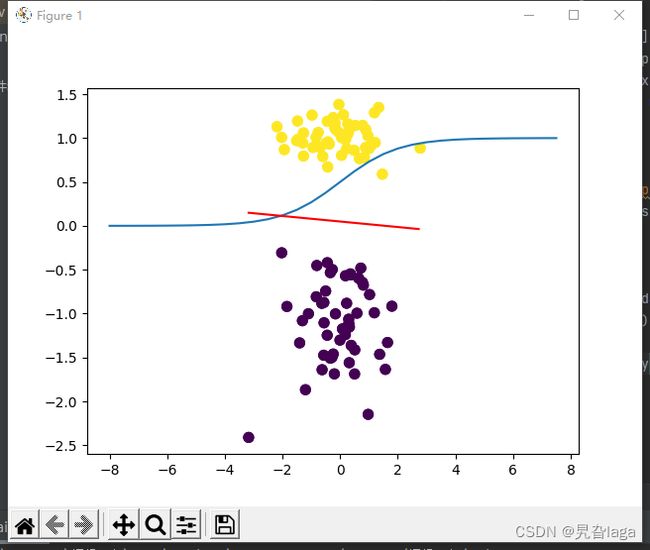
 这样输出的预测值可以控制在0到1之间

我们可以发现：

Sigmoid函数决定了模型的输出在(0,1)(0,1)区间，所以逻辑回归模型可以用作区间在(0,1)(0,1)的回归任务，也可以用作{0,1}{0,1}的二分类任务；同样，由于模型的输出在(0,1)(0,1)区间，所以逻辑回归模型的输出也可以看作这样的“概率”模型：

(=1∣)=()(=0∣)=1−()P(y=1∣x)=f(x)P(y=0∣x)=1−f(x)

所以，逻辑回归的学习目标可以通过极大似然估计求解：

，即使得观测到的当前所有样本的所属类别概率尽可能大；通过对该函数取负对数，即可得到交叉熵损失函数：

这里表示样本量，，表示特征量，，接下来的与之前推导一样，通过梯度下降求解的更新公式即可：

所以w的更新公式：

3.代码实现

import inline as inline
import numpy as np
import os
os.chdir('../')

import matplotlib.pyplot as plt
t = np.arange(-8,8,0.5)
d_t = 1 / (1 + np.exp(-t))
plt.plot(t,d_t)
import numpy as np


class LogisticRegression(object):
    # 构造函数，确定对象的一些初始值
    def __init__(self, solver='sgd',
                 eta=None, epochs=10, batch_size=16, if_standard=True, fit_intercept=True):
        # 100个数据，遍历一遍叫做一个epoch，  原来的数据0-255，归一化后0-1
        # y = w*x + b
        # [[w11,w12,b1],
        # [w21,w22,b2]]
        self.w = None
        self.solver = solver

        self.fit_intercept = fit_intercept
        self.eta = eta
        self.if_standard = if_standard
        # 训练次数
        self.epochs = epochs
        # 批量处理大小
        self.batch_size = batch_size
        # 存放损失值
        self.losses = []
        # 是不是归一化数值
        if if_standard:
            self.feature_mean = None
            self.feature_std = None

    # 初始化w的值
    # y = a_1*x1+ a_2*x2 + a_2*x3
    # [w1,w2,w3]
    def init_params(self, n_features):

        self.w = np.random.random(size=(n_features, 1))

    # 激活函数
    def sigmoid_function(self, t):

        return 1 / (1 + np.exp(-t))

    # 随机梯度下降
    def _fit_sgd(self, x, y):
        # [x1,x2],[y]
        # [x1,x2,y]
        x_y = np.c_[x, y]
        count = 0
        for i in range(self.epochs):

            np.random.shuffle(x_y)
            # 100,10,
            for index in range(x_y.shape[0] // self.batch_size):
                count += 1
                # [[1,2,3],
                # [4,5,6],
                # [7,8,9]
                # ...]
                batch_x_y = x_y[self.batch_size * index: self.batch_size * (index + 1)]
                # [w,b]
                batch_x = batch_x_y[:, :-1]
                batch_y = batch_x_y[:, -1:]

                t = batch_x.dot(self.w)
                dw = -1 * (batch_y - self.sigmoid_function(t)).T.dot(batch_x) / self.batch_size
                dw = dw.T

                self.w = self.w - self.eta * dw

                # 计算损失值集合
                cost = -1 * np.sum(np.multiply(y, np.log(self.sigmoid_function(x.dot(self.w))))) + np.multiply(1 - y,
                                                                                                               np.log(
                                                                                                                   1 - self.sigmoid_function(
                                                                                                                       x.dot(
                                                                                                                           self.w))))
                # y = 1  y_hat = 0.8  y - y_hat = loss
                # loss最小

                self.losses.append(cost)

    def fit(self, x, y):

        y = y.reshape(x.shape[0], 1)
        # 是否归一化feature
        # 数据标准化使网络更容易收敛， 更快收敛，
        if self.if_standard:
            self.feature_mean = np.mean(x, axis=0)
            self.feature_std = np.std(x, axis=0) + 1e-8
            x = (x - self.feature_mean) / self.feature_std

        # 是否训练bias
        if self.fit_intercept:
            x = np.c_[x, np.ones_like(y)]

            # 初始化参数
        self.init_params(x.shape[1])
        # 更新eta
        if self.eta is None:
            self.eta = self.batch_size / np.sqrt(x.shape[0])

        self._fit_sgd(x, y)

    # 获取系数
    def get_params(self):

        if self.fit_intercept:
            w = self.w[:-1]
            b = self.w[-1]
        else:
            w = self.w
            b = 0
        if self.if_standard:
            w = w / self.feature_std.reshape(-1, 1)
            b = b - w.T.dot(self.feature_mean.reshape(-1, 1))
        return w.reshape(-1), b

    def predict_proba(self, x):

        if self.if_standard:
            x = (x - self.feature_mean) / self.feature_std
        if self.fit_intercept:
            x = np.c_[x, np.ones(x.shape[0])]
        return self.sigmoid_function(x.dot(self.w))

    # 预测类别，默认大于0.5的为1，小于0.5的为0
    def predict(self, x):

        proba = self.predict_proba(x)
        return (proba > 0.5).astype(int)

    # 绘制前两个维度的决策边界
    def plot_decision_boundary(self, x, y):
        y = y.reshape(-1)
        weights, bias = self.get_params()
        w1 = weights[0]
        w2 = weights[1]
        bias = bias[0][0]
        x1 = np.arange(np.min(x), np.max(x), 0.1)
        x2 = -w1 / w2 * x1 - bias / w2
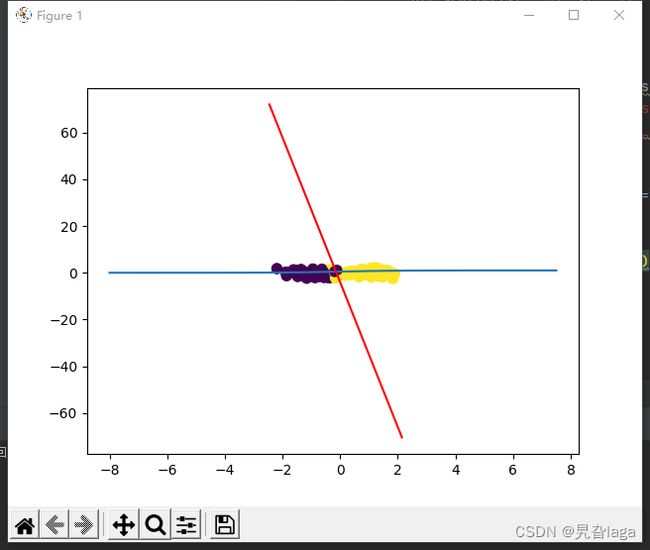
        plt.scatter(x[:, 0], x[:, 1], c=y, s=50)
        plt.plot(x1, x2, 'r')
        plt.show()

from sklearn.datasets import make_classification
data, target = make_classification(n_samples=100, n_features=2, n_classes=2, n_informative=1, n_redundant=0,
                                    n_repeated=0, n_clusters_per_class=1)
data.shape,target.shape
type(data),type(target)
plt.scatter(data[:, 0], data[:, 1], c=target,s=50)
lr = LogisticRegression()
lr.fit(data, target)
lr.plot_decision_boundary(data,target)

 

1.为什么不适用MSE作为损失函数

在logistic回归中的MSE是非凸的，如果损失函数是非凸的，我们无法保证总能找到全局最小值，相对地，我们会很可能陷入局部最小值。

2.正则化

正则化可以理解为规则化,规则就等同于一种限制。在损失函数中加入正则化项可以限制他们的拟合能力，正则化就是为了防止过拟合。