主动学习入门

1.介绍

1.1 监督学习、半监督学习、非监督学习

在机器学习(Machine learning)领域，根据是否需要样本的标签信息可分为监督学习(Supervised learning)、非监督学习(Unsupervised learning)以及半监督学习(Semi-supervised learning)：

监督学习：通过已有的一部分输入数据与输出数据之间的对应关系，生成一个函数，将输入映射到合适的输出，例如分类。例如：如果我们一开始就知道了这些数据包含的类别，并且有一部分数据(训练数据)已经标上了类标，我们通过对这些已经标好类标的数据进行归纳总结，得出一个 “数据–>类别” 的映射函数，来对剩余的数据进行分类，这就属于监督学习。

非监督学习：直接对输入数据集进行建模，例如聚类。例如：如果我们上来就对这一堆数据进行某种划分(聚类)，通过数据内在的一些属性和联系，将数据自动整理为某几类，这就属于非监督学习。

半监督学习：综合利用有类标的数据和没有类标的数据，来生成合适的分类函数。例如: 半监督学习指的是在训练数据十分稀少的情况下，通过利用一些没有类标的数据，提高学习准确率的方法。

1.2 主动学习

1.2.1 主动学习介绍

我们使用一些传统的监督学习方法做分类的时候，往往是训练样本规模越大，分类的效果就越好。但是在现实生活的很多场景中，标记样本的获取是比较困难的，这需要领域内的专家来进行人工标注，所花费的时间成本和经济成本都是很大的。而且，如果训练样本的规模过于庞大，训练的时间花费也会比较多。那么有没有办法，能够使用较少的训练样本来获得性能较好的分类器呢？主动学习(Active Learning)为我们提供了这种可能。主动学习通过一定的算法查询最有用的未标记样本，并交由专家进行标记，然后用查询到的样本训练分类模型来提高模型的精确度。
在人类的学习过程中，通常利用已有的经验来学习新的知识，又依靠获得的知识来总结和积累经验，经验与知识不断交互。同样，机器学习模拟人类学习的过程，利用已有的知识训练出模型去获取新的知识，并通过不断积累的信息去修正模型，以得到更加准确有用的新模型。不同于被动学习被动的接受知识，主动学习能够选择性地获取知识。

1.2.2 主动学习与半监督学习异同

“半监督学习和主动学习都是从未标记样例中挑选部分价值量高的样例标注后补充到已标记样例集中来提高分类器精度，降低领域专家的工作量，但二者的学习方式不同：半监督学习一般不需要人工参与，是通过具有一定分类精度的基准分类器实现对未标注样例的自动标注；而主动学习有别于半监督学习的特点之一就是需要将挑选出的高价值样例进行人工准确标注。半监督学习通过用计算机进行自动或半自动标注代替人工标注，虽然有效降低了标注代价，但其标注结果依赖于用部分已标注样例训练出的基准分类器的分类精度，因此并不能保证标注结果完全正确。相比而言，主动学习挑选样例后是人工标注，不会引入错误类标 ”。

1.2.3 主动学习流程

主动学习在统计学领域也叫查询学习、最优实验设计。“学习器”和“选择策略”是主动学习算法的2个基本且重要的模块。主动学习通过“选择策略”主动从未标注的样本集中挑选部分（1个或N个）样本让相关领域的专家进行标注；然后将标注过的样本增加到训练数据集给“学习模块”进行训练；当“学习模块”满足终止条件时即可结束程序，否则不断重复上述步骤获得更多的标注样本进行训练。此外，主动学习算法有个关键的假设：“The key hypothesis is that if the learning algorithm is allowed to choose the data from which it learns—to be “curious,” if you will—it will perform better with less training”。

2. 基本思想

2.1 图示

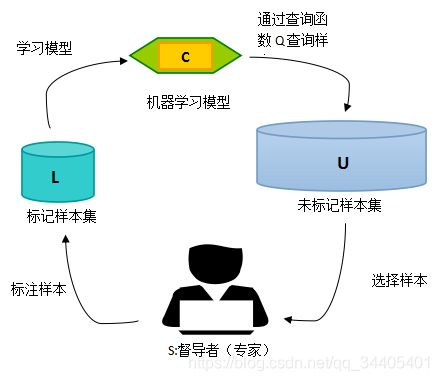
主动学习的模型如下:

A=(C,Q,S,L,U)，

其中 C 为一组或者一个分类器，L是用于训练已标注的样本。Q 是查询函数，用于从未标注样本池U中查询信息量大的信息，S是督导者，可以为U中样本标注正确的标签。学习者通过少量初始标记样本L开始学习，通过一定的查询函数Q选择出一个或一批最有用的样本，并向督导者询问标签，然后利用获得的新知识来训练分类器和进行下一轮查询。主动学习是一个循环的过程，直至达到某一停止准则为止。

2.2 策略

刚才说到查询函数Q用于查询一个或一批最有用的样本。那么，什么样的样本是有用的呢？即查询函数查询的是什么样的样本呢？在各种主动学习方法中，查询函数的设计最常用的策略是：不确定性准则（uncertainty）和差异性准则（diversity）。

对于不确定性，我们可以借助信息熵的概念来进行理解。我们知道信息熵是衡量信息量的概念，也是衡量不确定性的概念。信息熵越大，就代表不确定性越大，包含的信息量也就越丰富。事实上，有些基于不确定性的主动学习查询函数就是使用了信息熵来设计的。所以，不确定性策略就是要想方设法地找出学习器不确定性高的样本，因为这些样本所包含的丰富信息量，对我们训练模型来说就是有用的。

那么差异性怎么来理解呢？之前说到或查询函数每次迭代中查询一个或者一批样本。我们当然希望所查询的样本提供的信息是全面的，即加入到训练集中各个样本提供的信息不重复不冗余，即样本之间具有一定的差异性。因此差异性经常与多样性结合使用，即在一次主动学习中查询到了一批最不确定的样本，然后在这些样本中挑出差异性大的样本去人工标注。因此在我看来，很多论文里讲的数据多样性、数据代表性其实就是差异性！

3. 算法

3.1 基于流、基于池

根据获得未标注数据的方式，可以将主动学习分为两种类型：基于流的和基于池的。

基于流(stream-based)的主动学习中，未标记的数据按先后顺序逐个提交给选择引擎，由选择引擎根据某些评价指标决定是否标注当前提交的样例，如果不标注，则将其丢弃。

基于池(pool-based)的主动学习通常是离线、反复的过程。比如有一个未标注数据的集合，由选择引擎在该集合中选择当前要标注的数据(数据被选择经人工标注加入到训练数据集后，要在未标注数据集中删除)。在此过程的每个迭代周期，主动学习系统都会选择一个或者多个未标记数据进行标记并用于随后的模型训练，直到预算用尽或者满足某些停止条件为止(未标注数据用光了也是一种条件、或者模型准确率达到了某个值)。

现在常用的AL算法都是基于池的。

3.2 类别

主动学习方法有多种划分方式：
1.根据与机器学习模型或者深度学习模型结合的划分方式，对于ALPS这种方法还好，然而对于Entropy、Margin这种根据模型分类概率计算的方法却难以界定；2.根据主动学习方法采样数据的方式划分：基于数据流或数据池，现在所能见到的主动学习方法几乎都是基于数据池采样的，基于数据流的主动学习方法已经很少见；3.根据对模型的作用：比如基于不确定度缩减，基于版本缩减，基于泛化误差缩减，这种划分方式难以衡量目前很多同时有多个作用的主动学习方法，比如Learn-loss；4.最后一种就是基于数据选择策略（不确定性、多样性）划分的，虽然目前没有基于这种划分方式的研究综述，但是在近几年的主动学习论文中，通过数据选择策略划分主动学习方法逐渐流行，且成为规范。本文基于这种划分方式进行介绍。

个人感觉AL最终的分类就是刚开始提到的策略：基于不确定性策略、基于差异性(多样、代表)策略

3.3 算法(这里只介绍基本的)

3.3.1 基于不确定性

https://modal-python.readthedocs.io/en/latest/content/query_strategies/uncertainty_sampling.html
1）基于置信度（Least Confidence）
用1减去数据预测概率分布中的最大概率(概率分布由任务分类模型得出)，然后选取差值最大的
2）基于后验概率的信息熵(衡量样例所含信息量大小)：(分类任务)

modAL框架里对其描述：

信息熵公式和python代码:
计算信息熵的公式：n是类别数，p(xi)是第i类的概率

已标注数据集的每个类的信息熵计算：

from math import log
 
def InformationEntropy(dataSet):
    numEntries = len(dataSet) # 样本数
    labelCounts = {} # 该数据集每个类别的频数
    for featVec in dataSet:  # 对每一行样本
        currentLabel = featVec[-1] # 该样本的标签
        if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1 
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries # 计算p(xi)
        shannonEnt -= prob * log(prob, 2)  # log base 2
    return shannonEnt

未标注数据中单个数据的信息熵计算：
假设已经用分类器预测出每个类的概率为probability_list=[0.0012939334847033024, 0.010607522912323475, 6.619166379095986e-05, 0.0005499138496816158, 0.008771012537181377, 0.009928485378623009, 0.002862347522750497, 0.8593437671661377, 0.0020671547390520573, 0.10438258945941925, 0.0001270791981369257]

信息熵计算代码:

from math import log

#定义信息熵计算
def InformationEntropy(probability_list):
    shannonEnt = 0.0
    for val in probability_list:
        shannonEnt -= val * log(val, 2)  # log base 2
    return shannonEnt

总结:以上代码是已标注数据集中每一类的信息熵；未标注的单个数据信息熵则是要先用分类器对无标注数据进行每个分类的概率预测，然后再带入公式计算每一条数据的信息熵。

总结:虽然方法很简单，效果虽然说不上最好，但也是出奇的不错了！

基于信息熵抽样估计的统计学习查询策略 曲豫宾；陈翔

3）基于委员会：(分类任务)

构成一个委员会，然后选择委员会中的假设预测分歧最大的样例进行标注。
基于投票熵来选择数据(截取一篇论文，还有基于相对熵的，以及基于Jensen-Shannon分歧度都在下面这篇论文里，位置与下面图片显示的内容紧挨着)(Jensen-Shannon分歧度是基于样本对每一类别的概率，不是简单基于某一类的个数)：

基于专家委员会的主动学习算法研究 梁延峰

总结:在如今的深度学习中，委员会的成员其实就是多个模型，每个模型训练时候要与其他模型不一样，因此训练数据就得不一样，对于珍贵的标签数据来讲，这挺浪费的，所以一般不推荐

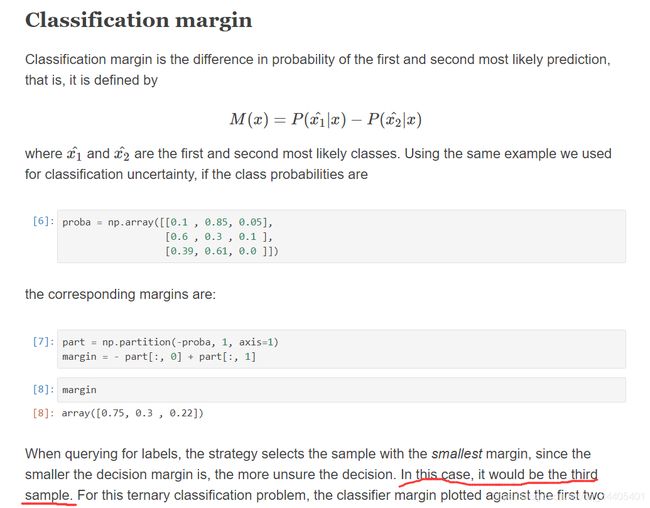
4)基于后验概率的margin(分类任务)：BvSB算法

modAL框架里对margin的描述：

BvSB：

BvSB准则中只考虑样本分类可能性最大的两个类别，忽略其他对该样本的分类结果影响较小的类别。具体选择方法为选择最优类和次优类的概率差值最小的样本。然而在BvSB准则中存在一个问题，即样本选择的过程中只考虑了样本的分类不确定性，而忽视了样本的代表性(差异性)。

基于BvSBHC的主动学习多类分类算法 曹永锋；陈荣；孙洪

3.3.2 多样性(一般与不确定性结合)

在AL算法中，几乎没有完全基于差异性的算法。一般情况下差异性只是对不确定性的一种辅助！

1)BvSBHC算法(分类任务)

从以上对BvSB准则的分析可看出，在样本选择的过程 中，仅考虑样本的分类不确定性还不够，同时也应考虑样本的 代表性。代表性可从两个方面来体现： １）从与已选出的训练样本集之间的关系来讲，新选出的 样本与已有样本之间应该具有低的信息冗余。 ２）从与整个未标注样本集之间的关系来讲，新选出的样 本应具有较高的代表性，即该样本一旦被加入到训练样本集 中，能够使训练样本集更好地代表整个未标注样本集。

基于BvSBHC的主动学习多类分类算法 曹永锋；陈荣；孙洪

4.应用

deep learning中，分类任务、回归任务以及分类与回归的任务中，只要你想用，你就可以可以使用AL！但是，AL更常用于分类任务中，也可能因为分类任务比较常见！

代码

https://github.com/duruiting/Active-Learning