论智能出现的简约性和自恰性原理（上）

背景和动机

神经科学中的研究认为大脑的世界模型是解剖上高度结构化（如模块化的大脑区域和柱状体组织），功能性的（如稀疏编码和子空间编码）。这样一个结构化模型是大脑感知、预测、做智能决策效率与有效性的关键。
相比较，在过去十年，人工智能的进步主要基于使用“蛮力”训练模型的深度学习方法，在这种情况下，虽然 AI 模型也能获得功能模块来进行感知与决策，但学习到的特征表示往往是隐式的，难以解释。
此外，单靠堆算力来训练模型，也使得 AI 模型的规模不断增大，计算成本不断增加，且在落地应用中出现了许多问题，如神经崩溃导致学习到的表征缺少多样性，模式崩溃导致训练缺乏稳定性，模型对适应性和对灾难性遗忘的敏感性不佳，却反对形变或对抗攻击的鲁棒性等等。

假设这些问题出现的基本原因是当前深度神经网络和人工智能缺乏对智能系统功能组织原理的系统和集成的理解。例如用于分类的判别模型和用于采样或重放的生成模型的训练在大部分情况下是分开的。此类模型通常是开环系统，需要通过监督或自监督进行端到端的训练。而维纳等人早就发现，这样的开环系统不能自动纠正预测中的错误，也不能适应环境的变化。

因此，他们主张在控制系统中引入“闭环反馈”，让系统能够学习自行纠正错误。在这次的研究中，他们也发现：用判别模型和生成模型组成一个完整的闭环系统，系统就可以自主学习（无需外部监督），并且更高效，稳定，适应性也强。
我们引入简约性和自一致性两个原理来回答下列问题：

• 学什么：从数据学习的目标是什么以及如何测量
• 怎么学：怎样通过效率的有效的计算达到这个目标

第一个问题的答案很自然落到信息编码理论上，也就是学习精确地量化测量数据信息找到最紧致的表示，当学习的目标清晰并明确后，第二个问题的答案很自然落到控制/博弈论领域,这提供了一个统一的有效计算框架，即闭环反馈系统，以此得到任意测度下的目标一致性，如图1所示：

图1：通过一个压缩闭环转录为感观数据找到一个紧致的结构化的模型

两个原理背后的基本想法是可以追根溯源的，人工神经网络最早作为感知器(Rosenblatt, 1958)的灵感是可以有效存储和组织感知信息，后向传播 (Kelley, 1960; Rumelhart et al., 1986)时候来提出用于学习这些模型的机制。甚至在神经网络感知前，Norbert Wiener已经开始思考系统级学习的计算机制了。在他著名的书 Cybernetics (Wiener, 1948)中，他研究了信息压缩之于简约性、学习机中的反馈/博弈之于一致性可能的角色。

智能的两个原理：简约性与自洽性

本文提出了解释人工智能构成的两个基本原理，分别是简约性与自洽性（也称为“自一致性”），并以视觉图像数据建模为例，从简约性和自洽性的第一原理推导出了压缩闭环转录框架。

学什么：简约性原理

”Entities should not be multiplied unnecessarily.”
– William of Ockham
所谓简约性，就是“学习什么”。简约性是必须的，如果观察外部世界没有什么低维结构，那就没什么值得学习或记忆的。这个原理不是简单地为了节省智能系统的能量、时间、空间等资源。简约性不是让系统达到最大的压缩率，而是通过计算有效的方法获得紧致的结构化的表达。如果一个智能系统试着用Kolmogorov复杂度或香农信息论压缩数据，那它们不仅难以计算而且会得到非结构化的表示。真要以香农信息论得到数据的最小描述长度要求最小化Helmholtz自由能，就是典型的难以计算。仔细审查许多常见的模型好坏的数学或统计测度，要么对于一个通用的高维模型计算代价是指数级昂贵，要么甚至对于数据分布的低维表示是不明确的，如最大似然度、KL散度、互信息、JS散度、Wasserstein距离。

那一个智能系统该如何以计算有效的方式在观察中嵌入简约性来识别和表示结构？理论上，智能系统可以使用任何描述世界的结构化模型，只要它们能够简单有效地模拟现实感官数据中的有用结构。系统应该能够准确有效地评估学习模型的好坏，并且使用的衡量标准是基础、通用、易于计算和优化的。

具体地，该如何建模和计算简约性，令感知高维数据样本$x$，低维表示为$z$，学习的目的就是要建立一个映射f，使$x$到$z$，$z$是紧致结构化的：
$$x\in {\Re }^D\stackrel{f(x,\theta )}{}z\in {\Re }^d$$
紧致意味着存储是经济的，结构化意味着访问和使用是高效的，特别的，线性结构对插值和推断是理想的。

以视觉数据建模为例，简约原理试图找到一个（非线性）变换 f 来实现以下目标：

• 压缩：将高维感官数据 x 映射到低维表示 z；
• 线性化：将分布在非线性子流形上的每一类对象映射到线性子空间；
• 划痕（scarification）：将不同的类映射到具有独立或最大不连贯基的子空间。

也就是将可能位于高维空间中的一系列低维子流形上的真实世界数据分别转换为独立的低维线性子空间系列。这种模型称为“线性判别表示”（linear discriminative representation，LDR），压缩过程如图 2 所示：

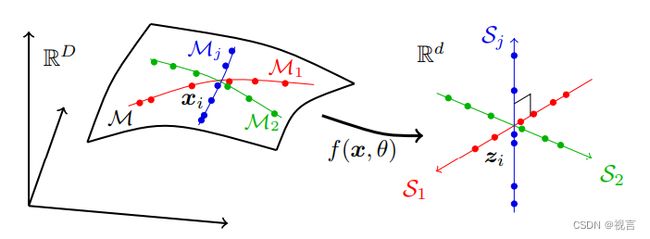
图 2：寻求线性和判别表示，将通常分布在许多非线性低维子流形上的高维感官数据映射到与子流形具有相同维度的独立线性子空间集。

在 LDR 模型系列中，存在衡量简约性的内在度量。也就是说，给定一个 LDR，我们可以计算所有子空间上的所有特征所跨越的总“体积”以及每个类别的特征所跨越的“体积”之和。然后，这两个体积之间的比率给出了一个自然的衡量标准，表明 LDR 模型有多好（往往越大越好）。

图3： 所有特征的比例$R=log\#(蓝色球+绿色球)$，两个子空间的特征比例$R^c=log\#(绿色球),比例减少就是两个比例的差：\Delta R=R-R^c$$
图3展示了特征分布在两个子空间的样例。左右模型的本证复杂度是一样的。很明显，左边的配置作为特征更好，它不同类是独立正交的。

根据信息论，分布的体积可以通过其率失真来衡量。简略地讲，率失真是有多少$ϵ$-球 或球体可以塞进分布张成的空间的对数。球个数的对数就解释成以$ϵ$的精度编码一个分布的随机采样需要多少二进制比特。这就是熟知的描述长度。

令$R$为所有k类采样数据 $X\doteq [x^1,\dots ,x^n]$ 的所有特征 $\mathbb{Z}\doteq [z^1,\dots ,z^n]$的联合分布的率失真，$R^c$ 是所有 $k$ 类率失真的平均: $R^c(\mathbb{Z})=\frac{1}{k}[R({\mathbb{Z}}_1)+\cdots +R({\mathbb{Z}}_k)]$ ，其中 $\mathbb{Z}={\mathbb{Z}}_1\cup \cdots \cup {\mathbb{Z}}_k$. 因为对数，整体和部分和的比率变成差:
$$\Delta R(\mathbb{Z})\doteq R(\mathbb{Z})-R^c(\mathbb{Z}),$$
这就给出了一个最基本的，锱铢必较的$\mathbb{Z}$的度量。

虽然在高维的空间分布中，率失真和许多其他度量一样，是难以计算的，NP难的，但是如果$\mathbb{Z}$ 是从子空间上的高斯分布采样，则其具有闭合形式：
$$R(\mathbb{Z})\doteq \frac{1}{2}\log \det \left(I+\alpha \mathbb{Z}{\mathbb{Z}}^{\ast }\right).$$

于是可以被有效计算和优化!

如果用高斯函数的率失真且选择一个深网络(如 resnet)来建模映射$f(x,\theta )$，则最大化编码率失真就是熟知的MCR${}^2$ 原理

$$\underset{\theta }{\max }\Delta R(\mathbf{Z}(\theta ))=R(\mathbb{Z}(\theta ))-R^c(\mathbb{Z}(\theta )),$$
可以有效地将一个多类别的视觉数据映射到一个多维正交的子空间。注意到，最大化第一项$R$拓展了所有特征的体积。它同时构建了所有特征的对比学习，比一些经典方法构建对比样本对要高效地多。最小化第二项$R^c$压缩和线性化了每个类别的特征，这可以解释成为每个类构建对比学习

通过最大化比率衰减，不同类的特征会变得独立，每个类别的特征几乎均匀分布在每个子空间。而广为使用的交叉熵把一个类别映射到one-hot标签，它把每个类别的特征最终映射到一个一维实例上。

深度神经网络是只是建立一个x到z的映射f，那智能系统如何知道f首先应该使用哪个模型簇？回想我们的目标是优化特征集合$\mathbb{Z}$的函数$\Delta R(\mathbb{Z})$。我们从原始数据 ${\mathbb{Z}}_0=X$出发增量优化$\Delta R(\mathbb{Z})$，也就是投影梯度下降(PGA) 方案

$${\mathbf{Z}}_{\ell +1}\propto {\mathbf{Z}}_{\ell }+\eta \cdot \frac{\partial \Delta R}{\partial \mathbf{Z}}{|}_{{\mathbf{Z}}_{\ell }}subjectto\Vert {\mathbf{Z}}_{\ell +1}\Vert =1.$$
这个比例衰减的过程如图4所示：

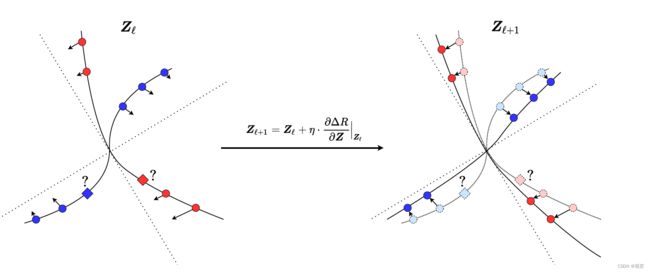
*图4：一个构建非线性映射$f$的基本方法: 按照比例衰减 $\Delta R$ 的梯度流 $\frac{\partial \Delta R(\mathbb{Z})}{\partial \mathbb{Z}}$ , 我们逐渐在非线性子流形上线性化和压缩特征，并分离不同的子流形到各自正交的子空间(两条虚线) *

带入上面高斯分布下率失真的闭合形式，我们可以计算$\Delta R=R-R^c$ 闭合形式下的梯度。如第一项$R$的梯度：

$$\begin{gathered} \frac{\partial R(\mathbb{Z})}{\partial \mathbb{Z}}{|}_{{\mathbb{Z}}_{\ell }}=\frac{1}{2}\frac{\partial \log \det (I+\alpha \mathbb{Z}{\mathbb{Z}}^{\ast })}{\partial \mathbb{Z}}{|}_{{\mathbb{Z}}_{\ell }} \\ =\alpha (I+\alpha {\mathbb{Z}}_{\ell }{\mathbb{Z}}_{\ell }^{\ast }{)}^{-1}{\mathbb{Z}}_{\ell }\doteq E_{\ell }{\mathbb{Z}}_{\ell }. \end{gathered}$$
类似地，我们可以计算$R^c$中$k$ 项 $\{R({\mathbb{Z}}_i){\}}_{i=1}^k$ 的梯度，获得${\mathbb{Z}}_{\ell }$上的 $k$ 个算子，记为$C_i$。则第二项梯度：

$$\begin{gathered} z_{\ell +1}\propto z_{\ell }+\eta \cdot [{\mathbf{E}}_{\ell }{z}_{\ell }+\mathbf{\sigma }([{\mathbf{C}}_{\ell }^1{z}_{\ell },\dots ,{\mathbf{C}}_{\ell }^k{z}_{\ell }]\left)\right] \\ subjectto\Vert z_{\ell +1}\Vert =1, \end{gathered}$$

其中 ${\mathbf{E}}_{\ell }$ 和 ${\mathbf{C}}_{\ell }$’s 是完全取决于前一层${\mathbb{Z}}_{\ell }$特征协方差的线性算子。$\sigma$ 是一个softmax算子，它把$z_{\ell }$分配给和它距离最近的类别，距离通过${\mathbf{C}}_{\ell }{z}_{\ell }$度量。每个迭代的所有算子如图5左边所示。

2022年的一个工作“ReduNet: A White-box Deep Network from the Principle of Maximizing Rate Reduction”表明，如果使用高斯的率失真函数并选择一个通用的深度网络（比如 ResNet）来对映射 f(x, θ) 进行建模，通过最大限度地降低编码率。

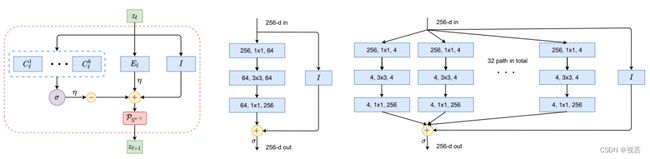
图 5：非线性映射 f 的构建块。图左：ReduNet 的一层，作为投影梯度上升的一次迭代，它精确地由扩展或压缩线性算子、非线性 softmax、跳过连接和归一化组成。图中和图右：分别是一层 ResNet 和 ResNeXt。

敏锐的读者可能已经认识到，这样的图表与 ResNet（图 5 中间）等流行的“久经考验”的深层网络非常相似，包括 ResNeXt 中的平行列（图 5 右）和专家混合（MoE）。
从展开优化方案的角度来看，这为一类深度神经网络提供了有力的解释。甚至在现代深度网络兴起之前，用于寻求稀疏性的迭代优化方案，例如 ISTA 或 FISTA 就已被解释为可学习的深度网络。
通过实验，他们证明，压缩可以诞生一种有建设性的方式来推导深度神经网络，包括它的架构和参数，作为一个完全可解释的白盒：它的层对促进简约的原理性目标进行迭代和增量优化。因此，对于如此获得的深度网络，ReduNets，从数据 X 作为输入开始，每一层的算子和参数(${\mathbf{E}}_{\ell },{\mathbf{C}}_{\ell }$)都以完全向前展开的方式构造和初始化。
这与深度学习中的流行做法非常不同：从一个随机构建和初始化的网络开始，然后通过反向传播进行全局调整。人们普遍认为，由于需要对称突触和复杂的反馈形式，大脑不太可能利用反向传播作为其学习机制。在这里，前向展开优化只依赖于可以硬连线的相邻层之间的操作，因此更容易实现和利用。
此外，如此构建的参数和算子都有责任进行另一个优化层次的finetune，比如反向传播实现的梯度下降方法。但这里不要混淆用于finetune网络的梯度下降和网络层是为了实现梯度优化。

假如我们进一步希望学习到的编码对于时间平移或空间转换不变的话，那我们就视每一个样本$x(t)$ 和它所有的平移版本$\{x(t-\tau )\forall \tau \}$为等价类。如果我们把它们压缩和线性化到同一个子空间，则在上述梯度操作中的线性算子$\mathbf{E}$ or $\mathbf{C}$’s，都自动变成多通道卷积。

一旦我们意识到深度网络本身的作用是进行（基于梯度的）迭代优化以压缩、线性化和稀疏化数据，那么就很容易理解过去十年人工神经网络的“进化”，尤其有助于解释为什么只有少数 AI 系统通过人工选择过程脱颖而出：从 MLP 到 CNN 到 ResNet 到 Transformer。
相比之下，网络结构的随机搜索，例如神经架构搜索，并没有产生能够有效执行一般任务的网络架构。他们猜想，成功的架构在模拟数据压缩的迭代优化方案方面变得越来越有效和灵活。前面提到的 ReduNet 和 ResNet/ResNeXt 之间的相似性可以例证。当然，还有许多其他例子。

而transformer在transform什么呢？注意到一个率失真项$R(\mathbb{Z})$的梯度是$\frac{\partial R}{\partial \mathbb{Z}}=\alpha (I+\alpha {\mathbb{Z}}_{\ell }{\mathbb{Z}}_{\ell }^{\ast }{)}^{-1}{\mathbb{Z}}_{\ell }$。不把矩阵$\alpha (I+\alpha {\mathbb{Z}}_{\ell }{\mathbb{Z}}_{\ell }^{\ast }{)}^{-1}$视作$E_{\ell }$作用在${\mathbb{Z}}_{\ell }$上的一个线性算子，我们可以重新梯度的近似：

$$\begin{gathered} \alpha (I+\alpha {\mathbb{Z}}_{\ell }{\mathbb{Z}}_{\ell }^{\ast }{)}^{-1}{\mathbb{Z}}_{\ell }\approx \alpha (I-\alpha {\mathbb{Z}}_{\ell }{\mathbb{Z}}_{\ell }^{\ast }){\mathbb{Z}}_{\ell } \\ =\alpha [{\mathbb{Z}}_{\ell }-\alpha {\mathbb{Z}}_{\ell }({\mathbb{Z}}_{\ell }^{\ast }{\mathbb{Z}}_{\ell })]. \end{gathered}$$
这里优化率失真项的梯度操作主要依赖于早先迭代特征$\mathbf{A}\doteq {\mathbb{Z}}_{\ell }^{\ast }{\mathbb{Z}}_{\ell }$的自动矫正。这就是熟知的self-attention或self-expression。如果我们考虑为上式每个特征项应用一个额外的线性转换$U$ ，则梯度迭代项为：
$${\mathbb{Z}}_{\ell +1}\doteq {\mathbb{Z}}_{\ell }+U_o[{\mathbb{Z}}_{\ell }-\alpha U_v{\mathbb{Z}}_{\ell }(U_k{\mathbb{Z}}_{\ell }{)}^{\ast }(U_q{\mathbb{Z}}_{\ell })].$$
这就是Transformer每层基本操作的精确形式，即一个self-attention (SA) 头接一个前向反馈残差MLP操作。

此外，非常类似于ResNeXT vs ResNet，对于图像分类这样的网络，每层同时使用$k$个SA头经验上会更好。在比率约减的背景下，这些SA头很自然的可以被解释成与比率约减$\Delta R(\mathbb{Z})=R(\mathbb{Z})-[R({\mathbb{Z}}_1)+\cdots +R({\mathbb{Z}}_k)]/k$中的多个率失真项相关的梯度项。SA头中学习到的线性变换项 $(U_k,U_q,U_v)$ 可以被解释成在流形上选择和转换属于同一类(信号或图像的) token sets的匹配滤波器或者稀疏字典。因此我们猜测Transformer层模仿了一个基于梯度迭代方案的更通用的簇，通过聚类、压缩、线性化它们来优化所有输入token sets (在多个流形上)的比率约减。

此外，基于展开迭代方案的网络可能是最有效的，可以猜测除了梯度下降外，更高级的优化方案，如加速梯度下降，可能在未来会获得更有效的深度神经网络结构。从架构上说，这些加速方法需要引入多层间的跳连。这可能从优化的视角帮助解释了为什么额外的跳连在highway网络或密集网络汇总尝尝能提高网络有效性。

如何学：自洽性原理

“Everything should be made as simple as possible, but not any simpler.”
– Albert Einstein

自洽性是关于“如何学习”，即自主智能系统通过最小化被观察者和再生者之间的内部差异来寻求最自洽的模型来观察外部世界。
仅凭借简约原理并不能确保学习模型能够捕获感知外部世界数据中的所有重要信息。例如，通过最小化交叉熵将每个类映射到一维“one-hot”向量，可以被视为一种简约的形式。它可能会学习到一个好的分类器，但学习到的特征会崩溃为单例，称为“神经崩溃”。如此学习来的特征不包含足够的信息来重新生成原始数据。即使我们考虑更一般的 LDR 模型类别，单独的比率约减目标也不会自动确定环境特征空间的正确维度。如果特征空间维度太低，学习到的模型会欠拟合数据；如果太高，模型可能会过拟合。
感知的目标是学习一切可预测的感知内容。智能系统应该能够从压缩表示中重新生成观察到的数据的分布，生成后，无论它尽再大的努力，它自身也无法区分这个分布。

所以自洽的原理就是：为外部世界的观察寻找一个最自洽的模型，使得观察与重新生成的内部差异最小化。

论文强调，自洽和简约这两个原理是高度互补的，应该始终一起使用。仅靠自洽不能确保压缩或效率方面的增益。在数学和计算上，使用过度参数化的模型拟合任何训练数据或通过在具有相同维度的域之间建立一对一映射来确保一致性，而不需要学习数据分布中的内在结构是很容易的。只有通过压缩，智能系统才能被迫在高维感知数据中发现内在的低维结构，并以最紧凑的方式在特征空间中转换和表示这些结构，以便将来使用。
此外，只有通过压缩，我们才能容易地理解过度参数化的原因，比如，像 DNN 通常通过数百个通道进行特征提升，如果其纯粹目的是在高维特征空间中进行压缩，则不会导致过度拟合：提升有助于减少数据中的非线性，从而使其更容易压缩和线性化。后续层的作用是执行压缩（和线性化），通常层数越多，压缩效果越好。

为了确保学习到的特征映射$f$和表达$z$正确捕捉到了数据中的低维结构，可以检查是否压缩特征$z$能够通过$\eta$参数化的生成映射$g$重新产生原始数据$x$
$$x\in {\Re }^D\stackrel{f(x,\theta )}{}z\in {\Re }^d\stackrel{g(z,\eta )}{}\hat{x}\in {\Re }^D,$$
从某种意义上，$\hat{x}=g(z,\eta )$ 接近 $x$(根据合适的度量)。这个过程就是熟知的$auto-encoding$。
在压缩到诸如 LDR 之类的结构化表示的特殊情况下，论文将一类自动编码（具体见原论文）称为“转录”（transcription）。这里的难点在于如何使目标在计算上易于处理，从而在物理上可以实现。更准确地说，什么是$x$与$\hat{x}$之间差异的数据上定义良好以及计算有效的度量？前面说到很多度量都是不明确的或计算上难以处理的，甚至高斯分布和它的混合模型。如何解决这个与高维空间退化分布相比相关，基本的但在计算性上未被公开承认的困难？

前面说到的 $\Delta R$给出了退化分布之间的定义良好的首要距离度量。但它仅适用于子空间或高斯的混合，而不适用于一般分布！而我们只能期望内部结构化表示 z 的分布是子空间或高斯的混合，而不是原始数据 x。
这导致了一个关于学习“自洽”表示的相当深刻的问题：为了验证外部世界的内部模型是否正确，自主系统真的需要测量数据空间中的差异吗？
答案是否定的。

关键是要意识到，要比较$x$ 和 $\hat{x}$， 智能体只需要通过相同的映射$f$比较它们各自的内部特征 $z=f(x,\theta )$ 和 $\hat{z}=f(\hat{x},\theta )$，来使 z 紧凑和结构化。
$$x\stackrel{f(x,\theta )}{}z\stackrel{g(z,\eta )}{}\hat{x}\stackrel{f(x,\theta )}{}\hat{z}.$$

测量 $z$ 空间中的分布差异实际上是定义明确且有效的：可以说，在自然智能中，学习内部测量差异是有独立自主系统的大脑唯一可以做的事情。
这有效地生成了一个“闭环”反馈系统，整个过程如图 6 所示。编码器$f$现在作为判别器的额外角色，通过内部特征$z$与$\hat{z}$的差异，检测$x$与$\hat{x}$之间任何差异。$z$与$\hat{z}$分布的距离能够通过它们样本$\mathbb{Z}(\theta )$ 与$\hat{\mathbb{Z}}(\theta ,\eta )$的比率约减来度量：
$$\Delta R(\mathbb{Z}(\theta ),\hat{\mathbb{Z}}(\theta ,\eta ))\doteq R(\mathbb{Z}\cup \hat{\mathbb{Z}})-\frac{1}{2}(R(\mathbb{Z})+R(\hat{\mathbb{Z}})).$$

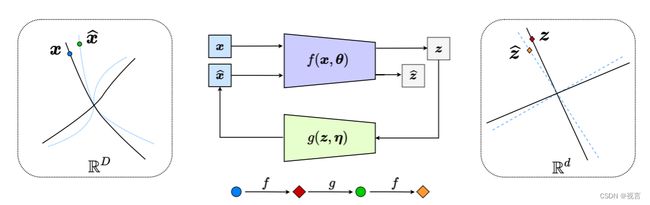
图 6：非线性数据子流形到 LDR 的压缩闭环转录（通过在内部比较和最小化 z 和 $\hat{z}$ 的差异）。这导致了编码器/传感器 f 和解码器/控制器 g 之间的自然追逃博弈，使解码的 $\hat{x}=$（蓝色虚线）的分布追逐并匹配观察到的数据 x（黑色实线）的分布。

人们可以将单独学习 DNN 分类器 f 或生成器 g 的流行做法解释为学习闭环系统的开放式部分（图 6）。这种目前流行的做法与开环控制非常相似，控制领域早已知道它存在问题且成本高昂：训练这样的部分需要对期望的输出（如类标签）进行监督；如果数据分布、系统参数或任务发生变化，这种开环系统的部署本质上是缺少稳定性、鲁棒性或自适应性的。例如，在有监督的环境中训练的深度分类网络，如果重新训练来处理具有新数据类别的新任务，通常会出现灾难性的遗忘。

相比之下，闭环系统本质上更加稳定和自适应。事实上，Hinton 等人在1995年就已经提出了这一点。判别和生成部分需要分别作为完整学习过程的“唤醒”和“睡眠”阶段结合起来。
然而，仅仅闭环是不够的。我们只考虑优化生成器$g$来最小化$z$和$\hat{z}$的差异，按照比率测度表达就是：
$$\underset{\eta }{\min }\Delta R(\mathbb{Z}(\theta ),\hat{\mathbb{Z}}(\theta ,\eta )).$$

注意到 $\Delta R(\mathbb{Z},\hat{\mathbb{Z}})=0$ ，如果$\hat{\mathbb{Z}}=g(f(\mathbb{Z}))=\mathbb{Z}$. 特征$\mathbb{Z}$ 的最优集合应该是编码解码循环的不动点。但是编码器$f$做了很大的维数约简和压缩，因此$\hat{\mathbb{Z}}=\mathbb{Z}$不能完全代表$\hat{X}=X$。简单起见，考虑当$X$已经在线性子空间了(比如$k$维)，$f$ 和 $g$是线性投影和提升。$f$不能检测到零空间的任何差异：$X$ 与任何 $\hat{X}=X+null(f)$在$f$下都有同样的像。
那$\hat{\mathbb{Z}}=\mathbb{Z}$ 能意味着 $\hat{X}=X$ 吗？换句话说，在内部空间满足自洽性准则怎么保证准确地重构观察数据？可能只有当维数$k$足够小，$f$可以进一步调整时才行。让我们假设$X$ 的维数是 $k<d/2$，$d$是特征空间的维数。则在一个线性提升$g$下，$\hat{X}=g(f(X))$维数是$k$-维的子空间。 $X$ and $\hat{X}$两个子空间的并的维度最多$2k<d$。因此，如果这连个子空间之间有一个差异且$f$可以是任意投影，我们有 $f(X)\ne f(\hat{X})$，即$X\ne \hat{X}$ 意味着 $\mathbb{Z}\ne \hat{\mathbb{Z}}$。

因此，$g$最小化了错误$\Delta R$后，如果$X$ and $\hat{X}$有差异，$f$需要主动调整和检测。这个过程能在编码器$f$和解码器$g$之间重复，导致一个很自然的追逃博弈，如图6所示。

论文主张任何智能体都需要一种内部博弈机制，以便能够通过自我批评进行自我学习！这当中遵循的是博弈作为一种普遍有效的学习方式的概念：反复应用当前模型或策略来对抗对抗性批评，从而根据通过闭环收到的反馈不断改进模型或策略！
在这样的框架内，编码器 f 承担双重角色：除了通过最大化比率约减 $\Delta R(\mathbb{Z})$来学习数据 $x$的表示 $z$（如简约性那节中所做的那样），它还应该作为反馈“传感器”，主动检测数据 $x$ 和生成的 $\hat{x}$ 之间的差异。解码器 $g$ 也承担双重角色：它是控制器，纠正 $f$ 所检测到的 $x$ 和 $\hat{x}$ 之间的差异；同时又是解码器，尝试将整体的编码率最小化来实现目标（关于给定的准确度）。
因此，最优的“简约”和“自洽”表示元组 (z, f, g) 可以解释为 f(θ) 和 g(η) 之间的零和博弈的平衡点，而不是组合基于比率约减的效用：

$$\underset{\theta }{\max }\underset{\eta }{\min }\Delta R\left(\mathbb{Z}\right)+\Delta R\left(\hat{\mathbb{Z}}\right)+\Delta R(\mathbb{Z},\hat{\mathbb{Z}}).$$
最近的一个分析严格地展示了，当输入数据$X$分布在多线性空间时，期望的最优表示$\mathbb{Z}$实际上是以一个比率约减目标依次maxmin博弈达到Stackelberg均衡的。而在多个非线性空间还是一个开放问题。尽管如此，已经有引人注目的证据表示，解决这样的博弈实际上提供了真实世界视觉数据优秀的自动编码，也为每一类别自动确定了合适维度的子空间。不会遇到训练经典生成模型，如GAN时的模式坍塌问题。学习到的表示同时具备可分性和生成性。

以上讨论是两个原理在有监督情况下的表现。
但论文强调，他们所提出的压缩闭环转录框架能够通过自我监督和自我批评来进行自我学习！
此外，由于比率约减已经为学习结构找到显式（子空间类型）表示，使得过去的知识在学习新任务/数据时更容易保留，可以作为保持自一致性的先验（记忆） 。

为了更加清晰，我们检查上面的闭环转录框架怎么拓展到增量学习—也就是说，一次学习一个物体，而不是一次同时学习多个类别。当为一个新类学习表示${\mathbb{Z}}_{new}$时，只需要增加之前的maxmin优化的开销，确保之前学习的表示${\mathbb{Z}}_{old}$ 在经过闭环转录时保持自一致(不动点)：${\mathbb{Z}}_{old}\approx {\hat{\mathbb{Z}}}_{old}=f(g({\mathbb{Z}}_{old}))$.
换句话说，上面的maxmin博弈称为一个带限制的博弈
$$\begin{gathered} \underset{\theta }{\max }\underset{\eta }{\min }\Delta R(\mathbb{Z})+\Delta R\left(\hat{\mathbb{Z}}\right)+\Delta R({\mathbb{Z}}_{new},{\hat{\mathbb{Z}}}_{new}) \\ subjectto\Delta R({\mathbb{Z}}_{old},{\hat{\mathbb{Z}}}_{old})=0. \end{gathered}$$
这样一个限制性博弈使得学习成为一个增量的动态的过程，使得学习到的转录连续适应新的数据。这个过程如图7所示：
图7：通过压缩闭环转录的增量学习. 对于一个新的数据类$X_{new}$，一个新的LDR内存${\mathbb{Z}}_{new}$是通过编码器和解码器之间一个带限制的minmax博弈学习到的，过去类别的内存${\mathbb{Z}}_{old}$是保留的，作为闭环的不动点。

最近的实证研究表明，这可以产生第一个具有固定内存的自包含神经系统，可以在不遭受灾难性遗忘的情况下逐步学习良好的 LDR 表示。对于这样一个闭环系统，遗忘（如果有的话）是相当优雅的。
此外，当再次将旧类别的图像提供给系统进行审查时，可以进一步巩固学习到的表示——这一特征与人类记忆的特征非常相似。从某种意义上说，这种受约束的闭环公式基本上确保了视觉记忆的形成可以是贝叶斯和自适应的——假设这些特征对大脑来说是理想的话。

注意这个框架是完全无监督的设置下构造的。因此尽管出于教学的目的，我们假设类信息可用才提出这些原理，但是这个框架是可以很自然地拓展到没有类信息可用的无监督配置下的。这种情况下，我们只需要把一个新的样本和它的增广视作一个新类就行了。这可以被视作一种自监督的类型。有了自批评博弈机制，一个压缩闭环转录很容易学习。
如图 8 所示，如此学习的自动编码不仅表现出良好的样本一致性，而且学习到的特征还表现出清晰且有意义的局部低维（薄）结构。

图 8：图左：在 CIFAR-10 数据集（有 10 个类别的 50,000 张图像）的无监督设置中学习的自动编码的 x 与相应解码的 x^ 之间的比较。图右：10 个类别的无监督学习特征的 t-SNE，以及几个邻域及其相关图像的可视化。注意可视化特征中的局部薄（接近一维）结构，从数百维的特征空间投影。

更令人惊讶的是，即使在训练期间没有提供任何类信息，子空间或特征相关的块对角结构也开始出现在为类学习的特征中（图 9）！因此，所学特征的结构类似于在灵长类动物大脑中观察到的类别选择区域。

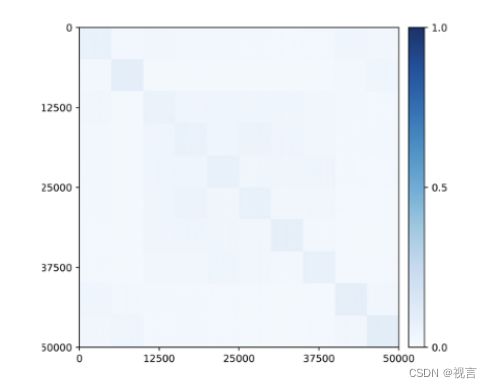
图 9：通过闭环转录，属于 10 个类别 (CIFAR-10) 的 50,000 张图像的无监督学习特征之间的相关性。与类一致的块对角结构在没有任何监督的情况下出现。

下一篇：论智能出现的简约性和自恰性原理（下）