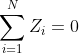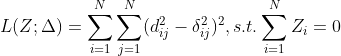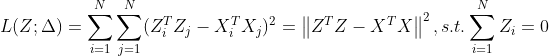表示学习(Representation Learning)(三)——流形学习

关于什么是流形和流形学习(Manifold Learning)，作为一种针对非线性数据的降维方法的算法的研究，有很多优秀的文章博客可以供大家学习，这里贴几篇文章供大家参考看看Manifold Learning | SpringerLink

https://arxiv.org/abs/2011.01307

[Goodfellow et al., 2016] Goodfellow I., Bengio Y., and Courville A. (2016): Deep Learning, MIT Press. (Section 5.11.3)

这里直接介绍三个算法思想：

1)多维缩放模型(Multi-dimensional Scaling (MDS))

2)等距离特征映射模型(Isometric Feature Mapping (ISOMAP))

3)局部线性嵌入模型(Locally Linear Embedding (LLE))

首先我们明确这些算法的目的：

这些算法都是为了实现将处于高纬度的数据集，通过一个函数变换，将原空间的数据映射到低维度空间上，且该映射要做到尽可能保留数据在原空间上点与点的距离关系。

多维缩放模型(Multi-dimensional Scaling (MDS))

给定一个高纬度数据集 ( N个样本，d个特征)的内积距离矩阵 ，其中(可以看出该算法模型的好处，不需要知道原数据的特征信息，只需要获得距离矩阵即可)，接着我们假设一个要求的目标空间p维度(p)之间的距离我们用欧拉距离进行衡量：

问题则转换成了：找到这样一组点使得其中函数映射f是一个单调的含参函数。同时为了保证结果的唯一性，应使得

(如果没有该限制，如果有这样两个解，,

就有,

则同样是一组解)

如此问题就转换成了损失函数L的最小化

一个求解方法是利用欧拉向量空间的性质：对于一个数据中心化的矩阵X，它的内积矩阵可由它的距离矩阵表示：

其中是单位矩阵

同样的在目标空间，

则损失函数

结合上一篇主成分分析中的求解方法，我们可以知道可以对这个实对称矩阵G进行谱分解

其中是对应的特征向量

则原数据在目标空间的表示

是前p个特征值组成的对角矩阵，是对应特征向量组成的矩阵

from sklearn.metrics.pairwise import euclidean_distances
def cmds(X, n_dim, input_type='raw'):
    """
    Parameters
    ----------
    X: 可以是(d, n) 也可以是(n,n) 
        
        
    n_dim: 目标空间维度
    """

    if input_type == 'distance':
        D = X
    elif input_type == 'raw':
        Xt = X.T
        D = euclidean_distances(Xt,Xt)
        

    N = D.shape[0]
    D2 = D**2
    H = np.eye(N) - 1/N
    T = -0.5*np.dot(np.dot(H,D2),H)
    evals,evecs = np.linalg.eig(T) 
    Y = np.dot(evecs[:,:n_dim],np.diag(np.sqrt(evals[:n_dim])))
    return Y.T, evals[0:n_dim], evecs[0:n_dim]

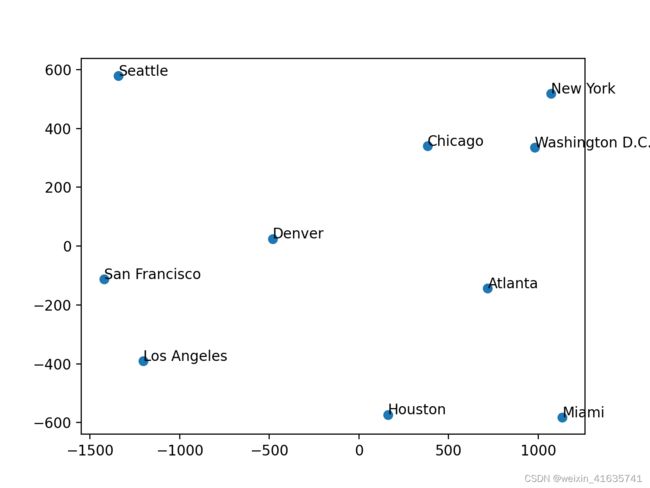
def ten_city():
    city_name = ['Atlanta', 'Chicago', 'Denver', 'Houston', 'Los Angeles', 'Miami', 'New York', 'San Francisco', 'Seattle', 'Washington D.C.']
    num_city = len(city_name)
    data = np.zeros([num_city, num_city])
    data[1,0] = 587
    data[2,0] = 1212; data[2,1] = 920
    data[3,0] = 701;  data[3,1] = 940;  data[3,2] = 879
    data[4,0] = 1936; data[4,1] = 1745; data[4,2] = 831;  data[4,3] = 1374
    data[5,0] = 604;  data[5,1] = 1188; data[5,2] = 1726; data[5,3] = 968;  data[5,4] = 2339
    data[6,0] = 748;  data[6,1] = 713;  data[6,2] = 1631; data[6,3] = 1420; data[6,4] = 2451; data[6,5] = 1092
    data[7,0] = 2139; data[7,1] = 1858; data[7,2] = 949;  data[7,3] = 1645; data[7,4] = 347;  data[7,5] = 2594; data[7,6] = 2571
    data[8,0] = 2182; data[8,1] = 1737; data[8,2] = 1021; data[8,3] = 1891; data[8,4] = 959;  data[8,5] = 2734; data[8,6] = 2408; data[8,7] = 678
    data[9,0] = 543;  data[9,1] = 597;  data[9,2] = 1494; data[9,3] = 1220; data[9,4] = 2300; data[9,5] = 923;  data[9,6] = 205;  data[9,7] = 2442; data[9,8] = 2329
    return data, city_name



flying_dist, city = ten_city()
flying_dist = flying_dist + flying_dist.T

 

n_dim = 2
Y_city, evals_city, evecs_city = cmds(flying_dist, n_dim, input_type='distance')

x=[]
y=[]
Y_city = Y_city.T
for i in range(len(Y_city)):
    x.append(Y_city[i][0])
    y.append(Y_city[i][1])
plt.figure("2-D")
plt.scatter(x, y)
for i in range(len(x)):
    plt.annotate(city[i], xy = (x[i], y[i]), xytext = (x[i]+0.1, y[i]+0.1)) # 这里xy是需要标记的坐标，xytext是对应的标签坐标
plt.show()