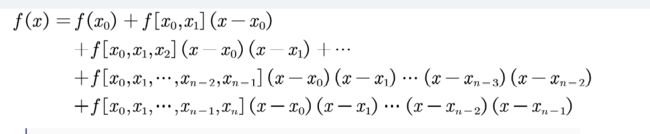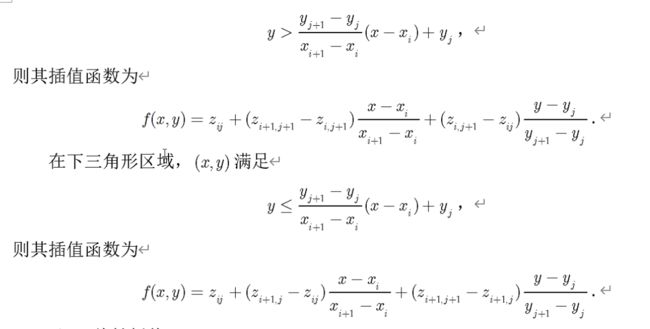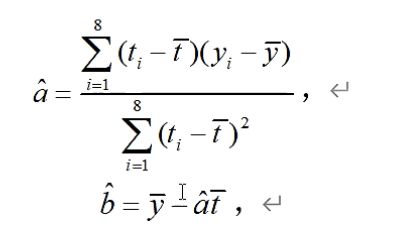插值拟合算法
一.插值算法
1.插值概念
构造一个函数使得所有已知点在函数图像上
2.一维插值插值方法
(1)一般多项式插值
(4)牛顿插值
(6)三次样条插值
数学建模中拉格朗日插值和牛顿插值算法其实并不常见,这里不过多介绍。
插值存在的问题:插值多项式的项数越高,可能会出龙格现象。尽量不要使用高次差值。
解决方法:分段低次插值
常见插值:埃尔米特插,三次样条插值
二.Matlab实现
(1)拉格朗日插值
function y=lagrange(x0,y0,x)
%拉格朗日插值函数
%n 个节点数据以数组 x0, y0 输入(注意 Matlat 的数组下标从1开始),
%m 个插值点以数组 x 输入,输出数组 y 为 m 个插值
n=length(x0);
m=length(x);
for i=1:m
z=x(i);
s=0.0;
for k=1:n
p=1.0;
for j=1:n
if j~=k
p=p*(z-x0(j))/(x0(k)-x0(j));
end
end
s=p*y0(k)+s;
end
y(i)=s;
end
先将上面的复制到Matlab函数命令下,然后运行下方实例
x0=1:1:20;
y0=x0.^2-20*x0-5;
x=1:0.1:20;
z=lagrange(x0,y0,x);
plot(x,z,':',x0,y0,'ko');
(2)分段三次埃尔米特插值
直接使用得到的多项式次数较高,存在龙格现象,因此实际应用中,往往使用分段三次埃尔米特插值。
% 分段三次埃尔米特插值
x = -pi:pi; y = sin(x);
new_x = -pi:0.1:pi;
p = pchip(x,y,new_x);
(3)三次样条插值
p2 = spline(x,y,new_x); %三次样条插值
pp=csape(x0,y0) %计算插值函数
fnval(pp,x),fnder,fnint %分别计算返回值函数值,导数,积分
(4)n维插值
% n维数据的插值
x = -pi:pi; y = sin(x);
new_x = -pi:0.1:pi;
p = interpn (x, y, new_x, 'spline');
% 等价于 p = spline(x, y, new_x);
(5)Matlab实例
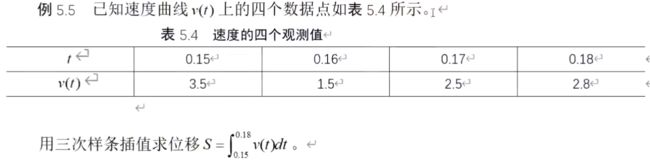
1.求位移
clc;clear;
format long g
t0=0.15:0.01:0.18;
v0=[3.5 1.5 2.5 2.8];
pp=csape(t0,v0) %三次样条插值函数
xishu=pp.coefs; %三次样条插值函数的系数
s1=integral(@(t)fnval(pp,t),0.15,0.18); %求积分(离散点数值积分)
format %恢复短小数据形式
2.求面积
clc;clear;close all;
a=importdata("data1.txt");
X0=a(1:3:end,:); X0=X0'; X0=X0(:); %逐列展开(转置后变成逐行展开)
y1=a(2:3:end,:); y1=y1'; y1=y1(:); %提出下边界的纵坐标
y2=a(3:3:end,:); y2=y2'; y2=y2(:); %提出上边界的纵坐标
plot(X0,y1,'*-');
hold on
plot(X0,y2,'.-');
pp1=csape(X0,y1);pp2=csape(X0,y2); %计算三次样条插值函数
dp1=fnder(pp1);dp2=fnder(pp2); %计算三次样条插值函数的导数
L1=integral(@(x)sqrt(1+fnval(dp1,x).^2)+sqrt(1+fnval(dp2,x).^2),X0(1),X0(end)); %计算弧长
L2=L1/18*40;
S1=integral(@(x)fnval(pp2,x)-fnval(pp1,x),X0(1),X0(end)); %计算面积
S2=S1/18^2*1600;
delta=(S2-41288)/41288;
%% 数值积分
%gradient 函数求导
L1=trapz(X0,sqrt(1+gradient(y1,X0).^2)); %计算下边界的长度
L2=trapz(X0,sqrt(1+gradient(y2,X0).^2)); %计算上边界的长度
L=L1+L2;
S=trapz(X0,y2-y1); %计算面积
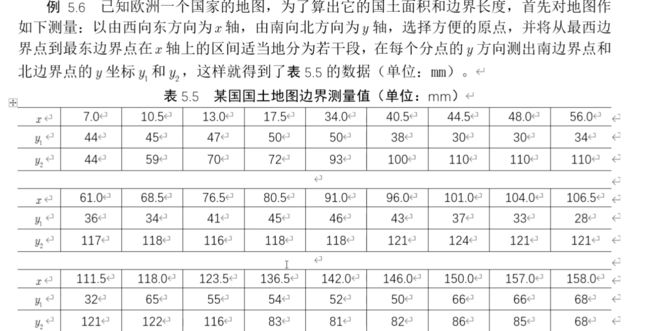
三.二维插值
1.概念
求近似的曲面函数,使其通过所有已知节点
2.二维插值方法
(1)网格节点法

1.最邻近点插值
取插值点函数为最邻近插值节点的函数值。最邻近点插值函数一般不连续。
2.分片线性插值
对应一维插值的分段线性插值,方法:将矩形区域分成两个三角形区域(插值函数连续)
在上三角区域内
(2)散乱数据插值法
四.Matlab实例
(1)二维插值函数
interp2(x0,y0,z0,x,y,'method');
csape({x,y},z);
五.拟合算法
1.概念
得到一个确定的曲线,尽管这条曲线不能保证经过每一个样本点,但只要保证误差足够小即可,这就是拟合思想
2.最小二乘法确定拟合曲线
clc;clear;
t=[0:7]';
y=[27.0 26.8 26.5 26.3 26.1 25.7 25.3 24.8]';
tb=mean(t);yb=mean(y);
ahat=sum((t-tb).*(y-yb))/sum((t-tb).^2); %最小二乘求系数
bhat=yb-ahat*tb;
a=[t,ones(8,1)];
cs=a\y; %矩阵除法
3.多项式拟合
% 法一
p=polyfity(x,y,n); %拟合n次多项式
y=polyfal(p,x); %计算多项式在x处的函数
% 法二
cftool %工具箱
% 法三
fit(x,y,'poly1') %拟合一次多项式
fit(x,y,'poly2') %拟合二次多项
4.黄河小浪底调水调沙问题
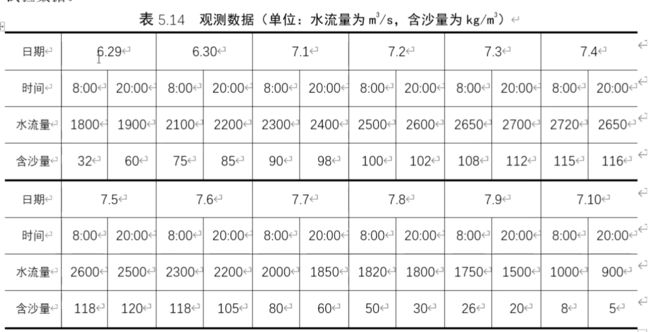

(1)问题求解:
转换成时刻:t=3600*(12i-4) (i=1,2,3,…)
排沙量=水流量*含沙量
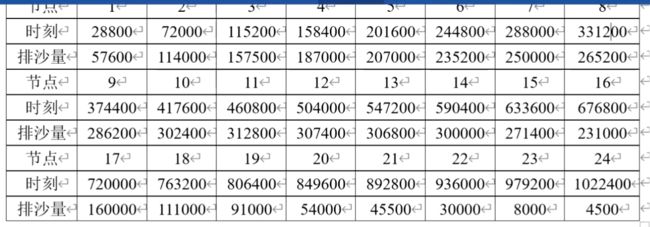
之后可通过插值或者拟合出函数关系.积分求解排沙量
clc,clear
format long g
load data3.txt %把表5.8中的日期和时间数据行删除,余下的数据保存在纯文本文件
liu=data3([1,3],:); liu=liu'; liu=liu(:); %提出水流量并按照顺序变成列向量
sha=data3([2,4],:); sha=sha'; sha=sha(:); %提出含沙量并按照顺序变成列向量
y=sha.*liu; y=y'; %计算排沙量,并变成行向量
i=1:24;
t=(12*i-4)*3600;
t1=t(1);t2=t(end);
pp=csape(t,y); %进行三次样条插值
xsh=pp.coefs %求得插值多项式的系数矩阵,每一行是一个区间上多项式的系数。
TL=integral(@(tt)fnval(pp,tt),t1,t2) %求总含沙量的积分运算
(2)问题求解
分成两个阶段,增长过程:到2720,到最大值之后为第二阶段
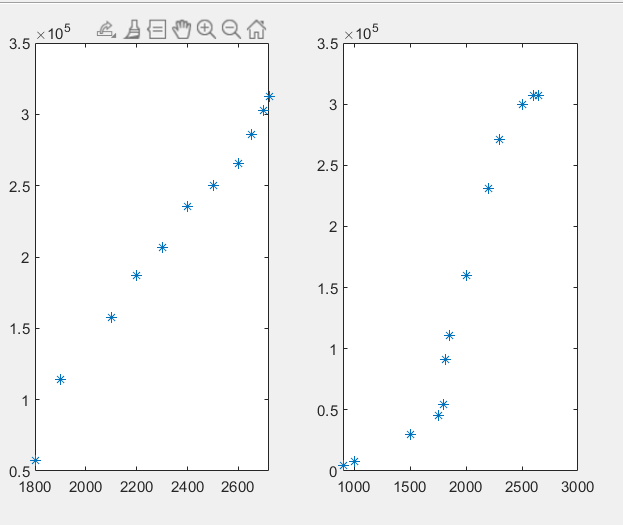
之后对两个阶段进行函数拟合
clc,clear
load data3.txt %把表5.8中的日期和时间数据行删除,余下的数据保存在纯文本文件
liu=data3([1,3],:); liu=liu'; liu=liu(:); %提出水流量并按照顺序变成列向量
sha=data3([2,4],:); sha=sha'; sha=sha(:); %提出含沙量并按照顺序变成列向量
y=sha.*liu; %计算排沙量,这里是列向量
subplot(1,2,1), plot(liu(1:11),y(1:11),'*')
subplot(1,2,2), plot(liu(12:24),y(12:24),'*')
format long e
%以下是第一阶段的拟合
for j=1:2
nihe1{j}=polyfit(liu(1:11),y(1:11),j);%拟合多项式,系数排列从高次幂到低次幂
yhat1{j}=polyval(nihe1{j},liu(1:11)); %求预测值
%以下求误差平方和与剩余标准差
cha1(j)=sum((y(1:11)-yhat1{j}).^2); rmse1(j)=sqrt(cha1(j)/(10-j));
end
celldisp(nihe1) %显示细胞数组的所有元素
rmse1
%以下是第二阶段的拟合
for j=1:2
nihe2{j}=polyfit(liu(12:24),y(12:24),j); %这里使用细胞数组
yhat2{j}=polyval(nihe2{j},liu(12:24));
rmse2(j)=sqrt(sum((y(12:24)-yhat2{j}).^2)/(12-j)); %求剩余标准差
end
celldisp(nihe2) %显示细胞数组的所有元素
rmse2
format %恢复默认的短小数的显示格式
%% 第二种方法(推荐)
for j=1:2
[ft1,st1]=fit(liu(1:11),y(1:11),['poly',int2str(j)])
xs=coeffvalues(ft1)
end
for j=1:2
[ft2,st2]=fit(liu(12:24),y(12:24),['poly',int2str(j)])
xs=coeffvalues(ft2)
end
结果
方法2
ft1 =
Linear model Poly1:
ft1(x) = p1*x + p2
Coefficients (with 95% confidence bounds):
p1 = 250.6 (228, 273.1)
p2 = -3.734e+05 (-4.269e+05, -3.199e+05)
st1 =
包含以下字段的 struct:
sse: 9.2062e+08
rsquare: 0.9860
dfe: 9
adjrsquare: 0.9844
rmse: 1.0114e+04
ft1 =
Linear model Poly2:
ft1(x) = p1*x^2 + p2*x + p3
Coefficients (with 95% confidence bounds):
p1 = -0.05824 (-0.1403, 0.02378)
p2 = 516.4 (141.4, 891.4)
p3 = -6.711e+05 (-1.093e+06, -2.488e+05)
st1 =
包含以下字段的 struct:
sse: 6.8954e+08
rsquare: 0.9895
dfe: 8
adjrsquare: 0.9869
rmse: 9.2840e+03
ft2 =
Linear model Poly1:
ft2(x) = p1*x + p2
Coefficients (with 95% confidence bounds):
p1 = 202.4 (149.8, 255.1)
p2 = -2.395e+05 (-3.441e+05, -1.349e+05)
st2 =
包含以下字段的 struct:
sse: 2.3191e+10
rsquare: 0.8668
dfe: 11
adjrsquare: 0.8547
rmse: 4.5916e+04
ft2 =
Linear model Poly2:
ft2(x) = p1*x^2 + p2*x + p3
Coefficients (with 95% confidence bounds):
p1 = 0.1067 (0.04357, 0.1697)
p2 = -180.5 (-409.8, 48.84)
p3 = 7.242e+04 (-1.254e+05, 2.703e+05)
st2 =
包含以下字段的 struct:
sse: 9.5867e+09
rsquare: 0.9449
dfe: 10
adjrsquare: 0.9339
rmse: 3.0962e+04