神经网络激活函数及参数初始化

1 激活函数（Activation functions）

1.1 sigmoid与tanh激活函数

使用一个神经网络时，需要决定使用哪种激活函数用隐藏层上，哪种用在输出节点上。

前面，我们在做神经网路的前向传播时，用[1] = ([1])和[2] = ([2])，这两步用到的是sigmoid函数。sigmoid 函数在这里被称为激活函数。

更通常的情况下，使用不同的函数([1])，除了可以是任何非线性函数，包括 sigmoid 函数。tanh 函数（双曲正切函数）是总体上都优于 sigmoid 函数的激活函数。

= ()的值域是位于+1 和-1 之间。

事实上，tanh 函数是 sigmoid 的向下平移和伸缩后的结果。对它进行了变形后，穿过了(0,0)点，并且值域介于+1 和-1 之间。

结果表明，如果在隐藏层上使用函数([1]) = ℎ([1]) 效果总是优于 sigmoid 函数。因为函数值域在-1 和+1的激活函数，其均值是更接近零均值的。在训练一个算法模型时，如果使用 tanh 函数代替sigmoid 函数中心化数据，使得数据的平均值更接近 0 而不是 0.5.

在进行优化算法时，有一点要说明：tanh 函数几乎在所有场合都优于 sigmoid 函数。只有一个例外：在二分类的问题中，对于输出层，因为的值是 0 或 1，所以想让^的数值介于 0 和 1 之间，而不是在-1 和+1 之间，需要使用 sigmoid 激活函数。

sigmoid 函数和 tanh 函数两者共同的缺点是，在特别大或者特别小的情况下，导数的梯度或者函数的斜率会变得特别小，最后就会接近于 0，导致梯度下降的速度降低。

1.2 ReLu 激活函数

在机器学习另一个很流行的函数是：修正线性单元的函数（ReLu）： = (0, ) 。只要是正值的情况下，导数恒等于 1，当是负值的时候，导数恒等于 0。

从实际上来说，当使用的导数时，=0 的导数是没有定义的。但是当编程实现的时候，的取值刚好等于 0.0000000，这个值相当小，所以，在实践中，不需要担心这个值，是等于 0 的时候，假设一个导数是 1 或者 0 效果都可以。

1.3 选择激活函数的经验法则

选择激活函数的经验法则是：如果输出是 0、1 值（二分类问题），则输出层选择 sigmoid 函数；如果是多分类，我们使用softmax激活函数；然后其它的所有单元都选择 Relu 函数。

这是很多激活函数的默认选择，如果在隐藏层上不确定使用哪个激活函数，那么通常会使用 Relu 激活函数。有时，也会使用 tanh 激活函数。

但 Relu 的一个特点是：当是负值的时候，导数等于 0。这里也有另一个版本的 Relu 被称为 Leaky Relu。 当是负值时，这个函数的值不是等于 0，而是轻微的倾斜，如图。这个函数通常比 Relu 激活函数效果要好，尽管在实际中 Leaky ReLu 使用的并不多。

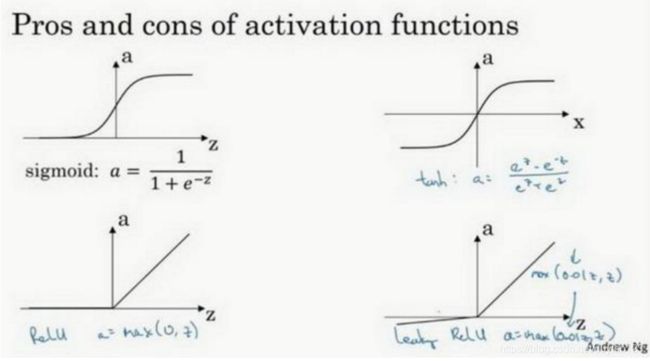
第一、使用 ReLu 激活函数神经网络通常会比使用 sigmoid 或者 tanh 激活函数学习的更快。

第二、sigmoid 和 tanh 函数的导数在正负饱和区的梯度都会接近于 0，这会造成梯度弥散，而 Relu 和 Leaky ReLu 函数大于 0 部分都为常熟，不会产生梯度弥散现象。(同时应该注意到的是，Relu 进入负半区的时候，梯度为 0，神经元此时不会训练，产生所谓的稀疏性，而 Leaky ReLu 不会有这问题)

第三、在 ReLu 的梯度一半都是 0，但是，有足够的隐藏层使得 z 值大于 0，所以对大多数的训练数据来说学习过程仍然可以很快。

1.4 总结

sigmoid 激活函数：除了输出层是一个二分类问题基本不会用它。

tanh 激活函数：tanh 是非常优秀的，几乎适合所有场合。

ReLu 激活函数：最常用的默认函数，如果不确定用哪个激活函数，就使用 ReLu 或者Leaky ReLu。

1.5 建议

在深度学习中的经常遇到一个问题：在编写神经网络的时候，会有很多选择：隐藏层单元的个数、激活函数的选择、初始化权值……这些选择想得到一个对比较好的指导原则是挺困难的。

由于神经网络的其特殊性和应用领域的不同，是很难提前知道选择哪些效果更好。所以通常的建议是：如果不确定哪一个激活函数效果更好，可以把它们都试试，然后在验证集或者测试集上进行评价。然后看哪一种表现的更好，就去使用它。

为自己的神经网络的应用尝试这些不同的选择，会在检验自己的神经网络或者评估算法的时候，看到不同的效果。如果仅仅遵守使用默认的 ReLu 激活函数，而不尝试使用其他的激励函数，那就可能在近期或者往后，每次解决问题的时候，都使用相同的办法，错过更好的模型表现。

---

2 为什么需要非线性激活函数？

为什么神经网络需要非线性激活函数？

事实证明：要让你的神经网络能够计算出有趣的函数，你必须使用非线性激活函数。

证明如下：

这是神经网络正向传播的方程，现在我们去掉函数，然后令[1] = [1]，或者我们也可以令() = ，这个有时被叫做线性激活函数（更学术点的名字是恒等激励函数，因为它们就是把输入值输出）。为了说明问题我们把[2] = [2]，那么这个模型的输出或仅仅只是输入特征的线性组合。如果我们改变前面的式子，令：

如果你是用线性激活函数或者恒等激励函数，那么神经网络只是把输入特征进行线性组合，然后再输出，即这样的神经网络实际上做的只是线性组合或者线性分类。

如果想用神经网络学习非线性分界面，你必须选择非线性激活函数。

我们稍后会谈到深度网络，有很多层的神经网络，很多隐藏层。事实证明，如果你使用线性激活函数或者没有使用一个激活函数，那么无论你的神经网络有多少层一直在做的只是计算线性函数，所以不如直接去掉全部隐藏层。

总而言之，不能在隐藏层用线性激活函数，可以用 ReLU 或者 tanh 或者 leaky ReLU 或者其他的非线性激活函数，唯一可以用线性激活函数的通常就是输出层；除了这种情况，会在隐层用线性函数的，除了一些特殊情况，比如与压缩有关的，那方面在这里将不深入讨论。在这之外，在隐层使用线性激活函数非常少见。因为房价都是非负数，我们也可以在输出层使用 ReLU 函数这样你的^都大于等于 0。

---

3 激活函数的导数（Derivatives of activation functions）

在神经网络中使用反向传播的时候，你需要计算激活函数的斜率或者导数。

针对以下四种激活，求其导数如下：

3.1 sigmoid activation function

3.2 Tanh activation function

3.3 Rectified Linear Unit (ReLU)

3.4 Leaky linear unit (Leaky ReLU)

---

4 随机初始化

4.1 为什么要做参数随机初始化？

当你训练神经网络时，权重随机初始化是很重要的。对于逻辑回归，把权重初始化为 0当然也是可以的。但是对于一个神经网络，如果你把权重或者参数都初始化为 0，那么梯度下降将不会起作用。让我们看看这是为什么。

有两个输入特征，[0] = 2，2 个隐藏层单元[1]就等于 2。 因此与一个隐藏层相关的矩阵，或者说[1]是 22 的矩阵，假设把它初始化为 0 的 22 矩阵，[1]也等于 [0 0]，把偏置项初始化为 0 是合理的，但是把初始化为 0 就有问题了。 那这个问题如果按照这样初始化的话，你总是会发现1[1] 和 2[1]相等，这个激活单元和这个激活单元就会一样。因为两个隐含单元计算同样的函数，当你做反向传播计算时，这会导致dz1[1] 和 dz2[1]也会一样，对称这些隐含单元会初始化得一样，这样输出的权值也会一模一样。

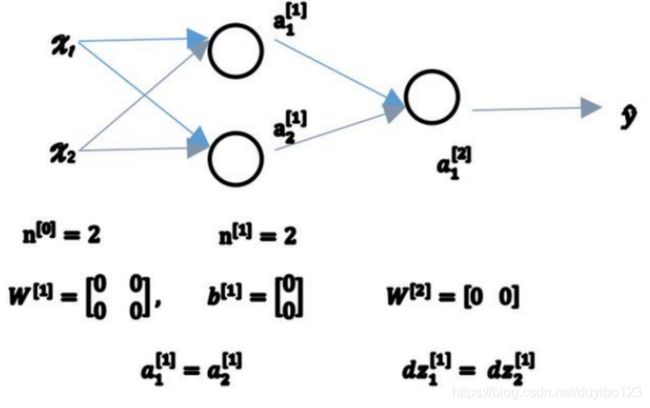
如果你这样初始化这个神经网络，那么这两个隐含单元就会完全一样，因此他们完全对称，会是一个这样的矩阵，每一行有同样的值因此我们做权重更新把权重[1] ⟹ [1] − 每次迭代后的[1]，第一行等于第二行，也就意味着计算同样的函数，并且肯定的是最终经过每次训练的迭代，这两个隐含单元仍然是同一个函数，令人困惑。

由此可以推导，如果你把权重都初始化为 0，那么由于隐含单元开始计算同一个函数，所有的隐含单元就会对输出单元有同样的影响。一次迭代后同样的表达式结果仍然是相同的，即隐含单元仍是对称的。通过推导，两次、三次、无论多少次迭代，不管你训练网络多长时间，隐含单元仍然计算的是同样的函数。因此这种情况下超过 1 个隐含单元也没什么意义，因为他们计算同样的东西。当然更大的网络，比如你有 3 个特征，还有相当多的隐含单元。

如果你要初始化成 0，由于所有的隐含单元都是对称的，无论你运行梯度下降多久，他们一直计算同样的函数。这没有任何帮助，因为你想要两个不同的隐含单元计算不同的函数，这个问题的解决方法就是随机初始化参 数 。

4.2 如何随机初始化？

你 应 该 这 么 做 ： 把 [1] 设 为np.random.randn(2,2)(生成高斯分布)，通常再乘上一个小的数，比如 0.01，这样把它初始化为很小的随机数。然后没有这个对称的问题，所以可以把 初始化为 0，因为只要随机初始化你就有不同的隐含单元计算不同的东西。相似的，对于[2]你可以随机初始化，[2]可以初始化为 0。

4.3 为什么是0.01？

你也许会疑惑，这个常数从哪里来，为什么是 0.01，而不是 100 或者 1000。我们通常倾向于初始化为很小的随机数。因为如果你用 tanh 或者 sigmoid 激活函数，或者说只在输出层有一个 Sigmoid，如果（数值）波动太大，当你计算激活值时[1] = [1] + [1] , [1] = ([1]) = 1如果很大，就会很大。的一些值就会很大或者很小，因此这种情况下你很可能停在 tanh/sigmoid 函数的平坦的地方(见图 3.8.2)，这些地方梯度很小也就意味着梯度下降会很慢，因此学习也就很慢。回顾一下：如果很大，那么你很可能最终停在（甚至在训练刚刚开始的时候）很大的值，这会造成 tanh/Sigmoid 激活函数饱和在龟速的学习上，如果你没有 sigmoid/tanh 激活函数在你整个的神经网络里，就不成问题。但如果你做二分类并且你的输出单元是 Sigmoid函数，那么你不会想让初始参数太大，因此这就是为什么乘上 0.01 或者其他一些小数是合理的尝试。对于[2]一样，就是 np.random.randn((1,2))，乘以0.01。

事实上有时有比 0.01 更好的常数，当你训练一个只有一层隐藏层的网络时（这是相对浅的神经网络，没有太多的隐藏层），设为 0.01 可能也可以。但当你训练一个非常非常深的神经网络，你可能会选择一个不同于的常数而不是 0.01。